Please refer to Class 12 Mathematics Sample Paper Term 1 Set F with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
CBSE Class 12 Mathematics Sample Paper for Term 1
Section A
In this section, attempt any 16 questions out of Questions 1-20. Each question is of 1 mark weightage.
1. If y = log x2 , then dy/dx at x = 2 is equal to
(a) 1
(b) 2
(c) 3
(d) 0
Answer
A
2. If A =
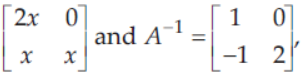
then 2x equals
(a) 2
(b) 1/2
(c) 1
(d) 1/2
Answer
C
3. The value of cos-1(cos 7π/6) is
(a) 7π/6
(b) π/6
(c) 5π/6
(d) None of these
Answer
C
4. The relation ‘has the same father as’ over the set of children is
(a) only reflexive
(b) only symmetric
(c) only transitive
(d) an equivalence relation
Answer
D
5. The elements aij of a 3 x 3 matrix are given by aij = 1/2 |-3i + j| , then 2/7 a32 is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
6. If y = 3e2x + e-x and d2y/dx2 – y = ke2x , then k is equal to
(a) 1
(b) 2
(c) 9
(d) 8
Answer
C
7. Consider the linear programming problem.
Maximise Z = x + 3y ; Subject to the constraints x + y ≤ 40, x + y ≤ 90 and x, y ≥ 0, then maximum value of Z is
(a) 0
(b) 50
(c) 90
(d) does not exists
Answer
A
8. The corner point of the feasible region determined by the system of linear constraints are (0, 0), (0, 20), (10, 20), (30, 10), (30, 0). The objective function is Z = 2x + 3y. Compare the quantity in Column A and Column B.

(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship cannot be determined on the basis of information supplied
Answer
A
9. If x = (t – 1)(t2+1+t) and y = (1-t)(1+t) , then dy/dx at t = -2/3 is equal to
(a) 0
(b) 5
(c) 1
(d) -2
Answer
C
10. If ay2 + bx2 + c = 0 , then dy/dx at (a, b) is equal to
(a) 2
(b) 3
(c) 0
(d) -1
Answer
D
11. If
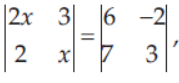
then the value of x2+1/2 is
(a) 10
(b) 20
(c) 15
(d) 1
Answer
A
12. The matrix

(a) diagonal matrix
(b) symmetric matrix
(c) skew-symmetric matrix
(d) scalar matrix
Answer
C
13. If A =
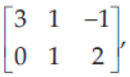
then AA’ is equal to

Answer
D
14. Let X = {0, 1, 2, 3, 4, 5} and Y = {-4, – 1, 0, 1, 4, 9, 16, 25} and f :X → Y defined by y = x2 , is
(a) one one onto
(b) one one into
(c) many one onto
(d) many one into
Answer
B
15. The function f : R → R given by f (x) = x3 + 1 is
(a) one-one but not onto
(b) onto but not one-one
(c) bijection
(d) neither one-one nor onto
Answer
C
16. If A =

then which of the following result is true
(a) A2 = I
(b) A2 = -I
(c) A2 = 2 I
(d) None of these
Answer
B
17. If Δ =

then Δ is equal to
(a) a2 + b2 + c2 + d2
(b) a2 – b2 – c2 – d2
(c) a2 – b2 + c2 – d2
(d) a2 – b2 – c2 +d2
Answer
A
18. Corner points of the feasible region for an LPP are : (0, 2), (3, 0), (6, 0) and (0, 5).
Let Z = 3x + 2y be the objective function. Then, MaximumZ -MinimumZ is equal to
(a) 20
(b) 16
(c) 14
(d) 18
Answer
C
19. The minimum value of y = x4 + 1 is
(a) 1
(b) 0
(c) – 1
(d) None of these
Answer
A
20. If A =
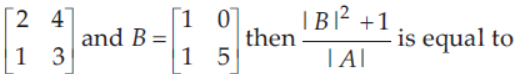
(a) 13
(b) 12
(c) 26
(d) 0
Answer
A
Section B
In this section, attempt any 16 questions out of Questions 21-40. Each question is of 1 mark weightage.
21. If y = √x2 + 1 + 1/√x+1 , then dy/dx at x = 1 is equal to
(a) 3/√2
(b) 3/4√2
(c) 4/3
(d) None of these
Answer
B
22. The feasible solution for a LPP is shown in following figure. Let Z = 3x + y be the objective function. Maximum of Z occurs at
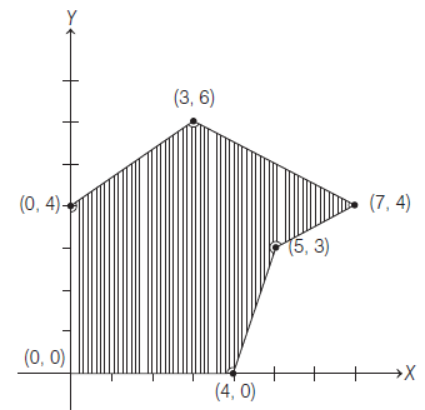
(a) (7, 4)
(b) (5, 3)
(c) (0, 4)
(d) (3, 6)
Answer
A
23. If matrix A =

and A2 = λ/2 A , then the value of λ is
(a) 12
(b) 10
(c) 11
(d) 14
Answer
A
24. The relation R defined on the set N of natural number xRy ⇔ 2x2 – 3xy + y2 = 0 is
(a) symmetric but not reflexive
(b) only symmetric
(c) not symmetric but reflexive
(d) None of these
Answer
C
25. If
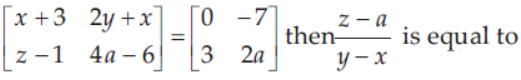
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
26. If A + B =

then B is equal to

Answer
A
27. If A =

then the value of|2A|- 4|A|is equal to
(a) – 1
(b) 2
(c) 1
(d) 0
Answer
D
28. The value of x for which matrix

is singular are
(a) 4, 1
(b) – 4, 1
(c) 2, 1
(d) None of these
Answer
B
29. If the points (0, 2), (1, x) and (3, 1) are collinear, then the value of x is
(a) 3/5
(b) 5/3
(c) 1
(d) 0
Answer
B
30. A and B are invertible matrices of the same order such that|(AB)-1 |= 8, if|A|= 2, then |B|is
(a) 16
(b) 4
(c) 6
(d) 1/16
Answer
D
31. If A =
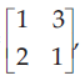
then the determinant value of A2 – 2A is
(a) 15
(b) 25
(c) 10
(d) 14
Answer
B
32. If A is a non-singular matrix of order 3 and|A|= – 8, then the value of|adj A|is
(a) – 8
(b) 64
(c) – 64
(d) 24
Answer
B
33. If A =
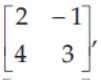
then A-1 is equal to

Answer
A
34. If the function f(x) =
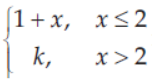
is continuous at x = 2, then the value of k is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
35. If y = log x, then d3y/dx3 is equal to
(a) 3/x2
(b) 2/x
(c) 2/x3
(d) 1
Answer
C
36. Let f(x) =
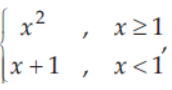
then at x = 1
(a) LHL = RHL
(b) LHL ≠ RHL
(c) LHL = f (1)
(d) None of these
Answer
B
37. Let f : R → R be a function such that f (x) = x3 + 3x2 + 5x + sin x , then f (x) is
(a) an increasing function
(b) decreasing function
(c) neither increasing nor decreasing function
(d) None of these
Answer
A
38. The function f (x) = log(cos x) on the interval (0,π/2) is
(a) Increasing
(b) Strictly decreasing
(c) Strictly increasing
(d) None of these
Answer
B
39. The slope of the normal to the curve y = 2x2 + 3x sin at x = 0 is
(a) 3
(b) 1/3
(c) – 3
(d) -1/3
Answer
D
40. The slope of the normal to the curve x = 1 – a sinq, y = b cos2 θ at θ = π/2 is
(a) a/2b
(b) -a/2b
(c) b/2a
(d) -b/2a
Answer
B
Section C
In this section, attempt any 8 questions. Each question is of 1 mark weightage. Questions 46-50 are based on Case-Study.
41. Let r be the relation on the set R of all real numbers defined by setting arb iff |a – b|≤ 1/2 .
Then, ρ is
(a) reflexive and symmetric but not transitive
(b) symmertic and transitive but not reflexive
(c) transitive but neither reflexive nor symmetric
(d) None of the above
Answer
A
42. If A2 + A + I = 0 then A-1 is equal to
(a) A- I
(b) I – A
(c) – (A+ I)
(d) None of these
Answer
C
43. If the function f(x) =
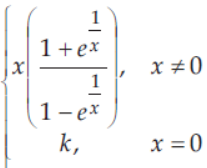
is continuous at x = 0, then the value of k is
(a) – 1
(b) 1
(c) 0
(d) 2
Answer
C
44. The function f (x) = 2x3 – 3x2 – 36x + 7 is strictly decreasing in the interval
(a) (- ∞, – 2)
(b) (- 2, 3)
(c) (3, ∞)
(d) None of these
Answer
B
45. The point on the curve y = (x – 3)2 , where the tangent is parallel to the chord joining (3, 0) and (4, 1) is
(a) (-7/2 , 1/4)
(b) (5/2 , 1/4)
(c) (-5/2 , 1/4)
(d) (7/2 , 1/4)
Answer
D
CASE STUDY
Ronit and Aman, two friends are standing on either side of a tower of 30 m high. They observe its top at the angle of elevation α and β respectively. (as shown in the figure below).
The distance between Ronit and Aman is 40√3 m and distance between Ronit and tower is 30 √3 m.
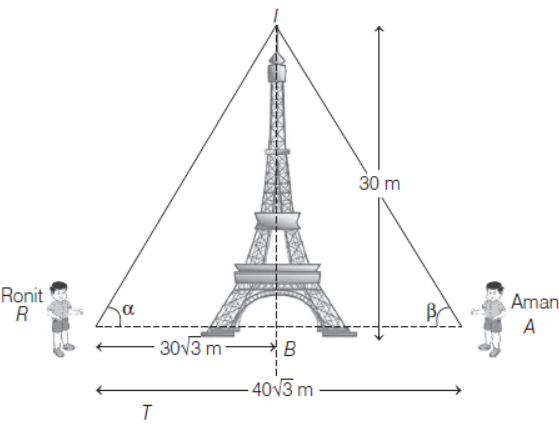
Based on the above information, answer the following questions.
46. ∠ART = α is equal to
(a) cos-1(4/5)
(b) cos-1(√3/2)
(c) cos-1(2/5)
(d) cos-1(1/5)
Answer
B
47. ∠ART = α is equal to
(a) sin-1(1/2)
(b) sin-1 2
(c) sin-1(√3/2)
(d) sin-1(2/√3)
Answer
A
48. ∠TAR = β is equal to
(a) tan-1(√3)
(b) tan-1(1/2)
(c) tan-1(2)
(d) tan-1(1/3)
Answer
A
49. ∠ATR is equal to
(a) π/2
(b) π/3
(c) π/4
(d) π/6
Answer
A
50. Domain and range of sin-1 x is
(a) [-1, 1],[-π/2 , π/2]
(b) [-1, 1], [0,π]
(c) [-1, 1], (-π/2 , π/2)
(d) (-1,1), (-π/2 , π/2)
Answer
A