VBQs Linear Inequalities Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Linear Inequalities Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Linear Inequalities VBQs Class 11 Mathematics
Question. The longest side of a triangle is 3 times the shortest side and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
(a) 2
(b) 9
(c) 8
(d) 7
Answer
B
Question. The graph of the solution on number line of the inequality 3x – 2 < 2x + 1 is

Answer
A
Question. Solution of |3x + 2| < 1 is
(a) [–1, –1/3]
(b) {–1/3,–1}
(c) (–1,–1/3)
(d) None of these
Answer
C
Question. If |x + 3| + x/x + 2 > 1, then x ∈
(a) (–5, –2)
(b) (–1, ∞)
(c) (–5, –2) ∪ (–1, ∞)
(d) None of these
Answer
C
Question. Let C/5 = F − 32/9 . If C lies between 10 and 20, then :
(a) 50 < F < 78
(b) 50 < F < 68
(c) 49 < F < 68
(d) 49 < F < 78
Answer
B
Question. The set of real values of x satisfying |x – 1| ≤ 3 and |x – 1| ≥ 1 is
(a) [2, 4]
(b) (−∞, 2]∪[4, +∞)
(c) [−2, 0]∪[2, 4]
(d) None of these
Answer
C
Question. If a < b and c < 0, then
(a) a/c = b/c
(b) a/c > b/c
(c) a/c < b/c
(d) None of these
Answer
B
Question. Linear inequalities for which the shaded region for the given figure is the solution set, are
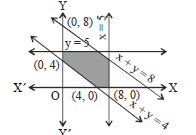
(a) x + y ≤ 8, x + y ≤ 4, x ≤ 5, y ≤ 5, x ≥ 0, y ≥ 0
(b) x + y ≤ 8, x + y ≥ 4, x ≤ 5, y ≤ 5, x ≥ 0, y ≥ 0
(c) x + y ≥ 8, x + y ≥ 4, x ≥ 5, y ≥ 5, x ≥ 0, y ≥ 0
(d) None of the above
Answer
B
Question. A manufacturer has 600 litres of a 12% solution of acid. How many litres of a 30% acid solution must be added to it so that acid content in the resulting mixture will be more than 15% but less than 18%?
(a) more than 120 litres but less than 300 litres
(b) more than 140 litres but less than 600 litres
(c) more than 100 litres but less than 280 litres
(d) more than 160 litres but less than 500 litres
Answer
A
Question. The solution set of 2x – 1/3 ≥ (3x – 2/4) – (2 – x/5) is (–∞, a]. The value of ‘a’ is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
A
Question. If x satisfies the inequations 2x – 7 < 11 and 3x + 4 < –5, then x lies in the interval (–∞, –m). The value of ‘m’ is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
B
Question. Ravi obtained 70 and 75 marks in first two unit tests. Then, the minimum marks he should get in the third test to have an average of at least 60 marks, are
(a) 45
(b) 35
(c) 25
(d) None of these
Answer
B
Question. Solution of a linear inequality in variable x is represented on number line is

(a) x ∈(−∞,5)
(b) x ∈(−∞,5]
(c) x ∈[5,∞)
(d) x ∈(5,∞)
Answer
D
Question. The graphical solution of 3x – 6 ≥ 0 is
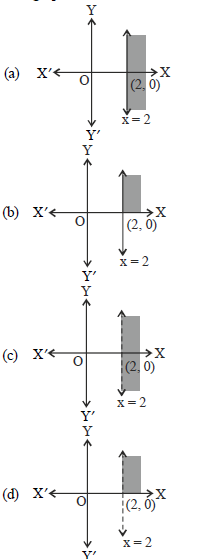
Answer
A
Question. If 3x–4/ ≥ x + 1/4– 1, then x ∈
(a) [1, ∞)
(b) (1, ∞)
(c) (–5, 5)
(d) [–5, 5]
Answer
A
Question. A furniture dealer deals in only two items — tables and chairs. He has Rs 15,000 to invest and a space to store atmost 60 pieces. A table costs him Rs 750 and chair Rs 150. Suppose he makes x tables and y chairs The graphical solution of the inequations representing the given data is
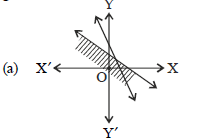
Answer
C
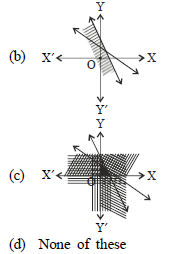
Question. Which of the following linear inequalities satisfy the shaded region of the given figure?
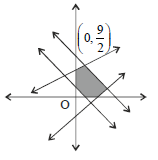
(a) 2x + 3y ≥ 3
(b) 3x + 4y ≤ 18
(c) x – 6y ≤ 3
(d) All of these
Answer
D
Question. The solution set of the inequality 4x + 3 < 6x + 7 is
(a) [–2, ∞)
(b) (–∞, –2)
(c) (–2, ∞)
(d) None of these
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
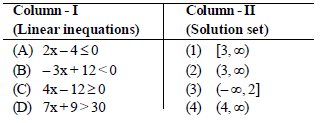
Codes
A B C D
(a) 3 4 1 2
(b) 3 1 4 2
(c) 2 4 1 3
(d) 2 1 4 3
Answer
A
Question. Which of the following is the solution set of linear inequalities 2(x – 1) < x + 5 and 3(x + 2) > 2 – x?
(a) (–∞, –1)
(b) (–1, 1)
(c) (–1, 7)
(d) (1, 7)
Answer
C
Question. The solutions of the system of inequalities 3x – 7 < 5 + x and 11 – 5x ≤ 1 on the number line is
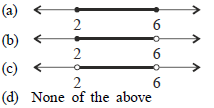
Answer
B
Question. A solution of 8% boric is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 L of the 8% solution, of the 2% solution will have to be added is
(a) more than 320 and less than 1000
(b) more than 160 and less than 320
(c) more than 320 and less than 1280
(d) more than 320 and less than 640
Answer
C
Question. If –3x + 17 < –13, then
(a) x ∈ (10, ∞)
(b) x ∈ [10, ∞)
(c) x ∈ (–∞, 10]
(d) x ∈ [–10, 10)
Answer
A
Question. The solution set of the inequality 37 – (3x + 5) ≥ 9x – 8 (x – 3) is
(a) (– ∞, 2)
(b) (– ∞, –2)
(c) (– ∞, 2]
(d) (– ∞, – 2]
Answer
C
Question. The inequality representing the following graph is

(a) |x| < 3
(b) |x| ≤ 3
(c) |x| > 3
(d) |x| ≥ 3
Answer
A
Question. A company manufactures cassettes. Its cost and revenue functions are C(x) = 26000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week. The number of cassettes must be sold by the company to realise some profit, is
(a) more than 2000
(b) less than 2000
(c) more than 1000
(d) less than 1000
Answer
A
Question. The solution set of the inequalities 3x – 7 > 2(x – 6) and 6 – x > 11 – 2x, is
(a) (–5, ∞)
(b) [5, ∞)
(c) (5, ∞)
(d) [–5, ∞)
Answer
C
Question. The inequality 2/x < 3 is true, when x belongs to
(a) [2/3,∞)
(b) (–∞,2/3]
(c) (–∞, 0) ∪ (2/3,∞)
(d) None of these
Answer
C
STATEMENT TYPE QUESTIONS
Question. Consider the following statements.
I. Solution set of 24x < 100 is {1, 2, 3, 4}, when x is a natural number.
II. Solution set of 24x < 100 is {…, –3, –2, –1, 0, 1, 2, 3, 4}, when x is an integer.
Choose the correct option.
(a) Only I is false.
(b) Only II is false.
(c) Both are false.
(d) Both are true.
Answer
D
Question. Consider the following statements.
I. Solution set of the inequality –15 < 3(x−2)/5 ≤ 0 is (–23, 2]
II. Solution set of the inequality 7 ≤ 3x + 11/2 ≤ 11 is [1,11/3]
III. Solution set of the inequality – 5 ≤ 2−3x/4 ≤ 9 is [–1, 1] ∪ [3, 5]
Choose the correct option
(a) Only I and II are true.
(b) Only II and III are true.
(c) Only I and III are true.
(d) All are true.
Answer
A
Question. Consider the following statements.
I. Equal numbers may be added to (or subtracted from)both sides of an inequality.
II. When both sides are multiplied (or divided) by a negative number, then the inequality is reversed.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both I and II are true.
(d) Both I and II are false.
Answer
C
Question. Consider the following statements:
Statement-I : The solution set of 7x + 3 < 5x + 9 is (–∞, 3).
Statement-II : The graph of the solution of above inequality is represented by
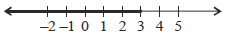
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
A
Question. Which of the following is/are true?
I. The graphical solution of the system of inequalities 3x + 2y ≤ 12, x ≥ 1, y ≥ 2 is
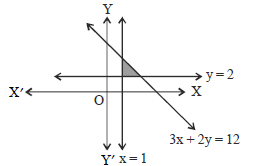
II. The region represented by the solution set of the inequalities 2x + y ≥ 6, 3x + 4y ≤ 12 is bounded.
III. The solution set of the inequalities x + y ≥ 4, 2x – y > 0 is
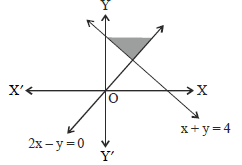
(a) Only I is true
(b) I and II are true
(c) I and III are true
(d) Only III is true
Answer
A
Question. Consider the following statements:
Statement-I : The solution set of the inequality 3(x – 2)/5 ≤ 5(2 – x)/3 is (–∞, 2).
Statement-II : The solution set of the inequality 1/2(13x/5 + 4) ≥ 1/3(x – 6) is (–∞, 120].
Choose the correct option.
(a) Statement I is true
(b) Statement II is true
(c) Both are true
(d) Both are false
Answer
B