Please refer to the Class 9 Mathematics Sample Paper for the current academic year given below. We have provided the latest CBSE Sample Papers for Term 1 and Term 2 for Mathematics Class 9. All guess sample papers have been prepared based on the latest blueprint and examination pattern for the current year. All sample papers for Mathematics Class 9 Term 1 and 2 have been given with solutions. Students can access the multiple guess papers given below. Practicing more Class 9 Mathematics Sample Papers will help you to get more marks in upcoming exams.
CBSE Sample Papers for Class 9 Mathematics
| Term 2 Sample Papers for Class 9 Mathematics |
| Class 9 Mathematics Sample Paper Term 2 Set A |
Class 9 Mathematics Sample Paper Term 2 Set A
Section – A
1. Factors of x4 – x2 – 12 are
(a) (x + 2), (x2– 2), (x2+ 3)
(b) (x + 3), (x – 3), (x2 + 2)
(c) (x + 2), (x – 2), (x2– 3)
(d) (x2+ 2), (x2– 6)
Answer
A
2. If (x – 1/x)2 = x2+ y + 1/x2 then the value of y is
(a) –2
(b) 2
(c) 2x
(d) –2x
Answer
A
3. x2+ (a + b + c)x + ab + bc =
(a) (x + a)(x + b + c)
(b) (x + a)(x + a + c)
(c) (x + b)(x + a + c)
(d) (x + b)(x + b + c)
Answer
C
4. Factorisation of a2x – b2x is
(a) (ax + bx)(ax – bx)
(b) (ax – bx)2
(c) (ax + bx)(ax – b2)
(d) (ax – bx)(ax + b2)
Answer
A
5. Which one of the following algebraic expressions is a polynomial in variable x ?
(a) x2 + 2/x2
(b) √x + 1/√x
(c) x2 + 3x3/2/√x
(d) None of these
Answer
C
6. If one factor of 5 + 8x – 4x2 is (2x + 1), then the second factor is
(a) (5 + 2x)
(b) (2x – 5)
(c) (5 – 2x)
(d) – (5 + 2x)
Answer
C
7. The two diagonals are equal in a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) trapezium
Answer
C
8. A quadrilateral has three acute angles each measuring 70°. The measure of fourth angle is
(a) 140°
(b) 150°
(c) 105°
(d) 120°
Answer
B
9. In a cyclic quadrilateral, the difference between two opposite angles is 58°, the measures of opposite angles are
(a) 158°, 22°
(b) 129°, 51°
(c) 109°, 71°
(d) 119°, 61°
Answer
D
10. Which of the following statements is true for a regular pentagon ?
(a) All vertices are con-cyclic.
(b) All vertices are not con-cyclic.
(c) Only four vertices are con-cyclic
(d) Cannot say anything about regular pentagon
Answer
A
11. Which of the following angles can be constructed by using ruler and compass only ?
(a) 20°
(b) 72°
(c) 105°
(d) 130°
Answer
C
12. The construction of a LMN in which LM = 8 cm, L = 45° is possible when (MN + LN) is
(a) 6 cm
(b) 7 cm
(c) 9 cm
(d) 5 cm
Answer
C
13. Vertical cross-section of a right circular cylinder is always a
(a) rectangle
(b) rhombus
(c) square
(d) trapezium
Answer
A
Assertion/Reason
In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
(a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) Assertion is true but Reason is false.
(d) Assertion is false but Reason is true.
14. Assertion : If f(x) = 3x7 – 4x6 + x + 9 is a polynomial, then its degree is 7.
Reason : Degree of a polynomial is the highest power of the variable in it.
Answer
A
15. Assertion : Two opposite angles of a parallelogram are (3x – 2°) and (50 – x)°. The measure of one of the angle is 37°.
Reason : Opposite angles of a parallelogram are equal.
Answer
A
16. Assertion : The length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm is 17.32 cm.
Reason : The perpendicular from the centre of a circle to a chord bisects the chord.
Answer
A
17. Assertion : The circumference of a circle must be a positive real number.
Reason : If r(> 0) is the radius of the circle, then its circumference 2 r is a positive real number.
Answer
A
18. Assertion : The external dimensions of a wooden box are 18 cm, 10 cm and 6 cm respectively and thickness of the wood is 15 mm, then the internal volume is 765 cm3.
Reason : If external dimensions of a rectangular box be l, b and h and the thickness of its sides
be x, then its internal volume is (l – 2x)(b – 2x)(h – 2x).
Answer
A
Match the Column
19. Column-II shows the degree of polynomials given Column-I
| Column-I | Column-II |
| (i) 2 – y2 – y3 + 2y8 | (1) 2 |
| (ii) 2 | (2) 1 |
| (iii) 5x – 7 | (3) 0 |
| (iv) 4 – x2 | (4) 8 |
(a) (i)-1,(ii)-3, (iii)- 2, (iv)- 4
(b) (i)-4, (ii)-3, (iii)- 2, (iv)- 1
(c) (i)- 4,(ii)-2, (iii)- 3, (iv)- 1
(d) (i)-2, (ii)- 3, (iii)- 4, (iv)- 1
Answer
B
20. Match the following :
| Column-I | Column-II |
| (i) Trapezium | (1) Each angle is 90° |
| (ii) Rectangle | (2) Equal adjacent sides but unequal opposite sides. |
| (iii) Rhombus | (3) Unequal sides. |
| (iv) Kite | (4) All sides are equal. |
(a) (i)- 1, (ii)- 2, (iii)- 3, (iv)- 4
(b) (i)- 2, (ii)- 3, (iii)- 4, (iv)- 1
(c) (i)- 4, (ii)- 3, (iii)- 2, (iv)- 1
(d) (i)- 3, (ii)- 1, (iii)- 4, (iv)- 2
Answer
D
Section – B
21. Degree of the polynomial p(x)= 3x4 + 6x + 7 is
(a) 4
(b) 5
(c) 3
(d) 1
Answer
A
22. If one factor of a(x + y + z) + bx + by + bz is (x + y + z), then the second factor is
(a) ax + ay + az
(b) bx + by + bz
(c) bx + by – bz
(d) a + b
Answer
D
23. Degree of the polynomial p(x) = (x + 2)(x – 2) is
(a) 2
(b) 1
(c) 0
(d) 3
Answer
A
24. If 8x4 – 8x2 + 7 is divided by 2x + 1, the remainder is
(a) 11/2
(b) 13/2
(c) 15/2
(d) 17/2
Answer
A
25. If a + b + c = 0, then a3 + b3 + c3 =
(a) abc
(b) 3abc
(c) 2abc
(d) – 3abc
Answer
B
26. For the polynomial p(x) = x5 + 4x3 – 5x2 + x – 1, one of the factors is
(a) (x + 1)
(b) (x – 1)
(c) x
(d) (x + 2)
Answer
B
27. A quadrilateral having only one pair of opposite sides parallel is called a
(a) square
(b) rhombus
(c) trapezium
(d) parallelogram
Answer
C
28. Two adjacent angles of a parallelogram are (2x + 25°) and (3x – 5)°. The value of x is
(a) 28°
(b) 32°
(c) 36°
(d) 42°
Answer
B
29. In a cyclic quadrilateral ABCD, if two sides are parallel, which of the following statements is definitely false ?
(a) Remaining two sides are equal
(b) Diagonals are not equal
(c) Diagonals intersect at the centre of circle
(d) Both (a) and (c)
Answer
B
30. To construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm. We draw line segment AB of 12 cm. Draw a ray AX making 90° with AB. The next step is :
(a) Cut a line segment AD of 18 cm on AX
(b) Cut a line segment BD of 18 cm
(c) Cut a line segment AD of 18 cm on AB
(d) Cut a line segment BD of 18 cm on AB
Answer
A
31. The ratio of the volume and surface area of a sphere of unit radius without considering units is
(a) 4 : 3
(b) 3 : 4
(c) 1 : 3
(d) 3 : 1
Answer
C
32. The number of surfaces in right cylinder is
(a) 4
(b) 3
(c) 2
(d) 1
Answer
B
33. A rectangular sheet of metal, x cm by y cm has a square of size z cm cut from each corner. The sheet is then bent to form a tray of depth z cm. The volume of the tray is
(a) z(x – z) (y – z) cm3
(b) xyz cm3
(c) z(x – 2z) (y – 2z) cm3
(d) (x + y)z cm3
Answer
C
Assertion/Reason
In each of the following questions, a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements, mark the correct answer as
(a) Both Assertion and Reason are true and Reason is the correct explanation of Assertion.
(b) Both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) Assertion is true but Reason is false.
(d) Assertion is false but Reason is true.
34. Assertion : (x + 2) and (x – 1) are factors of the polynomial x4 + x3 + 2x2 + 4x – 8.
Reason : For a polynomial p(x) of degree 1, x – a is a factor of the polynomial p(x) if and only if p(a) 1.
Answer
C
35. Assertion : The angles of a quadrilateral are x°, (x – 10)°, (x + 30)° and (2x)°, the smallest angle is equal to 58°.
Reason : Sum of the angles of a quadrilateral is 360°.
Answer
A
36. Assertion : If the diagonals of a parallelogram ABCD are equal, then ABC = 90°.
Reason : If the diagonals of a parallelogram are equal, it becomes a rectangle.
Answer
A
37. Assertion : The measure of AOC = 60°.
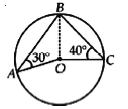
Reason : Angle subtended by an arc of a circle at the centre of the circle is double the angle subtended by arc on the circumference.
Answer
D
38. Assertion : A cone is a solid figure.
Reason : A cone is generated when rectangular sheet is rotated about its axis.
Answer
C
Match the Column
In the section, each question has two matching lists. Choices for the correct combination of elements from Column-I and Column-II are given as options (a), (b), (c) and (d) out of which one is correct.
39. By using a given figure of quadrilateral ABCD, match Column-I with Column-II.

| Column-I | Column-II |
| (i) If ABCD is a parallelogram, then sum of the angles x, y and z is | (1) 25° |
| (ii) If ABCD is a rhombus, where ∠D = 130°, then the value of x is | (2) 180° |
| (iii) If ABCD is a rhombus, the value of w is | (3) 50° |
| (iv) If ABCD is a parallelogram, where x + y = 130°, the value of z is | (4) 90° |
(a) (i)- 1, (ii)- 2, (iii)- 3, (iv)- 4
(b) (i)- 3, (ii)- 4, (iii)- 2, (iv)- 1
(c) (i)- 2, (ii)- 1, (iii)- 4, (iv)- 3
(d) (i)- 2, (ii)- 4, (iii)- 3, (iv)- 1
Answer
C
40. Match the following :
| Column-I | Column-II |
| (i) The radius of circle is 8 cm and the length of one of its chords is 12 cm. The distance of the chord from the centre is | (1) 23 cm |
| (ii) Two parallel chords of lengths 30 cm and 16 cm are drawn on the opposite sides of the centre of a circle of radius 17 cm. The distance between the chords is | (2) 5.196 cm |
| (iii) The length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm is | (3) 8.94 cm |
| (iv) An equilateral triangle of side 9 cm is inscribed in a circle.The radius of the circle is | (4) 8.94 cm |
(a) (i)- 3, (ii)- 1, (iii)- 4, (iv)- 2
(b) (i)- 3, (ii)- 4, (iii)- 1, (iv)- 2
(c) (i)- 1, (ii)- 2, (iii)- 3, (iv)- 4
(d) (i)- 1, (ii)- 3, (iii)- 2, (iv)- 4
Answer
A
Section – C
Case Study Based Questions
CASE STUDY-1 :
Mathematics teacher of a school took her 9th standard students to show Red fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students. Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the corners which are hemispherical. 7 smaller domes at the centre. Flag hoisting ceremony on Independence Day takes place near these domes.

41. How much cloth material will be required to cover 2 big domes each of radius 2.5 metres ? (Take π = 22/7)
(a) 75 m2
(b) 78.57 m2
(c) 87.47 m2
(d) 25.8 m2
Answer
B
42. Write the formula to find the volume of a cylindrical pillar :
(a) r2h
(b) rl
(c) l (l + r)
(d) 2 r
Answer
A
43. Find the lateral surface area of two pillars if height of the pillar is 7 m and radius of the base is 1.4 m.
(a) 112.3 cm2
(b) 123.2 m2
(c) 90 m2
(d) 345.2 cm2
Answer
B
44. How much is the volume of a hemisphere if the radius of the base is 3.5 m ?
(a) 85.9 m3
(b) 80 m3
(c) 98 m3
(d) 89.83 m3
Answer
D
45. What is the ratio of sum of volumes of two hemispheres of radius 1 cm each to the volume of a sphere of radius 2 cm ?
(a) 1 : 1
(b) 1 : 8
(c) 8 : 1
(d) 1 : 16
Answer
B
CASE STUDY-2 :
Aditi runs a handicraft shop in Bapu bazar in Jaipur. She makes beautiful necklaces using colourful beads which she keeps in a potli. Today she prepared 19 necklaces but could not make the 20th necklace as she had no yellow beads left. She counted the beads and found that there were 8 red, 6 green and 14 blue beads remaining in her potli. Her little daughter Dulari requested for a bead. Aditi decides to take out one bead from her potli for Dulari.
46. Find the probability that she draws a green bead.
(a) 3/11
(b) 3/7
(c) 11/14
(d) 3/14
Answer
D
47. Find the probability that the bead drawn by her is not green.
(a) 3/11
(b) 3/7
(c) 11/14
(d) 3/14
Answer
C
48. Find the probability that she draws either a green or a blue bead.
(a) 5/7
(b) 5/12
(c) 7/12
(d) 3/14
Answer
A
49. Find the probability that she draws neither a red nor a green bead.
(a) 3/14
(b) 1/3
(c) 3/7
(d) 1/2
Answer
D
50. Which of the following is an impossible event?
(a) The bead drawn is not red
(b) The bead drawn is neither red nor blue
(c) The bead drawn is either red or green or blue.
(d) The bead drawn is yellow.
Answer
D
