Please refer to the Class 10 Mathematics Sample Paper for the current academic year given below. We have provided the latest CBSE Sample Papers for Term 1 and Term 2 for Mathematics Class 10. All guess sample papers have been prepared based on the latest blueprint and examination pattern for the current year. All sample papers for Mathematics Class 10 Term 1 and 2 have been given with solutions. Students can access the multiple guess papers given below. Practicing more Class 10 Mathematics Sample Papers will help you to get more marks in upcoming exams.
CBSE Sample Papers for Class 10 Mathematics
| Term 2 Sample Papers for Class 10 Mathematics |
| Class 10 Mathematics Sample Paper Term 2 Set A |
Class 10 Mathematics Sample Paper Term 2 Set A
SECTION – A
1. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer : Let O be the common centre of two concentric circles and let AB be a chord of larger circle touching the smaller circle at P. Join OP.

Since OP is the radius of the smaller circle and AB is a tangent to this circle at P.
∴ OP ⊥ AB
Since perpendicular drawn from the centre of a circle to any chord of the circle bisects the chord.
⇒ AP = PB
Now, in ΔAOP, right-angled at P,
OA2 = AP2 + OP2 ⇒ 52 = AP2 + 32 ⇒ 25 – 9 = AP2
⇒ AP2 = 16 ⇒ AP = 4
Now AB = 2 × AP = 2 × 4 = 8 [∵ AP = PB]
Hence, the length of the chord of the larger circle which touches the smaller circle is 8 cm.
2. The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Answer : Let the two consecutive odd numbers be x and x + 2.
∴ x2 + (x + 2)2 = 394 ⇒ x2 + x2 + 4 + 4x = 394
⇒ 2x2 + 4x + 4 = 394 ⇒ 2x2 + 4x – 390 = 0
⇒ x2 + 2x – 195 = 0 ⇒ x2 + 15x – 13x – 195 = 0
⇒ x (x + 15) – 13 (x + 15) = 0 ⇒ (x – 13) (x + 15) = 0
Either x – 13 = 0 or x + 15 = 0 ⇒ x = 13 or x = – 15 (neglected)
When first number x = 13, then second number x + 2 = 13 + 2 = 15.
3. A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The height of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume inside the tent.
Answer : Let h1 = 4.2 m be the height of cylindrical portion, h2 = 2.1 m be the height of conical portion and r = 20 m be the radius of tent.
Then, the volume inside the tent = Volume of cylindrical part + Volume of conical part
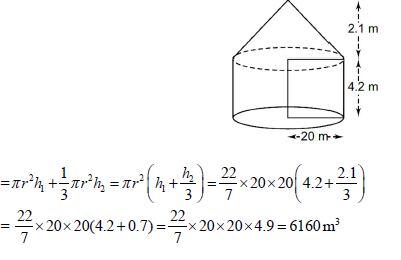
OR
A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Answer : Here, r = 3.5 cm
∴ h = (15.5 – 3.5) cm = 12.0 cm
Surface area of the conical part = πrl
Surface area of the hemispherical part = 2πr2
∴ Total surface area of the toy = πrl + 2πr2 = πr(l + 2r) cm2
Now, l2 = (12)2 + (3.5)2 = 156.25 cm2 ⇒ l = 12.5 cm
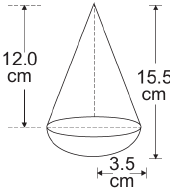
∴ TSA of the toy = 22/7 × 35/10 (12.5 2 3.5) = 11 × (12.5 + 7) cm2
= 11 × 19.5 cm2 = 214.5 cm2.
4. If the mean of the following distribution is 6.4, then find the value of ‘p’.

Answer :
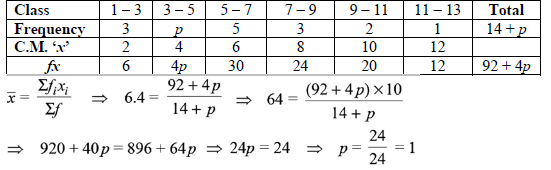
5. Find the sum of the given AP: – 5 + (– 8) + (– 11) + … + (– 230).
Answer : We have, a = – 5 and d = –8 + 5 = – 3
So, an = a + (n – 1)d
⇒ – 230 = – 5 + (n – 1) (– 3) ⇒ – 230 = – 5 – 3n + 3
⇒ – 230 + 2 = – 3n ⇒ – 228 = – 3n ⇒ n = 228/3 = 76

6. Solve the quadratic equation 2x2 + ax – a2 = 0 for x using quadratic formula.
Answer : Here, a = 2, b = a and c = –a2.
Using the formula,
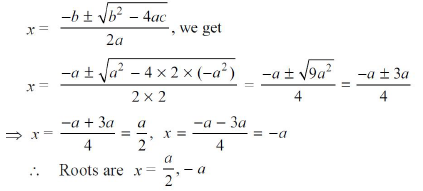
OR
If –5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots, then find the value of k.
Answer : Since, –5 is a root of the equation 2x2 + px – 15 = 0
∴ 2 (–5)2 + p (–5) – 15 = 0
⇒ 50 – 5p – 15 = 0 or 5p = 35 or p = 7
Again p (x2 + x) + k = 0 or 7x2 + 7x + k = 0 has equal roots
∴ D = 0 ⇒ b2 – 4ac = 0 or 49 – 4 × 7k = 0 ⇒ k = 49/28 = 7/4
SECTION – B
7. Calculate the mode for the following frequency distribution:

Answer : The frequency distribution table from the given data can be drawn as :

8. At a point on level ground, the angle of the elevation of the top of a vertical tower is found to be such that its tangent is 5/12. On walking 192 metres towards the tower, the tangent of the new angle of elevation is found to be. Find the height of the tower.
Answer : Let PQ be the tower of height h metres, point A be the first point of observation and B be the second point of observation towards the tower PQ such that AB = 192 m.
Also, let ∠PAQ = x and ∠PBQ = y

OR
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Answer : Let AB be the tower of height 30 m and CD be another tower of height h m.
Then, ∠ADB = 60° and ∠CBD = 30°

9. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Answer : Steps of construction:
1. Draw a circle with O as centre and radius as 3 cm.
2. Draw a diameter of it and extend both the sides and mark the points as P, Q such that OP = OQ = 7 cm.
3. Draw the perpendicular bisectors of OP and OQ to intersect PQ at M and N respectively.
4. With M as centre and OM as radius draw a circle to cut the given circle at A and B. With N as the centre and ON as radius draw a circle to cut the given circle at C and D.
5. Join PA, PB, QC, QD.
Hence, PA, PB and QC, QD are the required tangents from P and Q respectively.

10. If the median of the distribution given below is 28.5, then find the values of x and y.
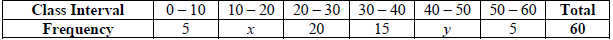
Answer :

SECTION – C
11. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each 5 mm of its ends (see along side). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its: (i) surface area (ii) volume
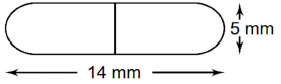
Answer : Since, diameter of the capsule = 5 mm, its radius = 5/2 mm = 2.5 mm
Length (height) of the cylindrical portion = 14 mm – 2 × 5/2 mm = 9 mm
(i) Surface area of the capsule
= Curved S.A. of its cylindrical part + 2 (curved S.A. of a hemispherical end)
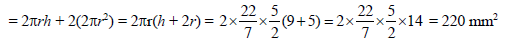
(ii) Volume of the capsule
= Volume of cylindrical part + 2 (volume of a hemispherical end)

12. In the given figure, OP is equal to diameter of the circle. Prove that ABP is an equilateral triangle.

Answer : Join OP and let it meets the circle at point Q.
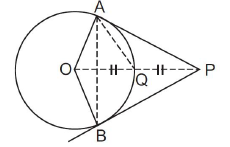
Since OP = 2r (Diameter of the circle)
⇒ OQ = QP = r
Consider ΔAOP in which OA ⊥ AP and OP is the hypotenuse.
∴ OQ = AQ = OA
(Mid-point of the hypotenuse is equidistant from the vertices)
⇒ OAQ is an equilateral triangle.
⇒ ∠AOQ = 60° (Each angle of an equilateral triangle is 60°)
Consider right-angled triangle OAP.
∠AOQ = 60° (Proved above)
∠OAP = 90° ⇒ ∠APO = 30°
∠APB = 2∠APO = 2 × 30° = 60°
Also PA = PB (Tangents to a circle from an external point are equal.)
⇒ ∠PAB = ∠PBA (Angles opposite to equal sides in ΔPAB)
In ΔABP, ∠APB = 60°
⇒ ∠PAB = ∠PBA = (180° − 60°)/2 = 60°
⇒ Each angle of ΔPAB is 60°
⇒ PAB is an equilateral triangle. Hence Proved.
OR
In the figure given, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠AOB = 90°.

Answer : Join O and C.

In ΔAOP and ΔAOC, OP = OC (Radii of a circle)
OA = OA (Common)
∠OPA = ∠OCA (Each 90°)
∴ ΔAOP ≅ ΔAOC (By RHS Congruency)
⇒ ∠1 = ∠2 …(i) (CPCT)
Similarly, ΔBOQ ≅ ΔBOC (By RHS Congruency)
⇒ ∠3 = ∠4 …(ii) (CPCT)
Now, ∠1 + ∠2 + ∠3 + ∠4 = 180° (Angles in a straight line)
⇒ 2∠2 + 2∠3 = 180° [From (i) and (ii)]
⇒ 2(∠2 + ∠3) = 180° ⇒ ∠2 + ∠3 = 90° ⇒ ∠AOB = 90°
CASE STUDY- 1
13. Mohan is watching the top of the lighthouse from the top of the building, he founds angle of elevation is 30° and then after he is watching the bottom of the lighthouse, he founds angle of depression is 60°. The height of the building is 60m. Based on this given information, answer the following questions.
(i) Find the difference between the heights of the lighthouse and the building.
(ii) Find the distance between the lighthouse and the building.
Answer :
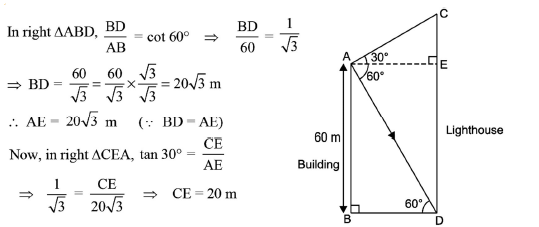
(i) Difference between the heights of the lighthouse and the building = CE = 20 m
(ii) The distance between the lighthouse and the building = BD = 20√3 m.
CASE STUDY- 2
14. Pollution – A Major Problem: One of the major serious problems that the world is facing today is the environmental pollution. Common types of pollution include light, noise, water and air pollution.

In a school, students thoughts of planting trees in and around the school to reduce noise pollution and air pollution.
Condition I: It was decided that the number of trees that each section of each class will plant be the same as the class in which they are studying, e.g. a section of class I will plant 1 tree, a section of class II will plant 2 trees and so on a section of class XII will plant 12 trees.
Condition II: It was decided that the number of trees that each section of each class will plant be the double of the class in which they are studying, e.g. a section of class I will plant 2 trees, a section of class II will plant 4 trees and so on a section of class XII will plant 24 trees.
(i) Refer to Condition I – If there are two sections of each class, how many trees will be planted by the students?
(ii) Refer to Condition II – If there are three sections of each class, how many trees will be planted by the students?
Answer : (i) Number of trees planted by the students of two sections of class I = 1 × 2 = 2
Number of trees planted by the students of two sections of class II = 2 × 2 = 4
Similarly, Number of trees planted by the students of two sections of class III = 3 × 2 = 6
Number of trees planted by the students of two sections of class XII = 12 × 2 = 24
So, the number of trees planted by the students of two sections of different classes are 2, 4, 6, ……24
This series forms an AP
Here,first term(a) = 4, common Difference (d) = 4 – 2 = 2, last term (l) = 24 and (number of terms)n = 12
Number of trees planted by the students =sum of 12 terms of above AP
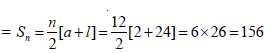
(ii) Number of trees planted by the students of two sections of class I = 2 × 3 = 6
Number of trees planted by the students of two sections of class II = 4 × 3 = 12
Similarly, Number of trees planted by the students of two sections of class III = 6 × 3 = 18
Number of trees planted by the students of two sections of class XII = 24 × 3 = 72
So, the number of trees planted by the students of two sections of different classes are 6, 12, 18, ……,72
This series forms an AP
Here, first term(a) = 6, common Difference (d) = 12 – 6 = 6, last term (l) = 72 and (number of terms)n = 12
Number of trees planted by the students = sum of 12 terms of above AP


