Please refer to the Class 12 Mathematics Sample Paper for the current academic year given below. We have provided the latest CBSE Sample Papers for Term 1 and Term 2 for Mathematics Class 12. All guess sample papers have been prepared based on the latest blueprint and examination pattern for the current year. All sample papers for Mathematics Class 12 Term 1 and 2 have been given with solutions. Students can access the multiple guess papers given below. Practicing more Class 12 Mathematics Sample Papers will help you to get more marks in upcoming exams.
CBSE Sample Papers for Class 12 Mathematics
Class 12 Mathematics Sample Paper Term 2 Set A
Section – A
1. Evaluate :∫01 x(1-x)ndx
OR
Evaluate : ∫sin3 x cos3 x dx
Answer: Using

OR

2. Determine the sum of order and degree of the given differential equation.
(y′′′)2 + (y′′)3 + (y′)4 + y5 = 0.
Answer: The given differential equation is (y””)2+(y”)3=(y)4+y5=0
The highest order derivative present in the differential equation is y′′′. Therefore, its order is three.
The given differential equation is a polynomial equation in y′′′, y′′ and y′.
∴ The highest power raised to y′′′ is 2.
Hence, its degree is 2.
Now, we know order is 3 and degree is 2.
So, Sum of order and degree of given differential equation is 3 + 2 = 5.
3. Write a vector of magnitude 15 units in the direction of vector î -2ĵ +2k̂
Answer:

4. If the line has the direction ratio – 18, 12, – 4, then what are its direction consines?
Answer: The direction ratios of the lines are – 18, 12, – 4 Direction cosines of the lines are
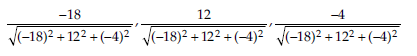

Hence, direction cosines of line are −9 −11, 6/11,-2/11 ·
5. Mother, father and son line up at random for a family photos. If A and B are two events given by A = Son on one end, B = Father in the middle, find P(B/A).
Answer: If mother (M), father (F), and son (S) lineup for the family picture, then the sample space will be
S = (MFS, MSF, FMS, FSM, SMF, SFM)
∴ A = (MFS, FMS, SMF, SFM),
B = (MFS, SFM)
And A ∩ B = (MFS, SFM)
∴ P(A ∩ B) =2/6= 1/3,
P(B) =2/6=1/3,
p(A)=4/6=2/3
p(B/A)=P(A∩ B)/P(A)=1/3/2/3=1/2
⇒ P(B/A) =1/2
6. A coin is tossed 5 times. Find the probability of getting (i) at least 4 heads, and (ii) at most 4 heads.
Answer: Total number of probability of tossing a coin 5 times is 32
(i) Probability of getting atleast 4 heads.
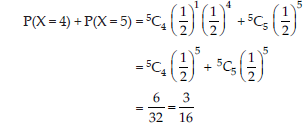
(ii) Probability of getting at most 4 heads
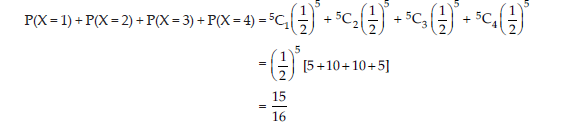
Section – B
7. Evaluate: ∫ x sin x dx.
Answer: Let, Using integration by parts,
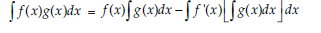
So, we take
So,
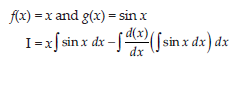

8. Solve the differential equation
dy/dx= 1 + x + y2 + xy2, if y = 0 when x = 0
OR
Solve the differential equation:
x log x dy/dx+ y = 2 log x.
Answer: Given differential equation is,

OR

9. If →a= 2 →i +4 ĵ- 5 k̂ and →b = î,+ 2ĵ,+3k̂ , find the unit vector in the direction →a →b.
Answer: We have,

Hence, the unit vector in the direction of →a+ →b

10. Find the foot of perpendicular from the point (1, 6, 3) on the line;
x = y − 1/2= z − 2/2
OR
If vector →a=2 î +2ĵ+3k̂,→b=-î+2ĵ+k̂ and →c=3î+ĵ are such that →a +λ→b
is perpendicular to→c, then find the value of λ.
Answer: Given line is,
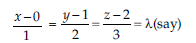
It can be written as
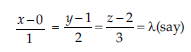
So, x = λ, y = 2λ + 1 and z = 3λ + 2.
∴ Coordinates of any general point which lines on the given line are (l, 2l + 1, 3λ + 2).
∴ Coordinates of foot of perpendicular are (λ, 2λ + 1, 3λ + 2).
Now, direction ratios of line joining (1, 6, 3) and foot of perpendicular (λ 2λ + 1, 3λ + 2) will be,
λ– 1, 2λ + 1 – 6, 3λ+ 2 – 3 = λ – 1, 2λ – 5, 3λ – 1.
Also, direction ratios of given line are 1, 2, 3.
Since, line joining (1, 6, 3) and foot of perpendicular is perpendicular to given line


Section – C
11. Evaluate : ∫0 π/4 log (1+ tanx )dx .
Answer:

12. Find the area of region bounded by the curve y2 = 2y – x and the Y – axis.
OR
Find the area of region bounded by the curves:
x2 = y and y = |x|.
Answer:


OR

13. Find the shortest distance between the lines
→ r1= 3 î +2 ĵ -4 k̂ +λ (î +2 ĵ + 2k̂ )
→ r1= 5 î -2 j+μ 3 î 2 ĵ+ 6 k̂
and If the line intersect find their point of intersection.
Answer:


14. A glass jar contains twenty white balls of plastic numbered from 1 to 20, ten red balls of plastic numbered from 1 to 10, forty yellow balls of plastic numbered from 1 to 40 and ten blue balls of plastic numbered from 1 to 10. If these 80 balls of plastic are thoroughly shuffled so that each ball has the same probability of being drawn.

Based on the above information answer the following:
(i) Determine the probabilities of drawing a ball of plastic that is red or yellow and numbered 1, 2, 3
or 4.
(ii) Discuss the probabilities of drawing a plastic ball which is numbered 5, 15, 25 or 35.
Answer: As we have given;
Total number of balls in jar = 80
20 white balls of numbered 1 to 20
i.e., 1 white ball contains one number,
10 Red balls of numbered 1 to 10
i.e., 1 Red ball contains one number,
Similarly, Yellow ball contains one number per ball and
Blue ball contains one number per ball.
(i) Number of Red balls of numbered 1, 2, 3, and 4 = 4
Number of Yellow balls of numbered 1, 2, 3 and 4 = 4
P(Red or yellow and numbered 1, 2, 3 or 4) = P(Red numbered 1, 2, 3 or 4) + P(Yellow numbered 1,2, 3 or 4)
=4/80+4/80
= 8/80
= 1/10
(ii) Number of White balls of numbered 5, 15 = 2,
Number of Red balls of numbered 5 = 1,
Number of Yellow balls of numbered 5, 15, 25 and 35 = 4,
Number of Blue balls of numbered 5 = 1
P(numbered 5, 15, 25 or 35) = P(5) + P(15) + P(25) + P(35)
= P(White) + P(Red) + P(Yellow) + P(Blue)
=2/80+1/80+4/80+1/80
=8/80
=1/10
