Please refer to Class 12 Mathematics Sample Paper Set H with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
SECTION – A
1. Evaluate x if
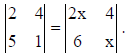
Solution: Here
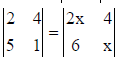
⇒ 2 – 20 = 2x2 – 24 ⇒ x2 = 3 ∴ x = ±√3 .
2. If matrix A= [aij]2×2 where aij =
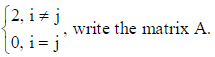
write the matrix A.
Solution:

3.
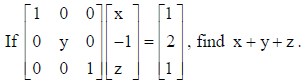
Solution:
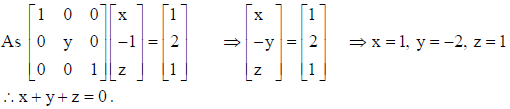
4. If a̅ and b̅ denote the position vectors of points A and B respectively and C is a point on AB such that AC = 2CB, then write the position vector of C.
Solution: Clearly here C divides AB in 2 : 1 so, position vector of C = 2b̅ + a̅/3 .
5. For vector a̅ if |a̅| = a , then write the value of (a̅ x î)2 + (a̅ x ĵ)2 + (a̅ x k̂)2 .
Solution: Let a̅ makes α , β , γ angles with î , ĵ and k̂ respectively.
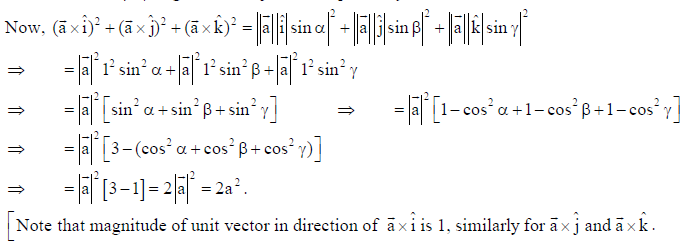
6. A line passes through the point with position vector 2î – 3ĵ + 4k̂and makes angles 60o , 120o and 45o with x, y and z-axis respectively. Find the equation of the line in the Cartesian form.
Solution: As the line makes angles 60o , 120o and 45o with x, y and z-axis respectively so, its d.c.’s are
cos60o , cos120o , cos 45o i.e., 1/2 , -1/2 , 1/√2 .
So equation of line through the point with the position vector 2î – 3ĵ + 4k̂, is
x-2/1/2 = y+3/-1/2 = z-4/1/2 or, 2x – 4 = -2y – 6 = √2 z – 4 √2 .
SECTION – B
7. If tan-1 (x-2/x-1) + tan-1(x+2/x+1) = π/4 , then find the value of x.
Solution:

OR
Prove that tan-1 {√1+cos x + √1-cos x/√1+cos x – 1-cos x} = π/4 + π/2 , if 0 < x < π/2 .
Solution:

8. To raise money for an orphanage, students of three schools A, B and C organized an exhibition in their locality, where they sold paper bags, scrap-books and pastel-sheets made by them using recycled paper at the rate of ₹ 20, ₹ 15 and ₹ 10 per unit respectively. School A sold 25 paper bags, 10 scrap-books and 30 pastel-sheets. School B sold 20 paper bags, 15 scrap-books and 30 pastel-sheets. While school C sold 25 paper bags, 18 scrap-books and 35 pastel-sheets. Using matrices, find the total amount raised by each school. By such exhibition, which values are inculcated in the students?
Solution: Let ₹ x, ₹ y and ₹ z be raised by the schools A, B and C respectively.

By equality of matrices, we get : x = 950, y = 925, z = 1120 .
Value : Helping nature.
9. If y = ae2x + be-x , show that d2y/dx2 – dy/dx – 2y = 0 .
Solution:

OR
Differentiate x (sin x – cos x) + x2-1/x2+1 with respect to x.
Solution:
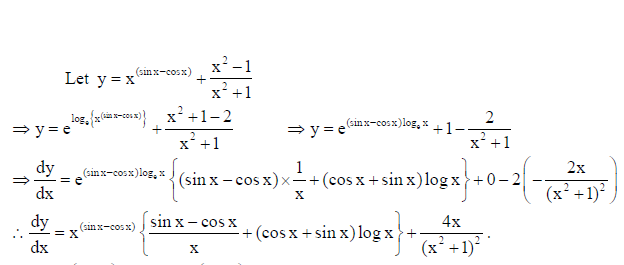
10. If x = a(t + 1/t) and y = a (t-1/t) , prove that dy/dx = x/y .
Solution: Here x = a (t + 1/t) and y = a (t-1/t) ⇒ dy/dx = a(1-1/t2) and dy/dt = a (1+1/t2)
∴ dy/dx = dy/dx x dt/dx = a (1+1/t2)/a(1-1/t2) = at (1+1/t2/at (1-1/t2) = a (t+1/t)/a (t-1/t) = x/y .
11. Find the points on the curve y = x3 – 3x2 – 9x + 7 at which the tangent to the curve is parallel to the x-axis.
Solution: As the tangents to the curve y = x3 – 3x2 – 9x + 7 are parallel to x-axis so, dy/dx = 3x2 – 6x – 9 = 0
⇒ 3(x2 – 2x -3) = 0 ⇒ x = 3,=1
Hence the required points are (3,-20) and (-1,12) .
12. Find : ∫x sin-1 x dx .
Solution: Let I = ∫x sin-1 x dx ⇒ I = sin-1 x ∫xdx – ∫(d/dx sin-1 x ∫xdx) dx
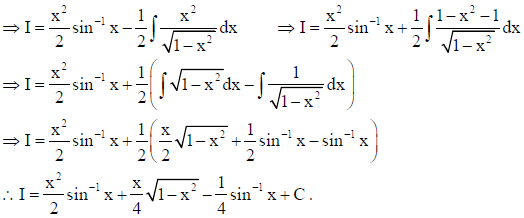
13. Find :
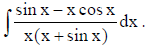
Solution:
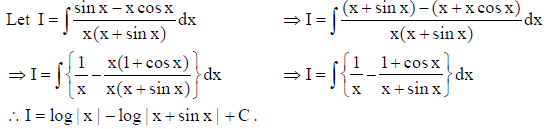
14. Evaluate :
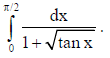
Solution:

OR
Evaluate :
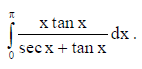
Solution:
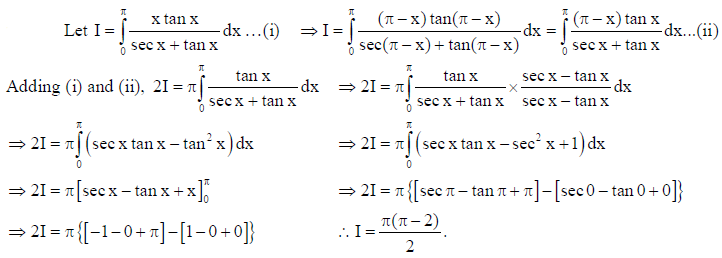
15. Find the general solution of the differential equation : xdy – ydx = √x2 + y2 dx .
Solution:
16. Solve (1+x2) dy/dx + 2xy – 4x2 = 0 subject to the initial condition y(0) = 0.
Solution: Here (1+x2) dy/dx + 2xy – 4x2 = 0 ⇒ dy/dx + 2x/1+x2 y = 4x2/1+x2
It is of the form dy/dx + P(x)y = Q(x) , where P(x) = 2x/1+x2 , Q(x) = 4x2/1+x2
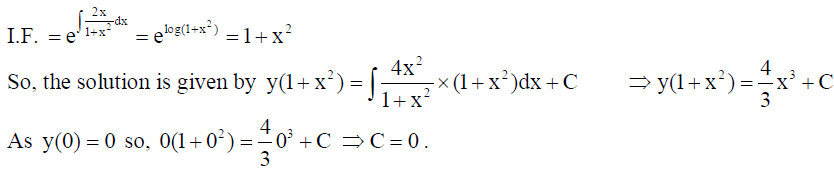
Therefore the required solution is y = 4x3/3(1+x2)
17. Find a unit vector perpendicular to both of the vectors 3a̅ + 2b̅ and 3a̅ – 2b̅ , where a̅ = î + ĵ + k̂, b̅ = î + 2ĵ + 3k̂ .
Solution: Here 3a̅ + 2b̅ = 5î + 7ĵ + 9k̂ , 3a̅ – 2b̅ = î – ĵ – 3ĵ
Let r̅ be perpendicular to the vectors 3a̅ + 2b̅ and 3a̅ – 2b̅ .
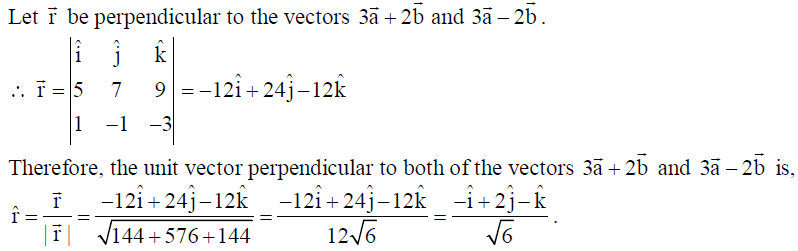
18. Find the shortest distance between the lines :
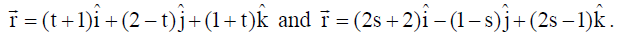
Solution:
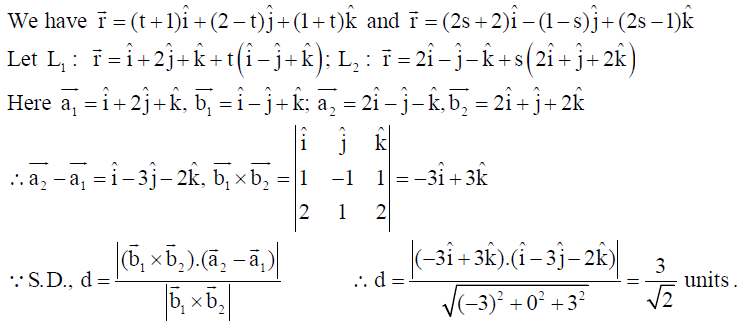
19. From a lot of 30 bulbs which includes 6 defectives, a sample of 4 bulbs is drawn at random one by one with replacement. Find the probability distribution of the number of defective bulbs. Hence find the mean of the distribution.
Solution: Let X : Number of defective bulbs out of 4 bulbs drawn with replacement.
So, X = 0, 1, 2, 4.
Here p = probability of getting defective bulbs = 6/30 = 1/5 , q = 4/5 .
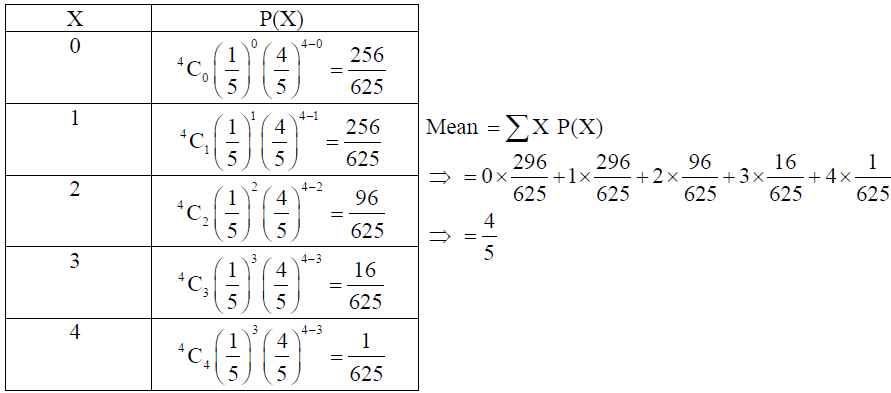
OR
A and B threw a pair of dice alternatively. A wins the game if he gets a total of 9 and B wins if he gets a total of 7. If A starts the game, find the probability of winning the game in by B.
Solution: Let X be the event of getting a total of 9 and Y be the event of getting a total of 7.
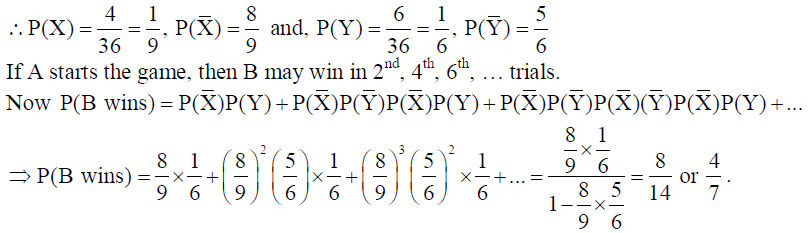
SECTION – C
20. Show that the function f : R → {x ∈ R : -1< x <1} defined by f (x) = x/1+|x| , x ∈ R is one-one and onto function. Hence find f -1(x) .
Solution: Here f : R → {x ∈ R : -1< x <1} is defined by f(x) = x/1+|x| , x ∈ R
One-one : Let 1 2x , x ∈ R so that f(x1) = f(x2) ⇒ x1/1+|x1| = x2/1+|x2|
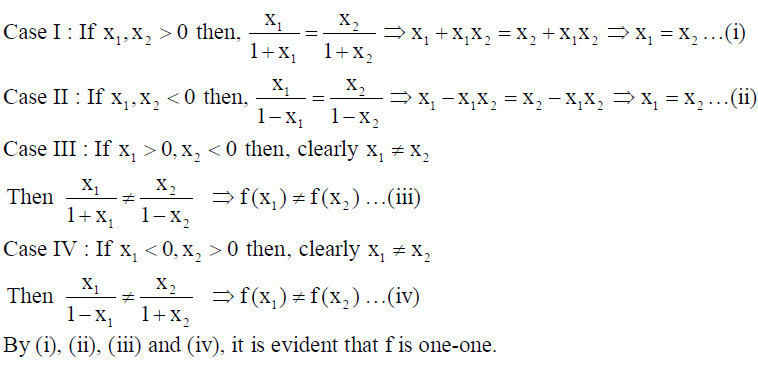
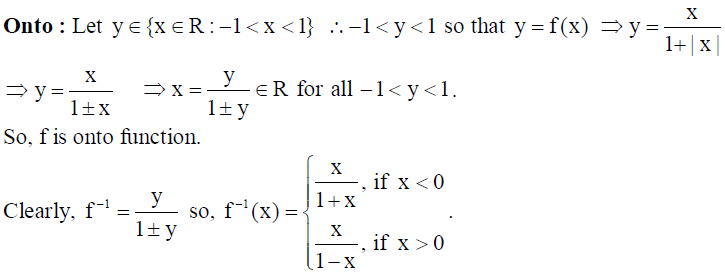
21. Using properties of determinants, prove that
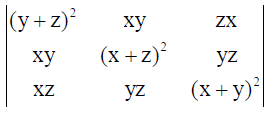
= 2xyz(x + y + z)3 .
Solution:

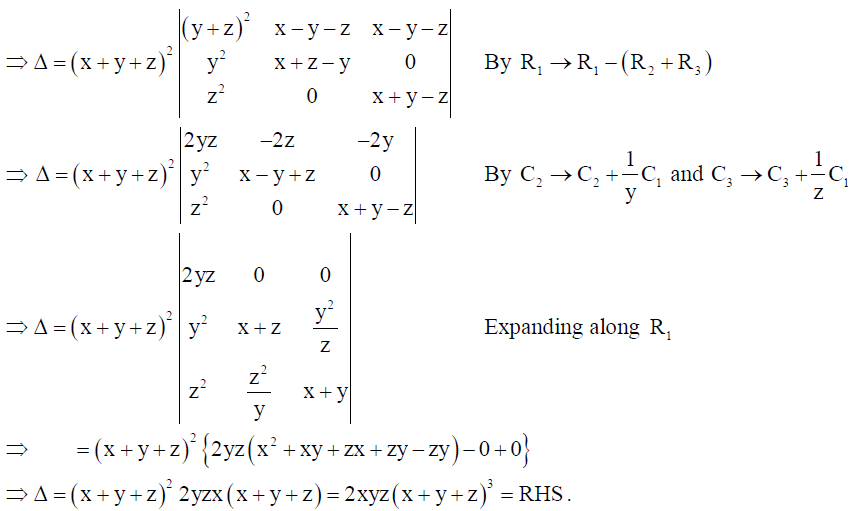
OR
If

prove that A3 – 6A2 + 7A + 2I = O .
Solution:

22. A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs ` 5 per cm2 and the material for the sides costs ` 2.50/cm2. Find the least cost of the box.
Solution: Let side of square base of box be x cm and its height be h cm.
Volume of the box = 1024 cm3
⇒ x.x.h =1024 ∴ h = 1024/x2
Now cost of the box, C = 5 x 2x2 + 2.5 x 4xh = 10x2 10hx 10x2 + 10240/x
⇒ dC/dx = 20x – 10240/x2 , d2C/dx2 = 20 + 20280/x3
For the local points of maxima and/or minima,
dC/dx = 20x – 20240/x2 = 0
⇒ x3 = 512 ∴ x = 8 cm
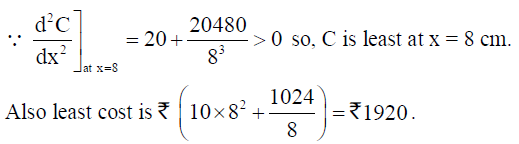
OR
Show that the altitude of a right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3.
Solution: Let ABC be a cone of maximum volume inscribed in a sphere of radius r.
Let BD = x. In ΔOBD, OD2 + BD2 = OB2
∴ (h – r)2 + x2 = r2 ⇒ x2 = r2 – (h – r)2
Then volume of cone, V = 1/3 π (BD)2 (AD)
⇒ V = 1/3 π(x2)(h) ∴ V = π/3(2hr h2 )(h)
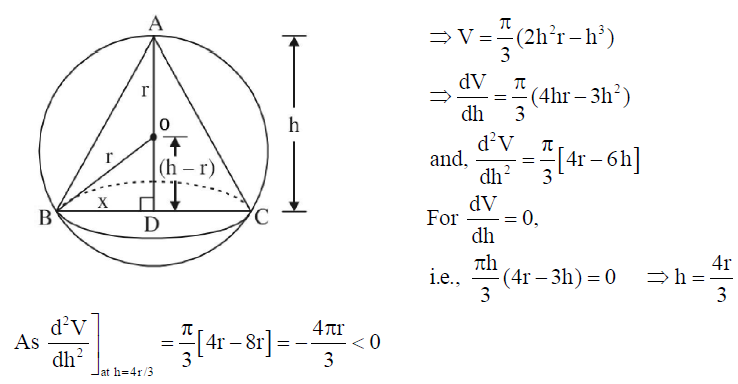
So, V is maximum at h = 4r/3 .
Therefore, the altitude of a right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3.
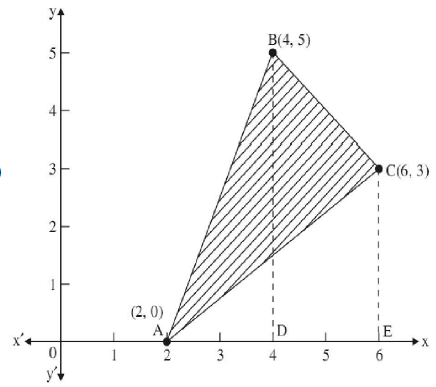
23. Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B(4, 5) and C(6, 3).
Solution: Equation of side AB : y = 5/2 (x-2)
Equation of side AC : y = 3/4(x-2)
Equation of side BC : y = 9- x .
Now ar(ABC) = ar(ABD) + ar(BCED) – ar(ACE)
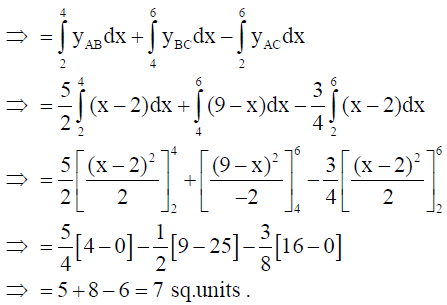
24. Find the vector and Cartesian equations of the plane passing through the point (–1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
Solution: Let the d.r.’s of the normal to the plane passing through the point (–1, 3, 2) be A, B, C.
So, eq. of plane is : A(x +1) + B(y – 3) + C(z – 2) = 0…(i)
As (i) is perpendicular to the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.
So, A + 2B + 3C = 0…(ii) and, 3A + 3B + C = 0…(iii)
Solving (ii) and (iii), we get : A/2-9 = B/9-1 = C/3-6 i.e., A/-7 = B/8 = C/-3 i.e., the d.r.’s are –7, 8, –3.
By (i), -7(x +1) + 8(y – 3) – 3(z – 2) = 0 i.e., 7x – 8y + 3z + 25 = 0 , which is Cartesian equation.
Also the vector equation of plane is, r̅ .(7î – 8ĵ + 3k̂) + 25 = 0
25. A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random (without replacement) from the bag which are both found to be red. Find the probability that the balls are drawn from the first bag.
Solution: Let E1 : event of selecting bag with 4 red and 4 black balls and, E2 : event of selecting bag with 2 red and 6 black balls.
Also let E : event of selecting 2 red balls without replacement.
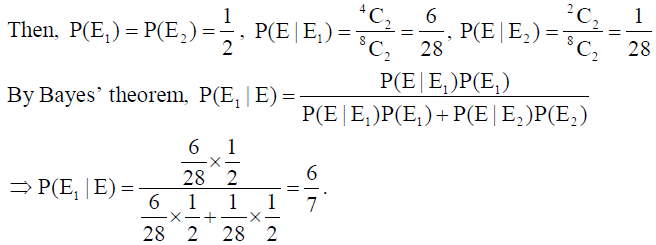
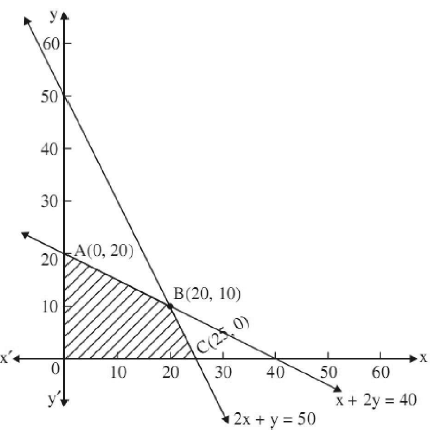
26. One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes. Formulate the above as an LPP and solve it graphically.
Solution: Let x be the number of cakes of one kind and y be the number of cakes of other kind.
To maximize: Z = (x + y)
Subject to constraints:
200x + 100y ≤ 5000 ⇒ 2x + y ≤ 50
25x + 50y ≤ 1000 ⇒ x + 2y ≤ 40; x, y ≥ 0

Clearly, maximum value of Z is 30.
Hence the no. of cake of one kind = 20,
and , the no. of cake of another kind = 10.