Class 12 Mathematics Sample Paper Term 1 Set B

Please refer to Class 12 Mathematics Sample Paper Term 1 Set B with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.

CBSE Class 12 Mathematics Sample Paper for Term 1

SECTION-A

In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.

1. What is the domain of the cos–1 x?
(A) [–∞, ∞]
(B) (–∞, ∞)
(C) (–1, 1)
(D) [–1, 1]

2. Find dy/dx where x = a cos² θ and y = b sin² θ .
(A) -b/a
(B) -b/a sec θ
(C) -b/a tanθ
(D) -b/a cot θ

3. Evaluate the determinant Δ=

(A) 0
(B) 27
(C) –27
(D) 5

4. If matrix A =[1 2 3]. Write A. A’ where A’ is the transpose of matrix A.
(A) 7
(B) 21
(C) 14
(D) 28

5. At what angle, the tangent to curve y = 3x² −x³ at x = 2 makes with positive x-axis?
(A) 45°
(B) 0°
(C) 30°
(D) 60°

6. For the given matrix , the values of y is

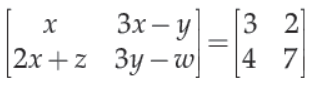
(A) x = 3
(B) x = 14
(C) y = 7
(D) y = –2

7. Set A has 3 elements and set B has 4 elements. Then the number of injective mappings that can be defined from A to B is
(A) 144
(B) 12
(C) 24
(D) 64

8. Find the minimum and maximum values of the given determinant Δ=

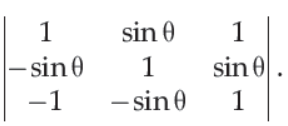
(A) 2 and 4
(B) –1 and 1
(C) 0 and 1
(D) –1 and 2

9. Which of the function is continuous in R?
(A) log x
(B) sin x
(C) 3x²
(D) All of these

10. If a relation R on the set {1, 2, 3} be defined by R = {(1, 1)}, then R is
(A) reflexive 
(B) transitive
(C) symmetric
(D) None of these

11. What is the principal value branch of tan -1 x ?
(A) -π/2 , π/2
(B) [–1, 1]
(C) (–∞, ∞)
(D) [-π/2 , π/2]

12. What is the derivative of xe x log ?
(A) xx (1+log x)
(B) log xe
(C) ex log x
(D) xe (1+log x)

13. Consider a square matrix A =

(A) Diagonal matrix
(B) Identity matrix
(C) Scalar matrix
(D) Null matrix

14. If y = x6 + logx² then the value of dy/dx is
(A) 6x⁵ – 2x
(B) 6x⁵ + 2/x
(C) 6x⁵ – 2/x
(D) 6x⁶ + x²

15. If A =

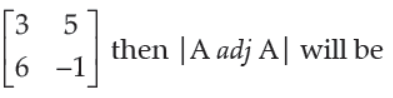
(A) 95
(B) 0
(C) 950
(D) 957

16. Two numbers x and y related to each other as x – y = 3. What is the value of the numbers such that their product is minimum?
(A) x = 2.5, y =−0.5
(B) x =1.5, y =−1.5
(C) x = 5.5, y = 2.5
(D) x =1, y =−2

17. The points on the curve x²/9 + y2/16 = 1 at which the tangent are parallel to y-axis.
(A) (±3, 0)
(B) (0, ±3)
(C) (±2, 0)
(D) (0, ±2)

18. The points on the curve x²/9 + y2/16 =1. at which the tangents are parallel to y-axis.
(A) (± 3, 0)
(B) (0, ± 3)
(B) (± 2, 0)
(B) (0, ± 2)

19. Objective functions
Maximise Z = 22x + 18y
Constraints : x + y ≤ 20
360x + 240y ≤ 5,760
Or 3x + 2y ≤ 48
x ≥ 0, y ≥ 0

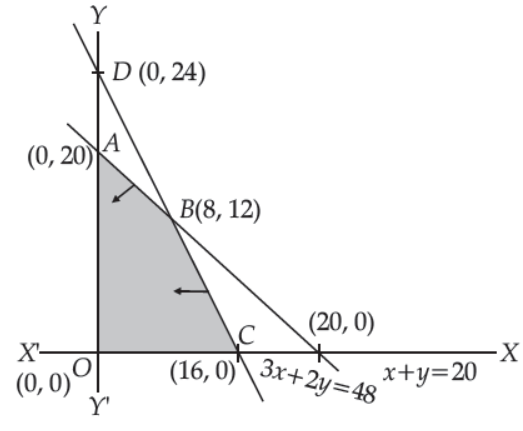
The maximum Z =
(A) 5,760
(B) 392
(C) 362
(D) 290

20. Which of the following is true for the function f(x) = In x + 2 increasing.
(A) function is strictly increasing in (1,2).
(B) function is strictly decreasing in (1,2).
(C) function is constant in (1,2).
(D) None of the above

SECTION-B

In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.

21. Let A = {a, b, c} and B = {1, 2, 3} and f: A ® B is defined by f = {(a, 2), (b, 1), (c, 3)}. Is the function oneone and onto.
(A) both one-one and onto
(B) only one-one
(C) only onto
(D) neither of them

22. Find the dy/dx of yx + xy = 0 ?

(C) 0
(D) None of these

23. Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function.
The minimum value of F occurs at
(A) (0, 2) only
(B) (3, 0) only
(C) the mid-point of the line segment joining the points (0, 2) and (3, 0) only
(D) any point on the line segment joining the points (0, 2) and (3, 0)

24. Consider the curve y = x²/4 . The Slope of the line parallel to tangent to the curve at x = 1 is
(A) 1/4
(B) 1/3
(C) -1/2
(D) 1/2

25. If

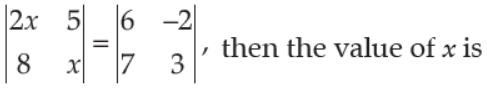
(A) 3
(B) ±3
(C) ±6
(D) 6

26. Given a function f (x)= 2x³ −21x² +60x+48 , it has local maximum at x =
(A) 2
(B) 3
(C) 5
(D) 4

27. The principal value of sin -1 (-1/√2) is :
(A) π/4
(B) π/6
(C) -π/4
(D) π/3

28. Suppose P and Q are two different matrices of order 3 × n and n × p, then the order of the matrix P × Q is ?
(A) 3 × p
(B) p × 3
(C) n × n
(D) 3 × 3

29. Let f(x) = |sin x|, then
(A) f is everywhere differentiable
(B) f is everywhere continuous but not differentiable at x = n π, n ∈ Z.
(C) f is everywhere continuous but not differentiable at x = (2n + 1) π/2 , n ∈ Z.
(D) none of these

30. If function f : R → R defined as f(x) = x² then f(x) is
(A) onto
(B) one-one and onto
(C) one-one
(D) None of these

31. Which of these intervals, the function f (x)= √2 cos x+x−35 is monotonic?
(A) (2π/3 , π)
(B) (0,π/3)
(C) (π/2 , π)
(D) (0,π/4)

32. If [x 1]

(A) 0
(B) –2
(C) –1
(D) 2

33. Objective function :
Maximise Z = 1000x + 600y
Constraints:
x + y ≥ 200
y ≥ 20, x ≥ 0
y ≥ 4x

Z is maximum at point
(A) (20, 80)
(B) (20, 180)
(C) (0, 0)
(D) (40, 160)

34. A particle moves along the curve x² = 2y. The point at which, ordinate increases at the same rate as the abscissa is ________
(A) (1, 2)
(B) (1/2 , 1)
(C) (1/2 , 1/2)
(D) (1,1/2)

35. If A = [2 –3 4], B =

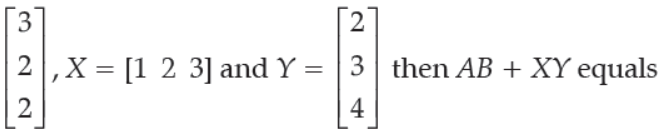
(A) [28]
(B) [24]
(C) 28
(D) 24

36. If function f(x) = 2x + 5/10x – 2 Then the domain of the function is :
(A) R−{1/2}
(B) R
(C) R – {1}
(D) R – {5}

37. The maximum number of equivalence relations on the set A = {1, 2, 3} are
(A) 1
(B) 2
(C) 3
(D) 5

38. If A is any square matrix of order 3 × 3 such that |A| = 3, then the value of |adj A| is?
(A) 3
(B) 1/ 3
(C) 9
(D) 27

39. The equation of tangent to the curve y(1 + x²) = 2 – x, where it crosses x-axis is :
(A) x + 5y = 2
(B) x – 5y = 2
(C) 5x – y = 2
(D) 5x + y = 2

40. A = [a_ij]m×n is a square matrix, if
(A) m < n
(B) m > n
(C) m = n
(D) None of these

SECTION-C

In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.

41. A dealer in rural area wishes to purchase a number of sewing machines. He has only `5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him `360 and a manually operated sewing machine `240. He can sell an electronic sewing machine at a profit of `22 and a manually operated machine at a profit of `18. Assume that the electronic sewing machines he can sell is x and that of manually operated machines is y.

The objective function is _______.
(A) Maximise Z = 360x + 240y
(B) Maximise Z = 22x + 18y
(C) Minimise Z = 360x + 240y
(D) Minimise Z = 22x + 18y

42. The maximum value of sin x. cos x is
(A) 1/4
(B) 1/2
(C) √2
(D) 2 √2

43. The maximum value of (1/x)x is :
(A) e
(B) e^e
(C) e1/e
(D) (1/e)^1/e

44. From the figure, which point is not belongs to feasible region

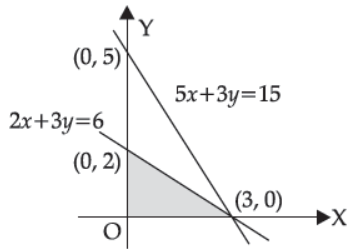
(A) (0, 2)
(B) (3, 0)
(C) (2, 3)
(D) (0, 0)

45. Which of the given values of x and y make the following pair of matrices equal

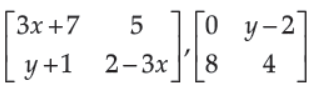
(A) x = -1/3 , y = 7
(B) Not possible to find
(C) y = 7 , x = -2/3
(D) x = -1/3 , y = -2/3

CASE-STUDY

The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – 1/2 x² where x is the number of days exposed to sunlight.

Based on the given information, answer the following questions.

46. The rate of growth of the plant with respect to sunlight is ______ .
(A) 4x –(1/2)x²
(B) 4 – x
(C) x – 4
(D) x –1/2 x²

47. What is the number of days it will take for the plant to grow to the maximum height?
(A) 4
(B) 6
(C) 7
(D) 10

48. What is the maximum height of the plant?
(A) 12 cm
(B) 10 cm
(C) 8 cm
(D) 6 cm

49. What will be the height of the plant after 2 days?
(A) 4 cm
(B) 6 cm
(C) 8 cm
(D) 10 cm

50. If the height of the plant is 7/2 cm, the number of days it has been exposed to the sunlight is _____ .
(A) 2
(B) 3
(C) 4
(D) 1