Class 12 Mathematics Sample Paper Set L

Please refer to Class 12 Mathematics Sample Paper Set L with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.

Question 1. Equation of straight line ax + by + c = 0 where 3a+4b+ c = 0, which is at maximum distance from (1, –2), is
(a) 3x + y – 17 = 0
(b) 4x + 3y – 24 = 0
(c) 3x + 4y – 25 = 0
(d) x + 3y – 15 = 0

Question 2.

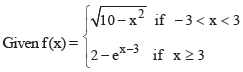
The graph of f(x) is –
(a) continuous and differentiable at x = 3
(b) continuous but not differentiable at x = 3
(c) differentiable but not continuous at x = 3
(d) neither differentiable nor continuous at x = 3

Question 3. The solution of the equation 2 = |z| + 2i, where z is a complex number, is –
(a) z = √3/3 − i
(b) z = √3/3 + i
(c) z = √3/3 ± i
(d) None of these

Question 4. The equation (5x – 1)² + (5y – 2)² = (λ² – 4λ + 4) (3x + 4y – 1)² represents an ellipse if λ ∈
(a) (0, 1]
(b) (–1, 2)
(c) (2, 3)
(d) (–1, 0)

Question 5. The straight line y = m (x – a) meets the parabola y² = 4ax in two distinct points for –
(a) all m ∈ R
(b) all m ∈ [–1, 1]
(c) all m ∈ R – {0}
(d) None of these

Question 6. p ∨ (p ∧ q) is equivalent to –
(a) q
(b) p
(c) ~p
(d) ~q

Question 7.

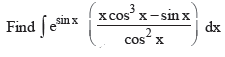
(a) x e^{sin x} – e^{sin x} sec x + C
(b) x e^{cos x} – e^{sin x} sec x + C
(c) x² e^{sin x} + e^{sin x} sec x + C
(d) 2x e^{sin x} – e^{sin x} tan x + C

Question 8. The function f : [2, ∞) → (0, ∞) defined by f (x) = x² – 4x + a, then the set of values of ‘a’ for which f(x) becomes onto is
(a) (4,∞)
(b) [4, ∞)
(c) {4}
(d) Φ

Question 9. If α and β are the real roots of the equation x² – (k – 2) x + (k² + 3k + 5) = 0 (k ∈ R). Find the maximum and minimum values of (α² + β²).
(a) 18, 50/9
(b) 18, 25/9
(c) 27, 50/9
(d) None of these

Question 10. The sum of the coefficient of all the terms in the expansion of (2x – y + z)²⁰ in which y do not appear at all while x appears in even powers and z appears in odd powers is –
(a) 0
(b) (2²⁰ – 1)/2
(c) 2¹⁹
(b) (3²⁰ – 1)/2

Question 11. All the five digit numbers in which each successive digit exceeds is predecessor are arranged in the increasing order. The (105)^th number does not contain the digit
(a) 1
(b) 2
(c) 6
(d) All of these

Question 12. Three people each flip two fair coins. The probability that exactly two of the people flipped one head and one tail, is–
(a) 1/2
(b) 3/8
(c) 5/8
(d) 3/4

Question 13. If a̅, b̅, c̅ are non-coplanar unit vector such that a̅ × (b̅ × c̅) = 1/2 (b̅ + c̅) then the angle between the vectors a̅, b̅ is
(a) 3π/4
(b) π/4
(c) π/8
(d) π/2

Question 14. The greatest and the least value of |z₁ + z₂| if z₁ = 24 + 7i and |z₂| = 6 respectively are
(a) 25, 19
(b) 19, 25
(c) –19, –25
(d) –25, –19

Question 15. Let P = (–1, 0), Q = (0, 0) and R = (3, 3√3 ) be three point. The equation of the bisector of the angle PQR is
(a) (√3/2)x + y = 0
(b) x + √(3y) = 0
(c) √3x + y = 0
(d) x + (√3/2)y = 0

Question 16. If ∫ √2 √(1+ sin x)dx = -4cos (ax + b) + C then the value of (a, b) is :
(a) 1/2, π/4
(b) 1,π/2
(c) 1, 1
(d) None of these

Question 17. Let f : R → R and f_n(x) = f (f_n–1 (x)) ∀ n ≥ 2, n ∈ N, the roots of equation f₃(x) f₂(x) f(x) – 25f₂(x) f(x) + 175 f(x) = 375. Which also satisfy equation f(x) = x will be
(a) 5
(b) 15
(c) 10
(d) Both (a) and (b)

Question 18. A triangle ABC satisfies the relation 2 sec 4C + sin² 2A + √(sinB) = 0 and a point P is taken on the longest side of the triangle such that it divides the side in the ratio 1 : 3. Let Q and R be the circumcentre and orthocentre of ΔABC. If PQ : QR : RP = 1 : α : β, then the value of α² + β².
(a) 9
(b) 8
(c) 6
(d) 7

Question 19.

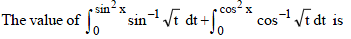
(a) π
(b) π/2
(c) π/4
(d) 1

Question 20. If a is real and √2ax + sinBy + cosBz = 0, x + cosBy + sinBz = 0 , – x + sin By – cos Bz = 0, then the set of all values of a for which the system of linear equations has a non-trivial solution, is –
(a) [1,2]
(b) [–1, 1]
(c) [1, ∞]
(d) [2^–1/2, 2^1/2]

Question 21. Box contains 2 one rupee, 2 five rupee, 2 ten rupee and 2 twenty rupee coin. Two coins are drawn at random simultaneously. The probability that their sum is Rs. 20 or more, is _________.

Question 22. The value of the definite integral,

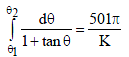
 where θ₂ = 1003π/2008 and θ₁ = π/2008. The value of K equals _________.

Question 23. The expansion of (1 + x)n has 3 consecutive terms with coefficients in the ratio 1 : 2 : 3 and can be written in the form ⁿC_k : ⁿC_k+1 : ⁿC_k+2. The sum of all possible values of (n + k) is _________.

Question 24. The mean and standard deviation of 6 observations are 8 and 4 respectively. If each observation is multiplied by 3, find the new standard deviation of the resulting observations.

Question 25.

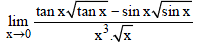
equals _________.