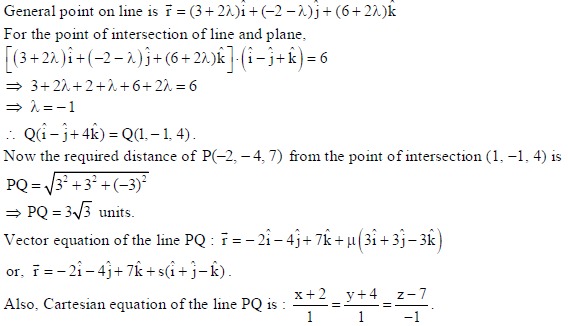Please refer to Class 12 Mathematics Sample Paper Set E with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
PART – A
Section I
Questions in this section carry 1 mark each.
1. Evaluate ∫ x sin xdx .
Answer: ∫ x sin xdx = x∫ sin xdx −∫(d/dx (x) ∫sin xdx)dx
= −x cos x + ∫1×cos x dx
= −x cos x + sin x +C.
OR
Evaluate ∫sin3 x cos xdx .
Answer: Put sin x = t ⇒ cos xdx = dt
∫sin3 x cos xdx = ∫ t3 dt
= 1/4 t4+ C
=1/4 sin4 x + C.
2. Check if the function f : N → N defined by f (x) = 2 − 3x is one-one or not?
Answer: Let f (x1) = f (x2) for x1, x2 x ∈ N .
⇒ 2 −3x1 = 2 − 3x2
⇒ x1 = x2
Clearly, f (x) is one-one.
3. Write the general solution of following differential equation :
dx/dy = 3y−x
Answer:
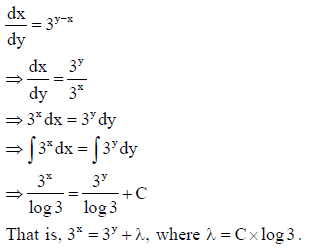
4. Find the direction cosines of a line which makes equal angles with the coordinate axes.
Answer: Given that α = β = γ , where α, β, γ are the direction angles made by the line with x, y, z-axes respectively.
As cos2 α + cos2 β + cos2 γ =1
⇒ 3cos2 α =1/3
⇒ cos2 α = 1/3
⇒ cos α = ± 1/√3
Therefore, the direction cosines of line are ± 1/√3 , ± 1/√3 ,± 1/√3
OR
Write the Cartesian equation of the line r̅ = 5î − 4ĵ+ 6k̂ + λ(3î + ĵ− 2k̂) .
Answer: Cartesian equation of line : x − 5/3 = y + 4/1 = z − 6/−2
5. If the relation R in the set {1, 2, 3} given by R = {(1,2),(2,1), (1,1)} . Then state if R is transitive relation, justify your answer.
Answer: As (2,1) and (1, 2) ∈ R but (2, 2)∉ R so, R can’t be transitive.
6. A bag contains 5 red and 3 blue balls. If 3 balls are drawn at random without replacement, then find the probability of getting exactly one red ball.
Answer: Required probability = P(RBB) + P(BRB) + P(BBR)
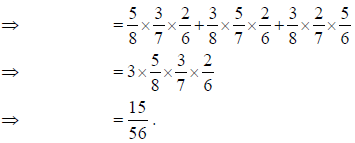
OR
If P(X) = 2/5 ,P(Y) = 3/10 , P(X ∩ Y) = 1/5 , then find the value of P(X’|Y’) .
Answer:
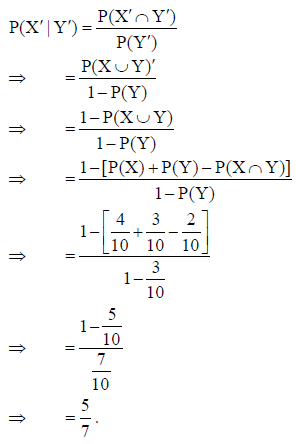
7. What is the acute angle between î − ĵ+ k̂ and − 2î + ĵ− k̂ ?
Answer: Let θ be the required angle between the vectors.
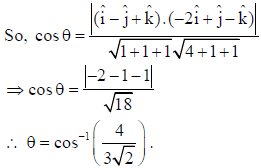
8. Simplify :
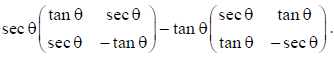
Answer:
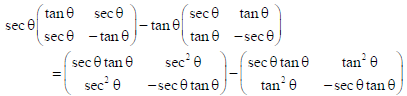
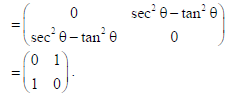
9. If A is an order 3 matrix, and A’A = I then, find the value of |2(adj.A)−1| .
Answer:
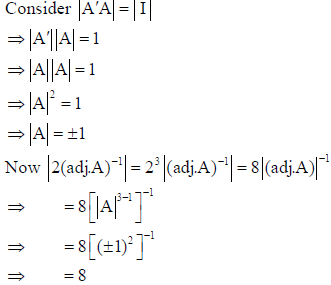
OR
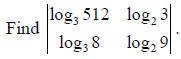
Answer:
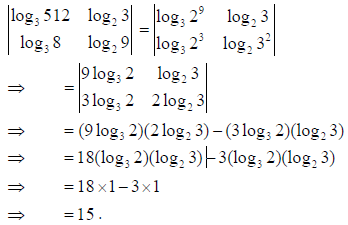
10. Let a̅ = î + 2ĵ+ k̂ and b̅ = î − ĵ denote the sides of a triangle, find the area of this triangle.
Answer:
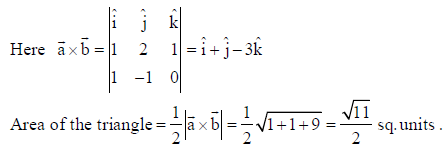
11. If E and F are events such that 0 < P(F) <1, then write the value of P(E | F) + P(E’|F) .
Answer:
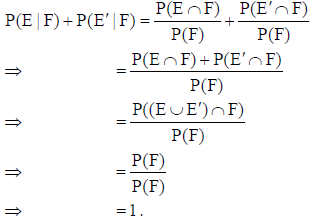
12. Find the vector equation of a line passing through the point (– 1, 5, 4) and perpendicular to the plane z = 0 .
Answer: The normal to the plane z = 0 is k̂
Clearly the required line through (–1, 5, 4) will be parallel to k̂ .
Hence the equation of line is given by
r̅ = – î + 5 ĵ+ 4k̂ + λ (k̂ ) .
OR
The z-coordinate of a point on the line joining A(5, 1, –2) and B(2, 2, 1) is ‘–1’. Find its xcoordinate.
Answer:
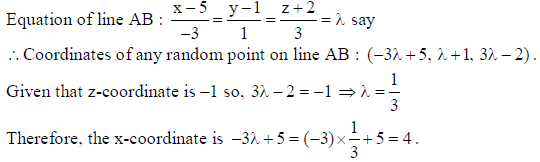
13. If a matrix has 18 elements, then how many possible orders it can have?
Answer: Possible orders are 1×18, 2×9, 3×6, 6×3, 9× 2, 18×1 i.e., 6.
14. Let a relation R in a set A contains (a1 , a2 ) ∈ R . If R is a symmetric relation, then write the element which must be in R.
Answer: R must contain (a2 , a1 )∈R
15. If the projection of a̅ = î – 2ĵ+ 3k̂ on b̅ = 2î + λk̂ is zero, then find the value of λ .
Answer:
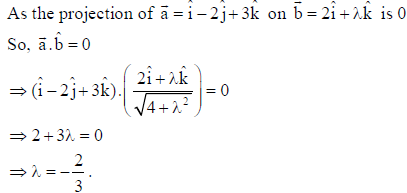
16.
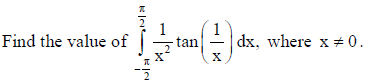
Answer:
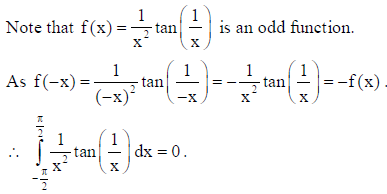
Section II
Questions in this section carry 1 mark each.
Both the Case study based questions are compulsory. Attempt any 4 sub-parts from each question
17 (i-v) and 18 (i-v).
17. In a city school, all class XII students have Mathematics and Biology as their main subjects,
apart from three other subjects which include one language.
The school conducted pre-board examination for class XII. In the examination, it is observed that 30% of the students failed in Biology, 25% failed in Mathematics and 12% failed in both Biology and Mathematics . A student is selected at random from the school.

Using the information given above, answer the following :
(i) The probability that the selected student has failed in Biology, if it is known that he has failed in Mathematics, is
(a) 30%
(b) 25%
(c) 48%
(d) 12%
Answer
C
(ii) The probability that the selected student has failed in Mathematics, if it is known that he
has failed in Biology, is
(a) 48%
(b) 40%
(c) 88%
(d) 12%
Answer
B
(iii) The probability that the selected student has failed in at least one of the two subjects, is
(a) 88%
(b) 40%
(c) 43%
(d) 60%
Answer
C
(iv) The probability that the selected student has passed in at least one of the two subjects, is
(a) 25%
(b) 88%
(c) 22%
(d) 43%
Answer
B
(v) The probability that the selected student has passed in Mathematics, if it is known that he has failed in Biology, is
(a) 1/5
(b) 2/5
(c) 3/5
(d) 4/5
Answer
C
18. An online retail company ships its products in the cartons.
Each of the cartons is made by a rectangular sheet of fiberboard with dimensions of 8 m by 3 m.
While making the carton, equal squares of side length ‘x’ metres are cut-off from each corner of the rectangular sheet of fiberboard. After that, the resulting flaps are folded up to form the carton.
See the figure given below to identify the sides of the carton.
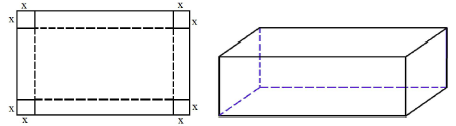
Based on the above information, answer the following :
(i) The volume V of the carton is given by V = f (x) , then f (x) equals
(a) 22x − 24x2 + 4x3
(b) 1/24 − 1/22 + 1/4x3
(c) 24x + 22x2 − 4x3
(d) 24x − 22x2 + 4x3
Answer
D
(ii) Consider the function f (x) obtained in (i). Then f ‘(x) equals
(a) 24+ 44x −12x2
(b) 24− 44x +12x2
(c) 8x − 22
(d) 22− 48x +12x2
Answer
B
(iii) The value of x (in metres) for which the volume V of the carton is maximum, is
(a) 3
(b) 2/3
(c) both (a) and (b)
(d) none of (a) and (b)
Answer
B
(iv) What is the length (in metres) of the carton formed, for maximum value of V?
(a) 1/3
(b) 5/3
(c) 20/3
(d) 2/3
Answer
C
(v) What is the maximum volume of the carton formed?
(a) 200/7 m3
(b) 81 m3
(c) 200/27 m3
(d) 200/27 m3
Answer
D
PART – B
Section III
Questions in this section carry 2 marks each.
19. If x = at2 , y = 2at, then find d2y/dx2 at t = 1/2.
Answer:

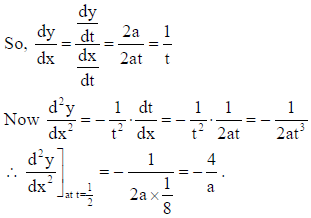
20. Find
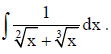
Answer:
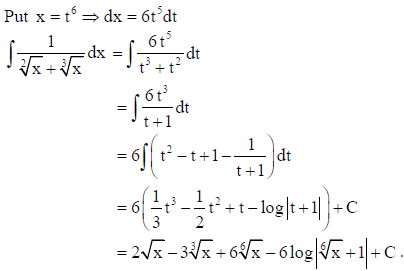
OR
Evaluate
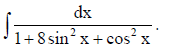
Answer:
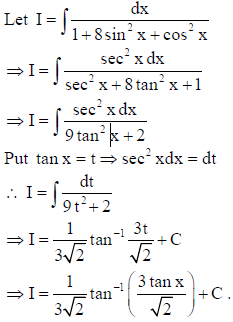
21. A wallet contains 3 silver and 6 copper coins and a second wallet contains 4 silver and 3 copper coins. If a coin is drawn at random from one of the two wallets, find the probability that it is a silver coin.
Answer: Let E1 : coin is drawn from the first wallet and E2 : coin is drawn from the second wallet.
Also let A : silver coin is drawn.
22. Simplify :
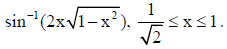
Answer: Put x = cosθ ⇒ θ = cos−1 x
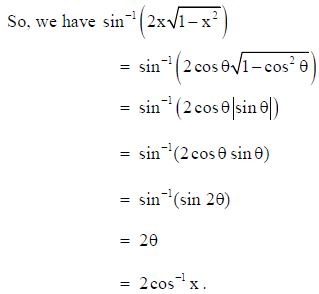
23. Let A be a square matrix of order ‘k’ such that
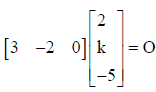
where O is the null matrix and det.(A) is 7. Then, write the value of det.(2 adj.A).
Answer:
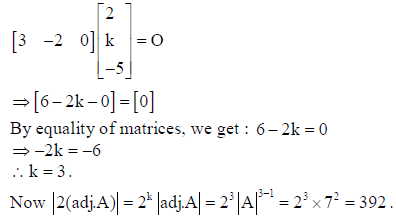
OR
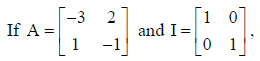
find scalar k so that A2 + I = kA .
Answer:
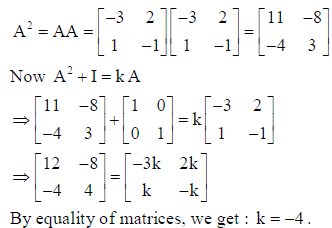
24. Solve :
Answer:
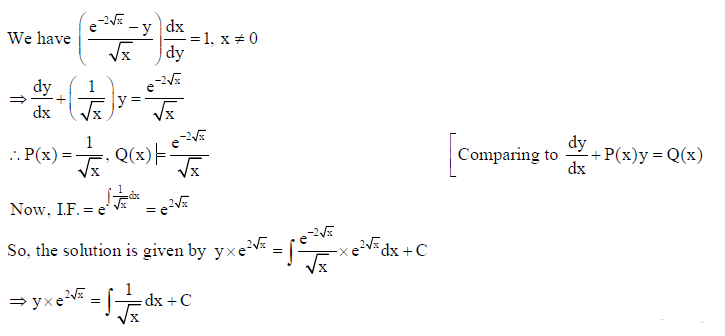
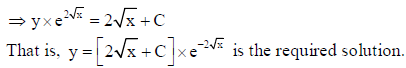
25. Find the distance between the planes r̅ .(2î − 4ĵ+ 2k̂ ) = 3 and r̅ .(î − 2ĵ+ k̂ ) + 5 = 0 .
Answer:
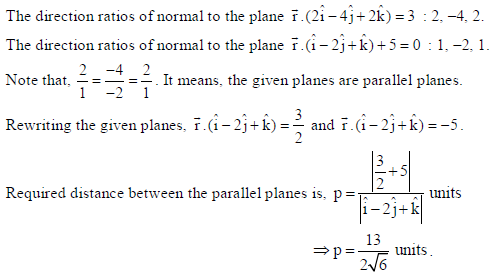
26. Find the points on the curve y = x3 – 3x2 – 4x at which the tangent lines are parallel to the line
8x + 2y – 3 = 0 .
Answer: For y = x3 – 3x2 – 4x , we have
dy/dx = 3x2 – 6x – 4
Slope of tangent is ‘–4’ as tangent lines are parallel to 8x + 2y – 3 = 0 , whose slope is ‘–4’.
Note that the parallel lines have same slope.
That is, 3x2 – 6x – 4 = –4
⇒ 3x(x – 2) = 0
∴ x = 0 ; x = 2
Therefore, the required points on the curve are (0, 0); (2, – 12) .
27. Find the area bounded by y2 = x, y = 5 , and y-axis.
Answer: We have y2 = x, y = 5 , x = 0
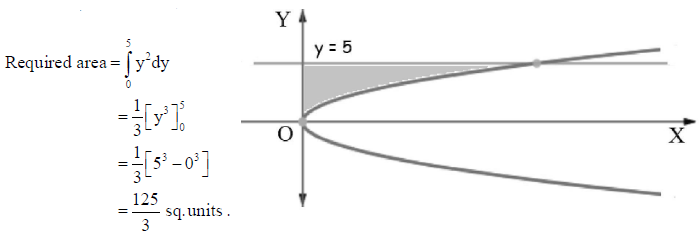
28. Find all the unit vectors perpendicular to the plane PQR, where P(3, –1, 2), Q(1, –1, –3) and R(4, –3, 1).
Answer:
OR
Given that|a̅|=1 and |b̅|=1. Find the angle between the vectors a̅ and b̅ , so that √3a̅ + b̅ is a
unit vector.
Answer:
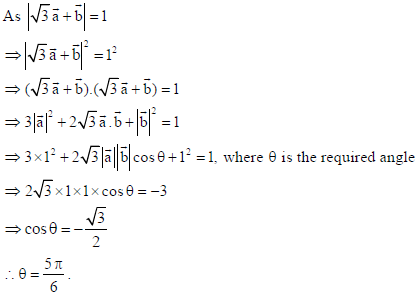
Section IV
Questions in this section carry 3 marks each.
29. Find the intervals in which the function f (x) = (x −1)3 (x − 2)2 is
(a) strictly increasing
(b) strictly decreasing.
Answer:

30. If y = ex²cos x + (cos x)x , then find dy/dx.
Answer:
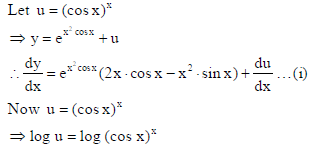
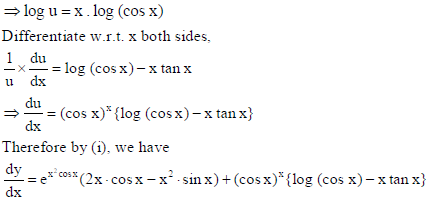
OR
Find d2y/dx2 at t = π/3, if y = 3cos t − cos3t and x = 3sin t −sin 3t.
Answer:
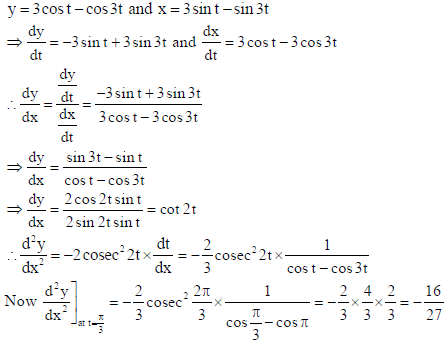
31. Find the area bounded by the lines y = || x | −1| and the x-axis. Use integration.
Answer:
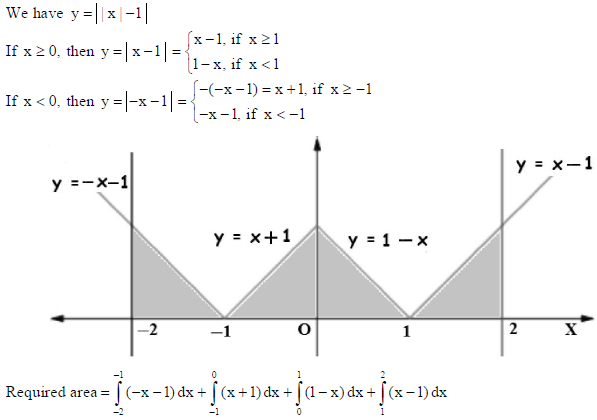
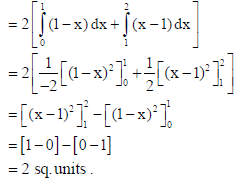
32. Let N be the set of natural numbers and R be the relation on N × N defined by (a, b) R (c, d) iff ad = bc for all a, b, c, d∈N. Show that R is an equivalence relation.
Answer:
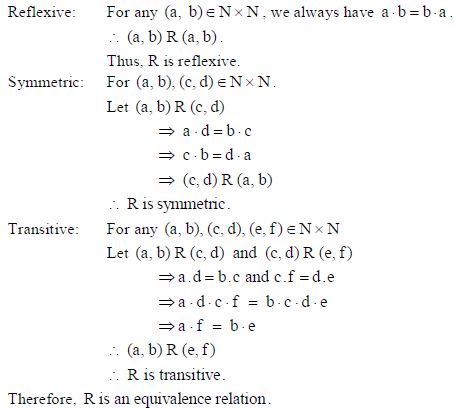
33. Evaluate
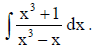
Answer:

OR
Evaluate
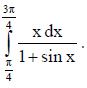
Answer:
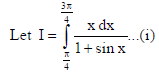
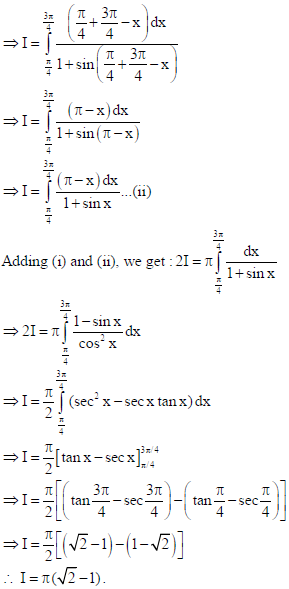
34.
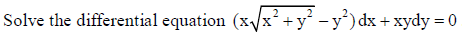
Answer:
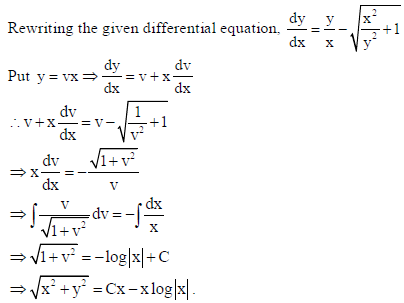
35.
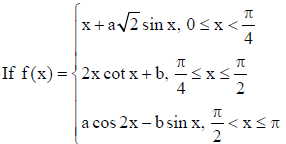
is continuous in x∈[0,π] , then find the value of a and b.
Answer: As f (x) is continuous in x∈[0,π] so, it will be continuous at x = π/4 and x = π/2.
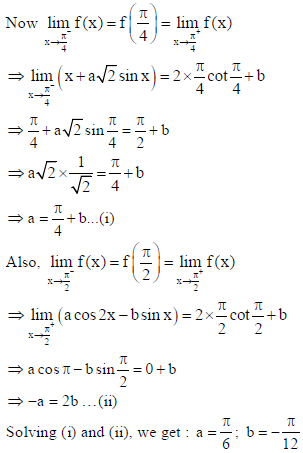
Section V
Questions in this section carry 5 marks each.
36.
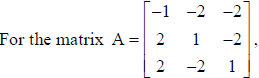
find the value of det. A and adj.A. Hence, show that 3 A(adj.A) = |A| I3 = (adj.A)A .
Answer:

Hence, A(adj.A) = A I3= (adj.A)A .
OR
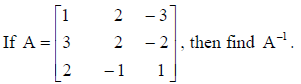
Using the inverse of matrix A, solve the following system of equations :
x + 2y – 3z = 6, 3x + 2y – 2z = 3, 2x – y + z = 2.
Answer:
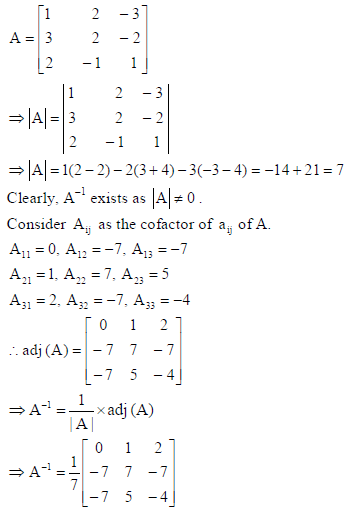

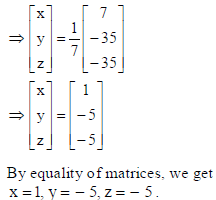
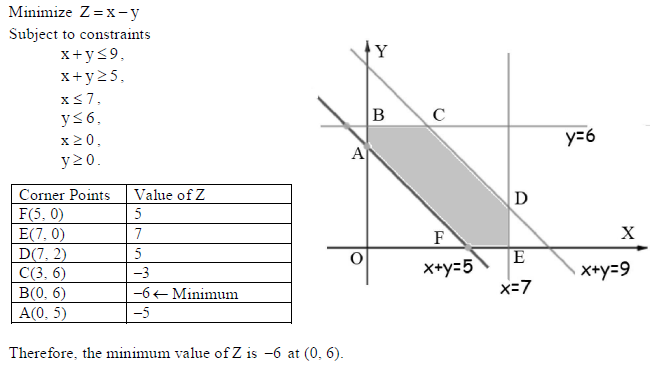
37. Solve the following linear programming graphically :
Minimize Z = x − y
Subject to constraints
x + y ≤ 9 ,
x + y ≥ 5 ,
x ≤ 7 ,
y ≤ 6 ,
x ≥ 0 ,
y ≥ 0 .
At what point, the minimum value of Z occurs?
Answer:
OR
Using graphical method, solve the following linear programming :
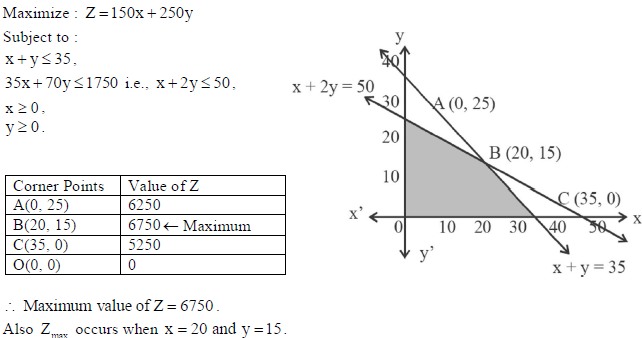
Maximize : Z =150x + 250y
Subject to :
x + y ≤ 35 ,
35x + 70y ≤1750 ,
x ≥ 0 ,
y ≥ 0 .
Also, write the x and y coordinate of the point at which Zmax occurs.
Answer:
38. Find the vector and Cartesian equations of the line which is perpendicular to the lines with equations
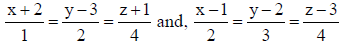
and passes through the point (1, 1, 1). Hence, write the direction cosines of the line thus obtained.
Answer: Let the d.r.’s of the required line L (say) be a, b, c.
So, a vector parallel to it will be b̅ = aî + bĵ+ ck̂

OR
Find the distance of the point P(–2, – 4, 7) from the point of intersection Q of the line r̅ = (3î – 2ĵ+ 6k̂ ) + λ(2î – ĵ+ 2k̂) and the plane r̅ .(î – ĵ+ k̂ ) = 6 . Also write the vector and Cartesian equation of the line PQ.
Answer: General point on line is r̅ = (3+ 2λ)î + (–2 – λ)ĵ + (6 + 2λ)k̂
For the point of intersection of line and plane,