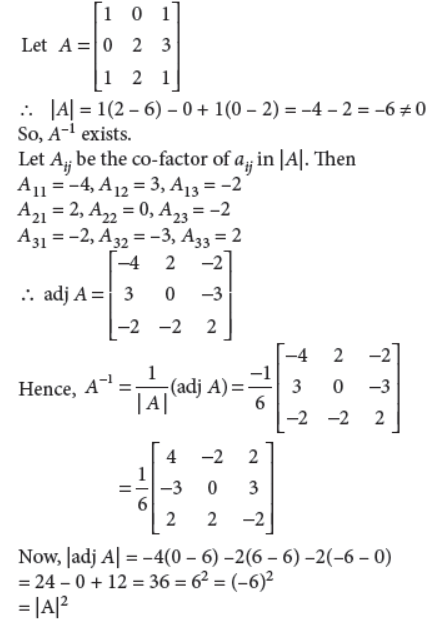Please refer to Class 12 Mathematics Sample Paper Set A with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
PART – A
Section – I
1. Evaluate :
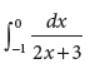
Answer :
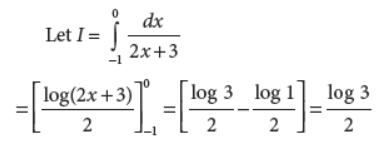
OR
Evaluate :
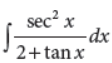
Answer :

2. Let A = {1, 2, 3, 4} and R be a relation in A given by R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1), (3, 1)}. Then, show that R is reflexive.
Answer : Here, A = {1, 2, 3, 4} and R = {(1, 1), (2, 2), (3, 3),
(4, 4), (1, 2), (2, 1), (3, 1)}
Now, (1, 1), (2, 2), (3, 3), (4, 4) ∈R;
∴ R is reflexive.
3. Show that the matrix
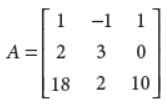
is not invertible.
Answer :
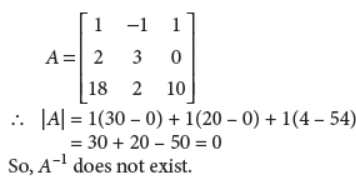
OR
Find the value of the determinant
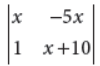
Answer :
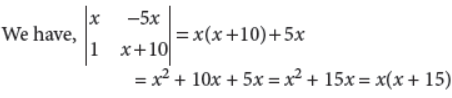
4. Find the equation of a plane with intercepts 2, 3 and 4 on the X, Y and Z-axes respectively.
Answer : As the plane has intercepts 2, 3 and 4 on X, Y and Z axes respectively.
∴ The required equation of the plane is
x/2 + y/3 + z/4 = 1
⇒ 6x + 4y + 3z = 12
5. Find the degree of the differential equation
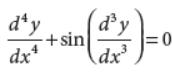
Answer : Since, the given differential equation cannot be expressed as a polynomial. So, its degree is not defined.
OR
Find the order of the differential equation
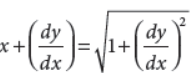
Answer :

6. Let A = {1, 2, 3} and B = {1, 2, 4}. Check whether f = {(1,1), (1,2), (2,1), (3, 4)} from A to B is a function or not.
Answer : Here, f is not a function from A to B as f (1) is not unique.
7. Let E and F be events associated with the sample space S of an experiment. Show that P(S|F) = P(F|F) = 1.
Answer : We know that,
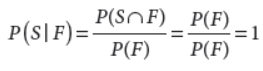
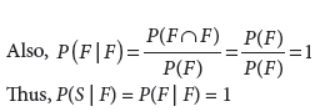
OR
Let A and B be two events associated with an experiment such that P(A ∩ B) = P(A)P(B). Show that P(A|B) = P(A) and P(B|A) = P(B).
Answer : Since, P(A ∩ B) = P(A)P(B), therefore, A and B are independent events.
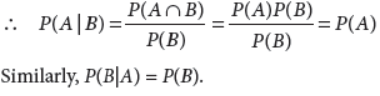
8. If
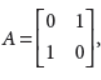
then find the value of A2.
Answer :
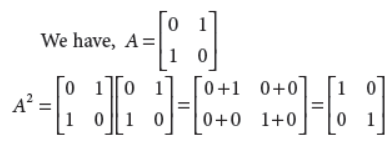
9. Find the angle between two vectors a̅ and b̅ with magnitude 1 and 2 respectively, such that a̅.b̅ = 1 .
Answer : We are given |a̅| = 1 |b̅| = 2 and a̅.b̅ = 1
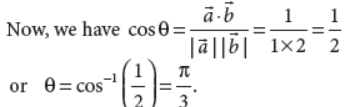
OR
Find the projection of, a̅ = 2î – ĵ + k̂ on b̅ = î – 2ĵ + k̂
Answer :
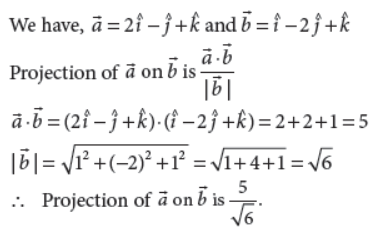
10. If P(A) = 3/8 , P(B) = 5/8 and P(A ∪ B) = 3/4 then find P(A | B) .
Answer : P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
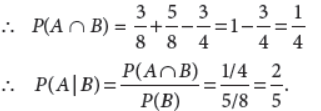
11. Suppose you have two coins which appear identical in your pocket. You know that, one is fair and one is 2 headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin?
Answer : Let E1 be the event that fair coin is drawn, E2 be the event that 2 headed coin is drawn, and E be the event that tossed coin get a head.
∴ P(E1) = 1/2, P(E2) = 1/2, P(E|E1) = 1/2 and P(E|E2) = 1
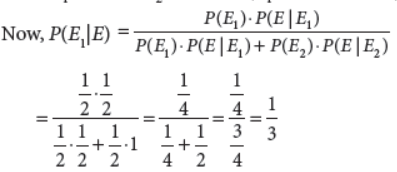
12. Show that f(x) = x2 + 1 is not one-one?
Answer : Since f(x) = f(–x) = x2 + 1 for all x ∈R, therefore, f is not one-one.
13. Suppose that five good fuses and two defective ones have been mixed up. To find the defective fuses, we test them one-by-one, at random and without replacement. What is the probability that we are lucky and find both of the defective fuses in the first two tests?
Answer : Let D1, D2 be the events that we find a defective fuse in the first, second test respectively.
Required probability = P(D1 ∩ D2)
= P(D1)P(D2 |D1 ) = 2/7.1/6 = 1/21
14. Evaluate :

Answer :
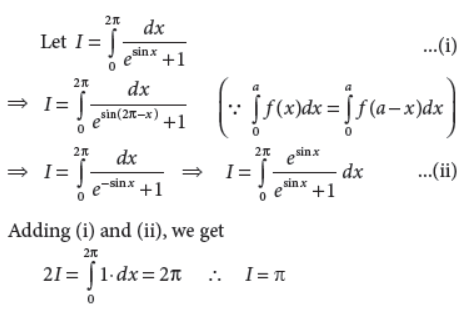
15. What is the distance between the planes 2x + 2y – z + 2 = 0 and 4x + 4y – 2z + 5 = 0 ?
Answer : Given planes are 2x + 2y – z + 2 = 0 and 4x + 4y – 2z + 5 = 0
Let point P(x1, y1, z1) lie on plane 2x + 2y – z + 2 = 0
⇒ 2x1 + 2y1 – z1 = –2
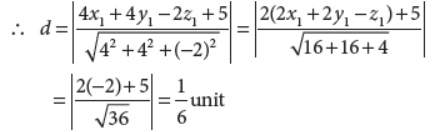
16. For matrix

Answer :
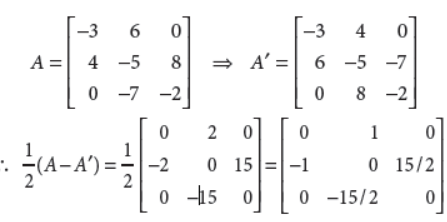
Section – II
Case study-based questions are compulsory. Attempt any 4 sub parts from each question. Each sub-part carries 1 mark.
17. If two vectors are represented by the two sides of a triangle taken in order, then their sum is represented by the third side of the triangle taken in opposite order.
(i) If p̅, q̅, r̅ are the vectors represented by the sides of a triangle taken in orders, then p̅+q̅ =
(a) r̅
(b) 2r̅
(c) –r̅
(d) None of these
Answer : C
(ii) If ABCD is a parallelogram and AC and BD are its diagonals, then A̅C̅ + B̅D̅ =
(a) 2D̅A̅
(b) 2A̅B̅
(c) 2B̅C̅
(d) 2B̅D̅
Answer : C
(iii) If ABCD is a parallelogram, where A̅B̅ = x̅ and B̅C̅ = y̅ then A̅C̅–B̅D̅ =
(a) x̅
(b) 2x̅
(c) y̅
(d) 2y̅
Answer : B
(iv) If ABCD is a quadrilateral whose diagonals are A̅C̅ and B̅D̅ , then B̅A̅ + C̅D̅ =
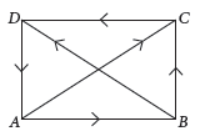
(a) A̅C̅ + D̅B̅
(b) A̅C̅ + B̅D̅
(c) B̅C̅ + A̅D̅
(d) B̅D̅ + C̅A̅
Answer : D
(v) If S is the mid point of side QR of DPQR, then P̅Q̅ + P̅R̅ =
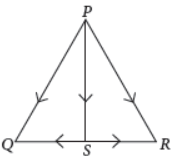
(a) 2O̅S̅
(b) 2P̅S̅
(c) 2S̅R̅
(d) None of these
Answer : B
18. A can manufacturer designs a cylindrical can for a company making sanitizer and disinfector.
The can is made to hold 5 litres of sanitizer or disinfector.
(i) If r cm be the radius and h cm be the height of the cylindrical can, then the surface area expressed as a function of r as

(a) 2πr2
(b) 2πr2 + 5000
(c) 2πr2 + 5000/r
(d) 2πr2 + 10000/r
Answer : D
(ii) The radius that will minimize the cost of the material to manufacture the can is
(a) 3√500/π cm.
(b) √500/π cm.
(c) 3√2500/π cm.
(d) √2500/π cm.
Answer : C
(iii) The height that will minimize the cost of the material to manufacture the can is
(a) 3√500/π cm.
(b) 23√2500/π cm.
(c) √2500/π cm.
(d) 2√2500/π cm.
Answer : B
(iv) If the cost of material used to manufacture the can is ₹ 100/m2 and 3√2500/π = 9 cm. then minimum cost is approximately
(a) ₹ 16.7
(b) ₹ 18
(c) ₹ 19
(d) ₹ 20
Answer : A
(v) To minimize the cost of the material used to manufacture the can, we need to minimize the
(a) volume
(b) curved surface area
(c) total surface area
(d) surface area of the base
Answer : C
PART – B
Section – III
19. Separate the interval [0,π/2] into sub-intervals in which the function f(x) = sin4x + cos4x is increasing or decreasing.
Answer : Here f(x) = sin4x + cos4x …(i)
On differentiating (i) w.r.t. x, we get
f ′(x) = 4sin3x cos x – 4 cos3x sin x = 4 sinx cosx (sin2x – cos2x) = –2 sin2x cos2x = –sin4x
Put f ′(x) = 0 ⇒ x = π/4

20. If a discrete random variable X has the following probability distribution :
| X = x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P (X = x) | k | 2k | 2k | 3k | k2 | 2k2 | 7k2+k |
Find the value of k.
Answer : k + 2k + 2k + 3k + k2 + 2k2 + 7k2 + k = 1
⇒ 10k2 + 9k – 1 = 0 ⇒ (10k – 1)(k + 1) = 0
⇒ k = 1/10 or K= –1
Since probability cannot be negative.
∴ k = 1/10
OR
An urn contains 10 black balls and 5 white balls. Two balls are drawn from the urn one after the other without replacement. Find the probability that both drawn balls are black.
Answer : Let E and F respectively denote the events that first and second ball drawn is black. We have to find P(E ∩ F) or P(EF).
Now, P(E) = P(black ball in first draw) = 10/15
and P(F | E) = 9/14
By multiplication rule of probability, we have
P(E ∩ F) = P(E) ⋅ P(F|E) = 10/15 X 9/14 = 3/7
21. Evaluate :
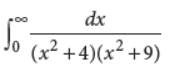
Answer :

22. Solve for x : cos(tan-1) sin(cot-1 3/4)
Answer :
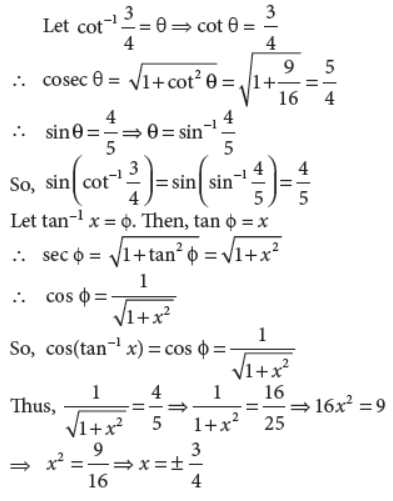
23. Evaluate : ∫(exloga + ealogx + ealoga)dx
Answer :

OR
Evaluate :
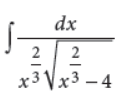
Answer :
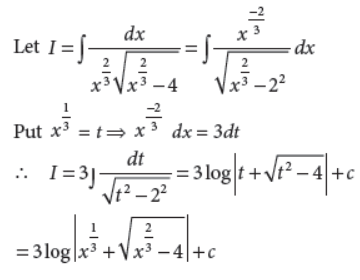
24. Find the solution of the differential equation dy/dx = cos (x+y)
Answer :

25. If
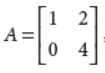
Answer :
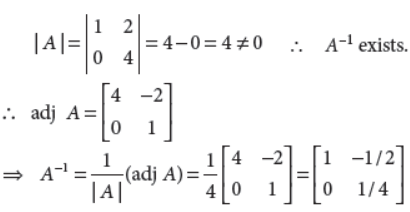
26. A box contains N coins, of which m are fair and the rest are biased. The probability of getting head when a fair coin is tossed is 1/2 , while it is 2/3 when a biased coin is tossed. A coin is drawn from the box at random and is tossed twice. The first time it shows head and the second time it shows tail. Find the probability that the coin drawn is fair.
Answer : Let E be the event that the coin tossed twice shows first head and then tail and F be the event that the coin drawn is fair.
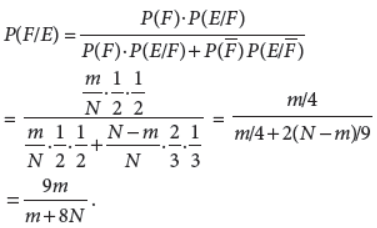
27. Find the values of a and b such that the function f defined by
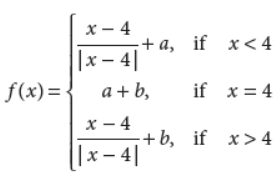
Answer :
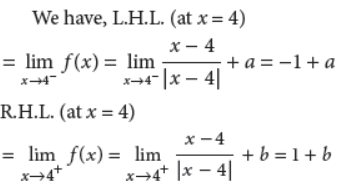
and f(4) = a + b
Since f(x) is continuous at x = 4.
∴ –1 + a = a + b ⇒ b = –1
and 1 + b = a + b ⇒ a = 1
Thus, f(x) is continuous at x = 4 if a = 1 and b = –1.
28. Find the cartesian equation of the plane passing through a point having position vector 2î+3ĵ+4k̂ and perpendicular to the vector 2î+ĵ-2k̂.
Answer : Here, (x1, y1, z1) = (2, 3, 4), a = 2, b = 1, c = –2
Cartesian equation is
a(x – x1) + b(y – y1) + c(z – z1) = 0
⇒ 2(x – 2) + 1(y – 3) –2(z – 4) = 0
⇒ 2x – 4 + y – 3 – 2z + 8 = 0
⇒ 2x + y – 2z = –1
OR
Find the distance of the point (–1, –5, –10) from the point of intersection of the line r̅ = 2î–ĵ+2k̂+λ(3î+4ĵ+12k̂) and the plane r̅ = (î–ĵ+2) =5.
Answer : Any point on line
r̅ = 2î–ĵ+2k̂+λ(3î+4ĵ+12k̂) IS (2+3λ, –1+4λ , 2+12λ
If it lies on the planer̅ = (î–ĵ+k̂)
then, 1(2 + 3λ) – 1(–1 + 4λ) + 1(2 + 12l) = 5
⇒ 2 + 3λ + 1 – 4λ + 2 + 12λ = 5
⇒ 11λ = 0 ⇒ l = 0
Putting l = 0 in (i), we get (2, –1, 2)
29. Let N be the set of all natural numbers and let R be a relation in N × N defined by (a, b) R(c, d) ⇒ ad = bc for all (a, b), (c, d) ∈ N × N, show that R is an equivalence relation on N × N.
Answer : Given (a, b) R(c, d)
⇒ ad = bc ∀ (a, b), (c, d) ∈ N × N
Reflexive : Let (a, b) ∈ N × N when a ∈ N, b ∈ N
(a, b) R (a, b) ⇒ ab = ba, which is true
So, R is reflexive.
Symmetric : Let (a, b), (c, d) ∈ N × N
(a, b) R (c, d) ⇒ ad = bc
⇒ cb = da ⇒ (c, d) R(a, b)
So R is symmetric.
Transitive : Let (a, b), (c, d), (e, f ) ∈ N × N
(a, b) R(c, d) ⇒ ad = bc
(c, d) R (e, f) ⇒ cf = de
⇒ adcf = bcde ⇒ af = be ⇒ (a, b) R (e, f )
So R is transitive.
Since R is reflexive, symmetric and transitive, so R is
an equivalence relation.
30. Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube.
Answer : Let V be the volume of a closed cuboid with length x, breadth x and height y. Let S be the surface area of cuboid. Then
x2y = V and S = 2(x2 + xy + xy) = 2(x2 + 2xy)
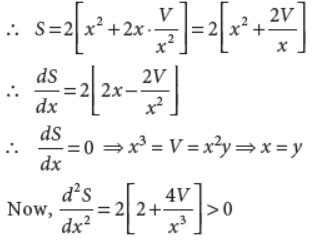
∴ x = y will give minimum surface area and
x = y, means all the sides are equal.
∴ Cube will have minimum surface area.
31. Solve : (x+y)2 dy/dx = a2
Answer :
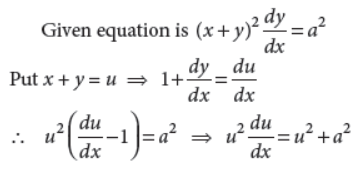
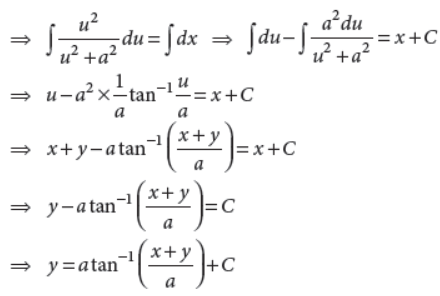
OR
Find one-parameter family of solution curve of the differential equation dy/dx cos2x = tanx – y.
Answer :
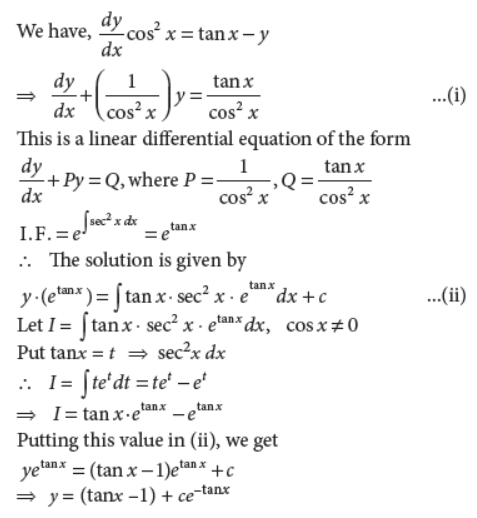
32. If x2/a2–y2/b2 = 1 , then prove that d2y/dx2 = –b4/a2y3.
Answer :
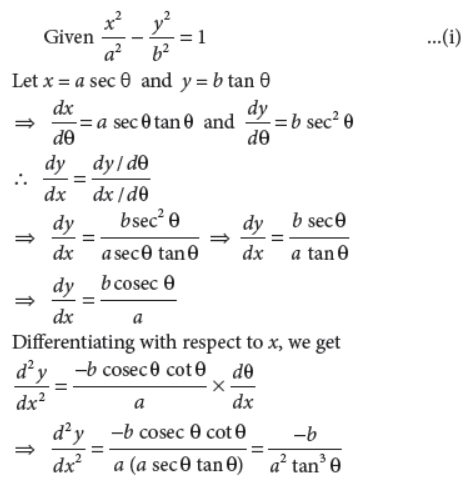
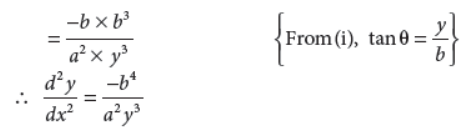
33. Evaluate :

Answer :
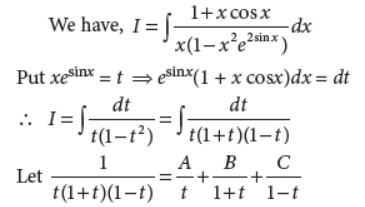
⇒ 1 = A(1 – t2) + B(t – t2) + C(t + t2)
Equating the coefficients of t2, t and constant terms,
we get A + B – C = 0, B + C = 0 and A = 1
Solving these equations, we get

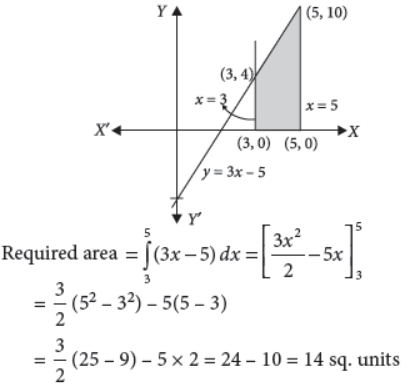
34. Find the area enclosed by y = 3x – 5, y = 0, x = 3 and x = 5.
Answer : We have, y = 3x –5, y = 0, x = 3, x = 5
OR
Using integration, find the area of the region bounded by the lines y – 1 = x, the X-axis and the ordinates x = –2 and x = 3.
Answer : The line y – 1 = x meets the X-axis at the point where y = 0, i.e., where 0 – 1 = x, i.e., at the point (–1, 0).
It meets Y-axis at the point where x = 0, i.e., where y – 1 = 0, i.e., at the point (0, 1).
Required area (shown shaded) is given by
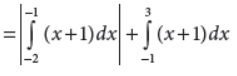
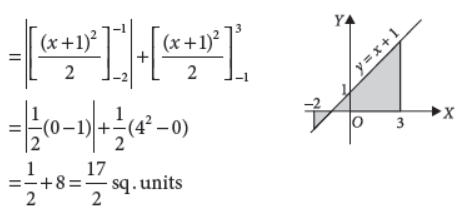
35. If x = 1–t2/1+t2 and 2t/1+t2 ,then find dy/dx.
Answer :
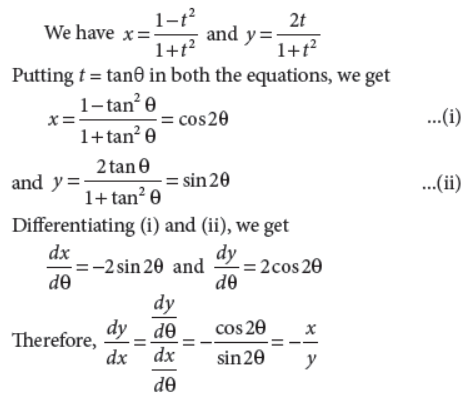
Section – V
36. The points A(4, 5, 10), B(2, 3, 4) and C(1, 2, –1) are three vertices of a parallelogram ABCD. Find the vector and cartesian equations of the sides AB and BC and find coordinates of D.
Answer : In a parallelogram, diagonals bisect each other.
∴ Mid point of BD = Mid point of AC

and vector equation of side BC is
r̅ = 2î+3ĵ+4k̂+λ(î+ĵ+5k̂)
OR
If the planes x – cy – bz = 0, cx – y + az = 0 and bx + ay – z = 0 pass through a straight line, then find the value of a2 + b2 + c2 + 2abc.
Answer :
Given planes are
x – cy – bz = 0 …(i)
cx – y + az = 0 …(ii)
bx + ay – z = 0 …(iii)
The d.r. ,s of normal to plane (i), (ii) and (iii) are (1, –c, –b), (c, –1, a) and (b, a, –1) respectively.
All planes pass through same line, then the line is perpendicular to each of the three normals.
The d.r’s. of line from planes (i) and (ii) are

⇒ ac2 + bc + a2bc + ab2 = a + bc – a3 – a2bc
⇒ c2 + abc + b2 = 1 – a2 – abc
⇒ a2 + b2 + c2 + 2abc = 1
37. Find the maximum value of Z = x + y subject to x + y ≤ 10, 3x – 2y ≤ 15, x ≤ 6, x ≥ 0, y ≥ 0.
Answer : Converting inequations into equations and drawing the corresponding lines, we have
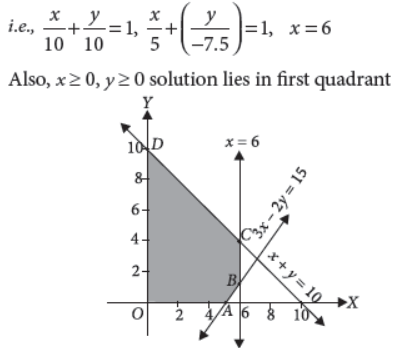
B is the point of intersection of the lines x = 6 and 3x – 2y = 15 i.e., B = (6 , 3/2)
C is the point of intersection of the lines x = 6 and x + y = 10 i.e., C ≡ (6, 4).
We have points A(5, 0), B (6,3/2) C(6, 4) and D(0, 10).
Now Z = x + y
∴ Z(O) = 0 + 0 = 0
Z(A) = 5 + 0 = 5
Z(B) = 6 +3/2 + = 7.5
Z(C) = 6 + 4 = 10
Z(D) = 0 + 10 = 10
∴ Z has maximum value 10 at two points C(6, 4) and D(0, 10).
OR
Find the maximum and minimum values of Z = 7x1 – 3x2 subject to x1 + 2x2 ≤ 2, 2x1 + 4x2 ≤ 8, x1 ≥ 0, x2 ≥ 0.
Answer : Converting inequations into equations and drawing the corresponding lines, we have

Also, x1 ≥ 0, x2 ≥ 0 solution lies in first quadrant.
We have points A(2, 0) and B(0, 1).
Now, Z = 7×1 – 3×2
∴ Z(O) = 7(0) – 3(0) = 0
Z(A) = 7(2) – 3(0) = 14
Z(B) = 7(0) – 3(1) = –3
∴ Z has maximum value 14 at point (2, 0) and minimum value –3 at point (0, 1).
38. Find a matrix X such that,
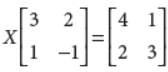
Answer :
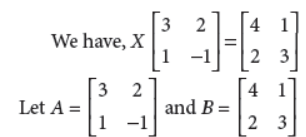
∴ |A| = –3 – 2 = –5 ≠ 0, so A–1 exists.
Now, the given matrix equation is XA = B
∴ X(AA–1) = BA–1 ⇒ X = BA–1
Now, cofactors of matrix A are given by A11 = –1, A12
= –1, A21 = –2, A22 = 3
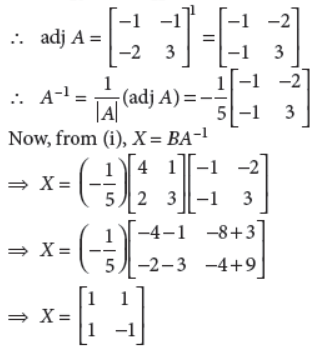
OR
Find the inverse of the matrix
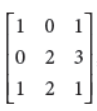
Answer :