Please refer to Matrices MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Matrices will help you to prepare for the exams and get more marks.
Matrices MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Matrices in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Matrices
Question. If (Image 80) then values of x, y, z, w are:
(a) 2, 2, 3, 4
(b) 2, 3, 1, 2
(c) 3, 3, 0, 1
(d) None of these
Answer
A
Question: The system of equations x+Y+3z=1, 2x+y+2z=3 nad 3x+2y+5z=3 have
(a) unique solution
(b) infinite solution
(c) inconsistent
(d) None of these
Answer
C
Question: If A=

and det A3 = 125, then α is equal to
(a) ± 1
(b) ± 2
(c) ± 3
(d) ± 5
Answer
C
Question:

Answer
D
Question:

(a) 2
(b) 4
(c) 6
(d) 3
Answer
A
Question:

Answer
A
Question:


Answer
A
Question:

(a) (14) 2
(b) (13) 2
(c) (14) 3
(d) ( 3) 3
Answer
A
Question: Let

B=A+A2+A3+A4 is
(a) singular
(b) non-singular
(c) symmetric
(d) |B | = 1
Answer
B
Question: 10.//10 If adj B =A and |p|= |Q|=1, then adj (Q-1 BP-1))is equal
(a) APQ
(b) PAQ
(c) B
(d) A
Answer
B
Question: If i = √-1, a = 1 +√5 /2, b = 1- √5/2, then which of the following matrix is idempotent

Answer
C
Question: If A=
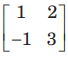
and if A6=KA-2051, then
(a) K = 11
(b) K = 22
(c) K =33
(d) K = 44
Answer
D
Question: If matrix A =

where a ,b and c are real positive number, abc = 1 and AT A= I , then which of the following is/are true.
(a) a+ b+ c = 5
(b) a2+ b2+c2 = 6
(c) ab + bc+ ca = 2
(d) a3+ b3 + c3 = 4
Answer
D
Question:

(a) 2009
(b) -2009
(c) 0
(d) 2008
Answer
A
Question: Matrix Mr is defined as Mr =

value of det (M1)+ det (M2) + det (M3)+…+ det (M2007)is
(a) 2007
(b) 2008
(c) 20082
(d) 20072
Answer
D
Question: The matrices

(a) 27
(b) 7
(c) – 27
(d) – 7
Answer
D
Question: The matrix

is the matrix reflection in the line
(a) x = 1
(b) x + = y 1
(c) y = 1
(d) x =y
Answer
D
Question: The system of simultaneous equations kx+ 2y- z = 1 (k-1) y-2z=2 and (k+2) z=3 has a unique solution, if k is equal to
(a) – 2
(b) – 1
(c) 0
(d) 1
Answer
B
Question: If A =

,B=

then (A+B)-1 is equl to
(a) is a skew-symmetric matrix
(b) A-1 B -1
(c) does not exist
(d) None of the above
Answer
D
Question: If A =

(a) f( -x)
(b) f (x )
(c) – f (x )
(d) – f (-x )
Answer
A
Question: If In is the identity matrix of order n, then (In) -1 is equal to
(a) does not exist
(b) In
(c) 0
(d) n I n
Answer
B
Question: Matrix A such that A2=2A-I is the identity matrix. Then, for n ≥ 2,An is equal to
(a) n A -(n-1)1
(b) n A -I
(c) 2n-1 A- (n-1) I
(d) 2n-1A-1
Answer
A
Question: If 3A=
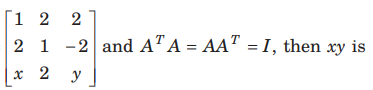
equal to 24
(a) -1
(b) 1
(c) 2
(d) – 2
Answer
C
Question:
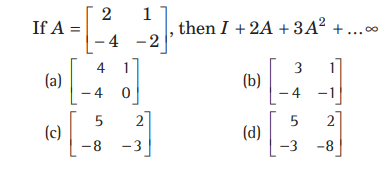
Answer
C
Question:

Answer
C
Question:

then α is equal to
(a) – 2
(b) 5
(c) 2
(d) – 1
Answer
B
Question: If A x =

is an idempotent matrix, then x is equal to
(a) – 5
(b) – 1
(c) – 3
(d) – 4
Answer
C
Question: If A is skew-symmetric and B= (I -A)-1 (I+ A), then B is
(a) singular
(b) symmetric
(c) skew-symmetric
(d) orthogonal
Answer
D
Question:
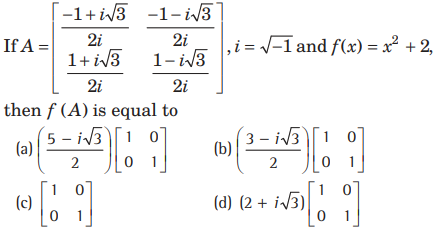
Answer
D
Question: If the matrix

is orthogonal, then
(a) α = ± 1/√2
(b) α = ± 1/ √3
(c) β = ± 1/√6
(d) α=± √3β
Answer
(A,C,D)
Question: If A =

then which of the following are true?
(a) |AT| =1
(b) |A –1| =1
(c) A-1=adj A
(d) |AAT | =10
Answer
(A,B,C)
Question: The values of λ and μ for which the system of equations.
x+ y+z = 6, x+ 2y+3z = 10 and x+ 2y + λz =μ have no solution are
(a) λ =3
(b) μ = 10
(c) λ ≠ 3
d) λ ≠10 .
Answer
(A,B)
Question:

Answer
B
Question: Let A be an orthogonal non-singular matrix of order n, then the determinant of matrix ‘A -In’I,e.,| A- I -n | is equal to
(a) |In-A|
(b) | A |
(c) |A|| In -A|
(d) (-1 )n |A | |In-A|
Answer
C
Question: The element in the first row and third column of the

(a) – 2
(b) 0
(c) 1
(d) 7
Answer
D
Question:

Answer
D
Question:

Answer
B
Question: The values of x, y, z in order, if the system of equations 3x +y 2z=3, 2x-3y-z=-3 and x + 2y+ z = 4 has unique solution, are
(a) 2, 1, 5
(b) 1, 1, 1
(c) 1, -2, -1
(d) 1, 2, -1
Answer
D
Question: By elementary transformation method, the inverse

Answer
A
Question:

Answer
D
Question: The system of equations
(aα +b)x + ay +bz=0
(bα +c)x + by + cz=0
(aα+b)+ (bα+c)z=0
has a non-trival solution, if
(a) a, b, c are in AP
(b) a, b, c are in GP
(c) a, b, c are in HP
(d) α is not a root of ax2+ 2bx+c=0
Answer
B
Question: The system of equations
αx +y +z= α-1
x+α y + z=α-1
x+ y +α z= α-1
has no solution, if a is
(a) not -2
(b) 1
(c) -2
(d) either -2 or 1
Answer
C
Question: The number of solutions of the system of equations
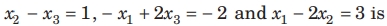
(a) zero
(b) one
(c) two
(d) infinite
Answer
A
Question:

Answer
B
Question: The values of a for which the system of equations
x +y +z=1
x+2y+4z=α
x +4y + 10z=α2
is consistent, are
(a) 1, 2
(b) – 1, 2
(c) 1, 2
(d) None of these
Answer
C
Question: Total number of possible matrices of order 3 x 3 with each entry 2 or 0 is
(a) 9
(b) 27
(c) 81
(d) 512
Answer
D
Question:

Answer
A
Question:

Answer
C
Question: If I is a unit matrix of order 10,then the determinant of I is equal to
(a) 10
(b) 1
(c) 1/10
(d) 9
Answer
B
Question: If A and B are square matrices of order 3, then

Answer
B
Question:

Answer
B
Question:

Answer
A
Question. The system of linear equation x +y + z =2 , 2x + y − z = 3, 3x + 2y + k z = 4 has unique solution if:
(a) K ≠ 0
(b) –1 < K < 1
(c) –2 < K < 2
(d) K = 0
Answer
A
Question. The rank of the matrix (Image 80) is:
(a) 1 if a = 6
(b) 2 if a =1
(c) 3 if a = 2
(d) 1 if a = – 6
Answer
B,D
Question. If one of the Eigen values of a square matrix A order 3×3 is zero, then prove that det A = 0?
(a) A = 0
(b) A ≠ 0
(c) A < 2
(d) K = 0
Answer
A
Question. If A and B are square matrices of order n×n, then 2 (A − B) is equal to :
a. A2 − B2
b. A2 − 2AB + B2
c. A2 + 2AB + B2
d. A2 − AB − BA + B2
Answer
D
Question. If [aij] A = a is a scalar matrix then trace of A is:

Answer
D
Question. Matrix

is invertible for:
a. K =1
b. K = −1
c. K = 0
d. All real K
Answer
D
Question. Let

where α∈R, then [ f (α )]−1 is equal to:
a. f (−α )
b. 1 f (α − )
c. f (2α )
d. None
Answer
A
Question. If

a. α = a2 + b2 ,β = ab
b. α = a2 + b2 ,β = 2ab
c. α = a2 + b2 ,β = a2 – b2
d. α = 2ab , β = a2 – b2
Answer
B
Question. Let

Then F (α ).F (α ‘) is equal to:
a. F (αα ‘)
b. F (α /α ‘)
c. F (α +α ‘)
d. F (α −α ‘)
Answer
C
Question. A square matrix A = [aij] in which aij = 0 for i ≠ j and ae = k (constant) for i = j is called a:
a. Unit matrix
b. Scalar matrix
c. Null matrix
d. Diagonal matrix
Answer
B
Question. For the matrix

which of the following is correct:
a. A3 + 3A2 − I = 0
b. A3 − 3A2 − I = 0
c. A3 − 2A2 − I = 0
d. A3 − A2 + I = 0
Answer
B
Question. The matrix

is known as:
a. Upper triangular matrix
b. Skew-symmetric matrix
c. Symmetric matrix
d. Diagonal matrix
Answer
B
Question. Inverse of diagonal matrix (if it exists) is a:
a. Skew-symmetric matrix
b. Diagonal matrix
c. Non invertible matrix
d. None of these
Answer
B
Question. If A and B are square matrices of same order then:
a. (AB)′ = A′B′
b. (AB)′ = B′A′
c. AB = 0, if | A|= 0 or | B |= 0
d. AB = 0, if | A|= I or B = I
Answer
B
Question. If

then which of the following statement is not correct:
a. A is orthogonal matrix
b. T A is orthogonal matrix
c. Determinant A =1
d. A is not invertible
Answer
D
Question. If

then | adj A| is equal to:
a. 16
b. 10
c. 6
d. 11
Answer
B
Question. In an upper triangular matrix n × n, minimum number of zeros is:
a. n(n–1)/2
b. n(n+1)/2
c. 2n(n–1)/2
d. None of these
Answer
A
Question. Let

If B is the inverse of matrix A, then α is:
a. 5
b. –1
c. 2
d. –2
Answer
A
Question. If


Answer
C
Question. Let p be a non-singular matrix, 1 + p + p2+. . .pn = 0 (0 denotes the null matrix), then 1 p− = ?
a. pn
b. − pn
c. (1 ….. ) n − + p + + p
d. None of these
Answer
A
Question. The rank of the matrix

a. 2
b. 3
c. 1
d. 4
Answer
A
Question. Matrix A is such that 2 A = 2A− I where I is the identity matrix. Then for 2, n n ≥ A = ?
a. nA− (n −1)I
b. nA− I
c. 2n-1 A − (n −1)I
d. 2n-1 A−I
Answer
A


