Please refer to Class 12 Mathematics Sample Paper Term 2 Set B with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
CBSE Class 12 Mathematics Sample Paper for Term 2
Section – A
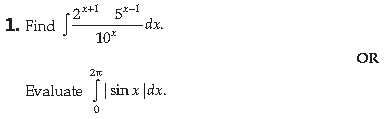
Answer.
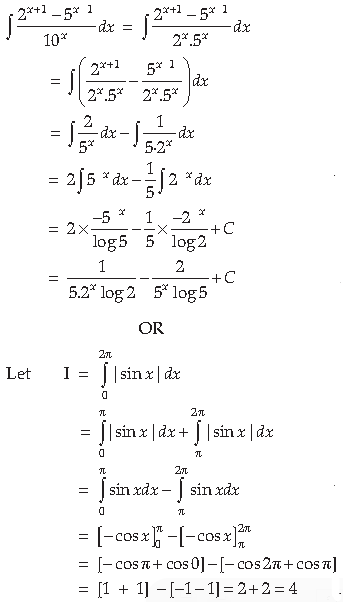
2. Find the general solution of the differential equation dy/dx = ex+y .
Answer.
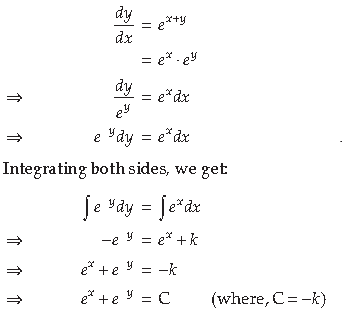
3. Let a̅ and b̅ be two-unit vectors and q be the angle between them. Then for what value of θ, a̅, + b̅ is a unit vector.
Answer. Let a̅ and b̅ be two-unit vectors and θ be the angle between them
4. Find the cartesian equation of the line which passes through the point (– 2, 4, – 5) and is parallel to the line

Answer.

[If two lines are parallel, then they both have proportional direction ratio]

Here, given point is (– 2, 4, – 5) with D.R’s. 3, – 5, 6
Therefore, cartesian equation of parallel line will be :

5. A refrigerator box contains 2 milk chocolates and 4 dark chocolates. Two chocolates are drawn at
random. Find the probability distribution of the number of milk chocolates. What is the most likely
outcome?
Answer.
Let X denote the number of milk chocolates drawn
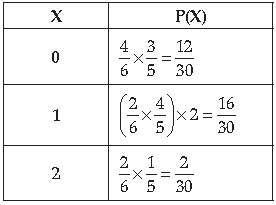
Most likely outcome is getting one chocolate of each type.
6. If P(not A) = 0.7, P(B) = 0.7 and P (B/A) = 0.5, then find P (A/B)
Answer. P(A̅) = 0.7 Þ1 – P(A) = 0.7 Þ P(A) = 0.3
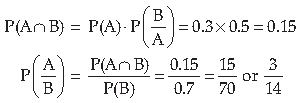
Section – B
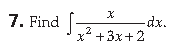
Answer.
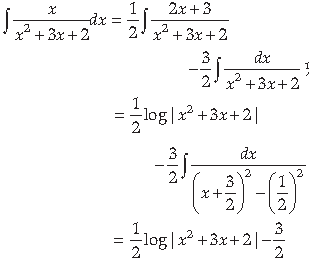

8. Find the particular solution of the differential equation
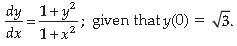
OR
Prove that x2 – y2 = C(x2 + y2)2 is the general solution of the differential equation (x3 – 3xy2) dx =
(y3 – 3x2y) dy, where C is a parameter.
Answer. From the given, equation.
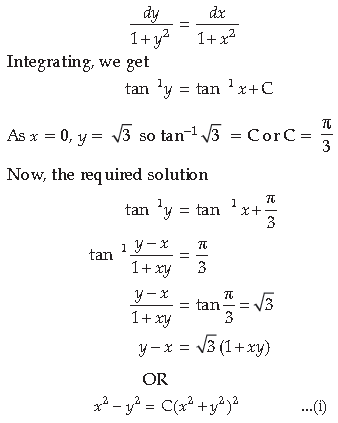
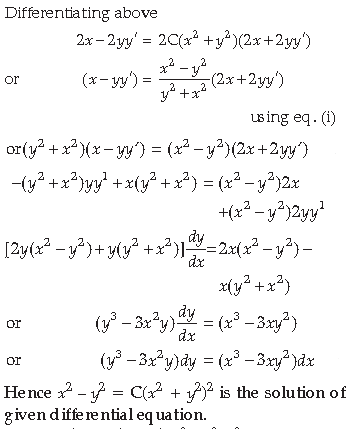
9. If î + ĵ + k̂, 2î + 5ĵ, 3î + 2ĵ – 3k̂ and î – 6ĵ – k̂ respectively are the position vectors of points A, B, C and
D, then find the angle between the straight lines AB and CD. Find whether
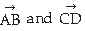
are collinear or not.
OR
Find the area of the quadrilateral ABCD, where A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2).
Answer.

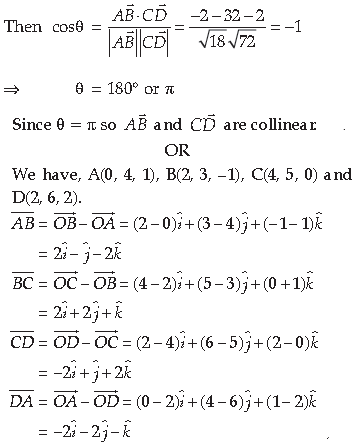

10. If the lines

are perpendicular, find the value of l. Hence find whether the lines are intersecting or not.
Answer. The equations of the given lines are:

Þ –9λ+ 4λ – 10 = 0
Þ –5λ – 10 = 0
Þ –5λ = 10
Þ λ = –2
Hence, for λ = –2 the given lines are perpendicular.
Now, given lines can be written as after substituting value of λ = –2

So, the coordinates of a general point on second line are (–6s + 1, 2s + 1, –5s + 6)
If the lines intersect, then they have a common point. So, for some value of l and m, we must have
–3r + 1 = –6s + 1, –4r + 2 = 2s + 1, 2r + 3
= –5s + 6
or r = 2s, –4r – 2s = –1, 2r + 5s = 3
Solving first two of these two equations, we get r = 1/5and s = 1/10. These values of r and s do
not satisfy the third equation.
Hence, the given lines do not intersect
Section – C
11. Show that:
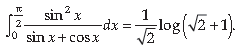
Answer.

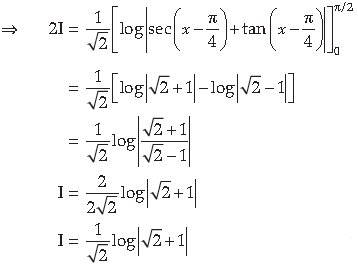
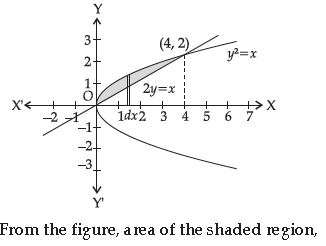
12. Find the area of the region bounded by the parabola y2 = x and the line 2y = x.
OR
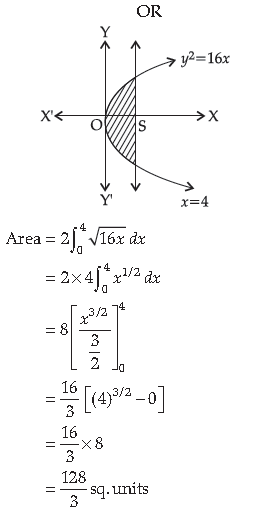
Find the area of the region bounded by the parabola y2 = 16x and the line x = 4.
Answer. When y2 =x and 2y = x
Solving we get y2 =2y
⇒ y = 0, 2 and when y = 2, x = 4 and y = 0 ⇒x = 0
So, points of intersection are (0, 0) and (4, 2). 1
Graphs of parabola y2 = x and 2y = x are as shown in the adjoining figure :

Parabola y2 = 16x and line x = 4
at x = 4, y2 = 64 ⇒ y = ± 8
Hence, the point of intersection (4, 8) and (4, –8)
13. If a̅, b̅, c̅, are unit vectors such that a̅ · b̅, = c̅ · a̅ = 0 and the angle between b̅, and c̅ is π/6 then prove that: a̅ = ± 2 (b̅ x c̅)
Answer. As given
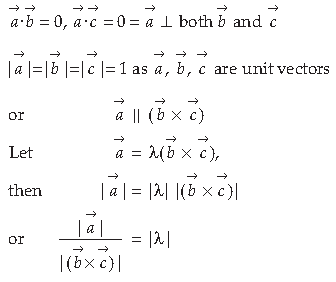
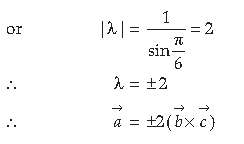
Case-Based/Data Based
14. Bag I contains 1 white, 2 black and 3 red balls; Bag II contains 2 white, 1 black and 1 red balls; Bag III
contains 4 white, 3 black and 2 red balls. A bag is chosen at random and two balls are drawn from it
with replacement. They happen to be one white and one red.

Based on the above information, answer the following questions:
(i) What is the probability that they came from Bag III?
(ii) What is the probability that they will come from Bag I?
Answer. Let E1 = Bag I is chosen, E2 = Bag II is chosen, E3 = Bag III is chosen, A = The two balls drawn from the chosen bag are one white and one red.


