Please refer to Class 12 Mathematics Sample Paper Term 1 Set C with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
CBSE Class 12 Mathematics Sample Paper for Term 1
SECTION-A
In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.
1. The principal value of cos -1(-1/√2) + 2sin -1(1/√2) is
(A) π/4
(B) 5π/4
(C) 3π/2
(D) π/2
Answer
B
2. The points of discontinuity of f, where f is defined by
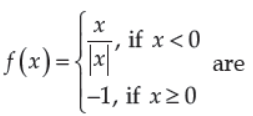
(A) x = 1
(B) x = –1
(C) x = 0
(D) no point of discontinuity
Answer
D
3. A =

(A) A
(B) A’
(C) I
(D) A2
Answer
C
4. The minor of element 6 in the determinant
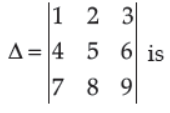
(A) 6
(B) –4
(C) 8
(D) –6
Answer
D
5. The intervals in which the function f given by f(x) = 2x2 – 3x is strictly decreasing is:
(A) (-∞ , 3/4)
(B) (3/4 ,∞)
(C) (–∞, 3)
(D) (1, ∞)
Answer
A
6. Given that A is a square matrix of order 3 and |A| = –2 then|adj A| is
(A) 9
(B) 16
(C) 4
(D) –4
Answer
C
7. Show that the relation R in the set Z of integers given by R = {(a, b) : 2 divides a – b} is an/a
(A) equivalence relation
(B) symmetric only
(C) Reflexive only
(D) None of these
Answer
A
8. If
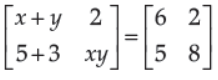
then the possible values of x, y and z are
(A) 4, 2, 0
(B) 2, 4, 0
(C) 1, 1, 2
(D) Both (A) and (B)
Answer
D
9. The point at which the tangent to the curve y =√4x -3-1 has its slope 2/3 .
(A) (2, 3)
(B) (3, 3)
(C) (3, 2)
(D) (2, 2)
Answer
C
10. The principal Value of sec-1(2/√3) is
(A) π/4
(B) π/3
(C) π/6
(D) π/2
Answer
C
11. The relation R in the set (1, 2, 3} given by R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)} is
(A) reflexive and symmetric
(B) transitive
(C) neither reflexive nor symmetric
(D) reflexive but neither symmetric nor transitive
Answer
D
12. If x and y are connected parametrically by the equation x = 2at2, y = at4 then dy/dx will be
(A) t2
(B) t3
(C) a2
(D) 1
Answer
A
13. Given matrix A and B are of order 3 × n and m × 6 respectively, then the order of matrix C = 5A + 2B
(A) 3 × 5 and m = n
(B) 3 × 6 and n = m
(C) 3 × 6
(D) 3 × 5
Answer
B
14. The second order derivatives of the function y = x20 is:
(A) 38x18
(B) 20x18
(C) 380x18
(D) x18
Answer
C
15. For matrix A =
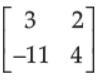
, (adjA)’ is equal to

Answer
A
16. Point on the curve at x2/4 + y2/25 = 1
at which the tangents are parallel to y-axis are :
(A) (±5, 0)
(B) (0, ±5)
(C) (0, ±2)
(D) (±2, 0)
Answer
D
17. A square matrix A is invertible if and only if A is
(A) Singular matrix
(B) Non-singular matrix
(C) Null matrix
(D) None of these
Answer
B
18. If y = ex/sin x then dy/dx will be,

Answer
A
19. The feasible region determined by the system of constraints, x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, and y ≥ 0, is as follows. If Z = –3x + 4y then minimum value of Z is
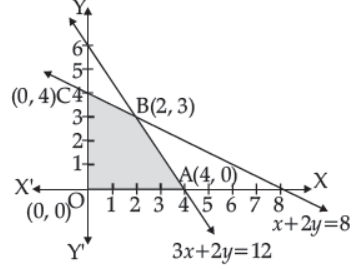
(A) 0
(B) –12
(C) 16
(D) 6
Answer
B
20. Find the intervals in which the function f given by f(x) = x2 – 4x + 6 is increasing.
(A) (2, ∞)
(B) (–∞, 2)
(C) (0, 1)
(D) None of these
Answer
A
SECTION-B
In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.
21. An onto function f : {1, 2, 3} → {1, 2, 3} is
(A) One-one
(B) always one-one
(C) bijective
(D) None of these
Answer
B
22. The second order derivatives of the function e6x cos 3x is:
(A) 9e6x(3 cos3x + 4sin3x)
(B) 9e6x(3 cos 3x + 4sin3x)
(C) 9e6x(4 sin3x + 4cos3x)
(D) 9ex(3 cosx + 4sin3x)
Answer
B
23. The feasible region determined by the system of constraints, 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, and y ≥ 0, are as follows.
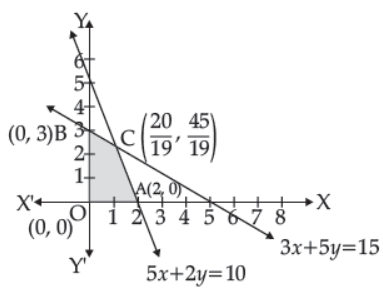
If Z = 5x + 3y then at which point Z will be maximum
(A) (0, 0)
(B) (2, 0)
(C) (0, 3)
(D) (20/190) , (45/19)
Answer
D
24. If y = 500e7x + 600e–7x, then d2y/dx2 will be
(A) 9y
(B) 7y
(C) 41y
(D) 49y
Answer
D
25. If A =
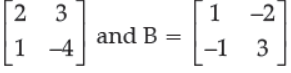
, then (AB)–1 will be

Answer
C
26. The intervals in which the function f given by f(x) = sinx + cosx, 0 ≤ x ≤ 2π is decreasing is:
(A) (π/2 , π)
(B) (π/2 , 5π)
(C) (0 , π/4)
(D) (0 , π/2)
Answer
B
27. The value of cos-1(1/2) + sin -1(1/2) will be
(A) 2π/3
(B) π/3
(C) -2π/3
(D) 4π/3
Answer
A
28. Given that A is a non-singular matrix of order 3 that A2 = 3A then value of |3A| is
(A) 729
(B) 27
(C) 81
(D) 64
Answer
A
29. The equations of the tangent and normal to the curve x2/3 + y2/3 = 2at (1,1) are
(A) y + x –2 = 0, y – x = 0
(B) x + y = 0, y + x – 1 = 0
(C) x – y = 1, x + y = 2
(D) y + x –1 = 0, x + y = 0
Answer
A
30. A ono-one function f : {1, 2, 3} → {1, 2, 3} must be
(A) Bijective
(B) Onto
(C) Null
(D) None of these
Answer
B
31. The relationship between a and b so that the function f defined by:
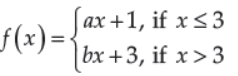
(A) a = b + 2
(B) a = b +2/3
(C) a = b -2/3
(D) a = b
Answer
B
32. The value of a, b, c and d from the equation
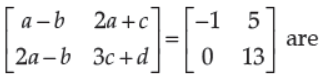
(A) 1, 2, 3, 4
(B) 4, 2, 3, 1
(C) 2, 3, 1, 4
(D) 4, 3, 2, 1
Answer
A
33. A linear programming problem is one that is concerned with finding the optimal value (maximum or minimum) of a linear function of several variables (called objective function) subject to the conditions that the variables are non-negative and satisfy a set of linear inequalities (called linear constraints).
Variables are sometimes called ___________ and are non-negative.
(A) Decision variable
(B) Random variable
(C) Constant
(D) None of these
Answer
A
34. The function given by f(x) = log x/x has maximum at
(A) x = 1
(B) x = e2
(C) x = –e
(D) x = e
Answer
D
35. If
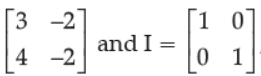
, and A2 = kA – 2I then k is equal to
(A) –1
(B) 1
(C) 2
(D) 0
Answer
B
36. The principal value of cos -1(√3) + cot -1(1/√3) is :
(A) π/2
(B) -π/6
(C) π/3
(D) -π/3
Answer
A
37. Show that the function f : N → N, given by f(1) = f(2) = 1 and f(x) = x – 1, for every x > 2, is
(A) Onto
(B) One-one but not onto
(C) Onto but not one-one
(D) One-one and onto
Answer
C
38. If A =


Answer
C
39. The equation of tangent to the curve given by x = a sin3t, y = b cos3t at a point where t = π/2 is
(A) y = 2
(B) y = 0
(C) y = 1
(D) y = –1
Answer
B
40. If matrix A =
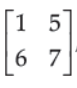
,then (A – A’) is a
(A) Symmetric matrix
(B) Skew symmetric matrix
(C) Null matrix
(D) Both (A) and (B)
Answer
B
SECTION-C
In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.
41. The feasible region determined by the constraints, 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, and y ≥ 0, is as follows.
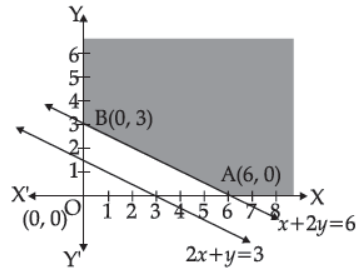
If Z = x + 2y then the Z will be minimum at.
(A) (6, 3) only
(B) (6, 0) only
(C) (0, 3) only
(D) at every point on the line x + 2y = 6
Answer
D
42. The slope of the tangent to curve y = x3 – x + 1 at the point whose x-coordinate is 2 is:
(A) 12
(B) 11
(C) 2
(D) –2
Answer
B
43. The normal at the point (1, 1) on the curve 2y + x2 = 3 is
(A) x + y = 0
(B) x – y = 0
(C) x + y + 1 = 0
(D) x – y = 1
Answer
B
44. The common region determined by all the constraints including the non-negative constraints x ≥ 0, y ≥ 0 of a linear programming problem is called the region (or solution region) fot the problem.
(A) Infeasible region
(B) Feasible region
(C) Neither feasible nor infeasible region
(D) None of these
Answer
B
45. For the matrix A =

, find the numbers a and b such that A2 + aA + bI = O.
(A) –4, –1
(B) –4 ,1
(C) 1, 3
(D) 4, 4
Answer
B
CASE-STUDY
A water tank has the shape of an inverted right circular cone with its axis vertical and vertex lowermost.
Its semi-vertical angle is tan–1 (0.5). Water is poured into at a constant rate of 5 cubic metre per hour.
Find the rate at which the level of the water is rising at the instant when the depth of water in the tank is 4 m.
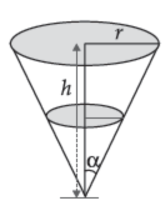
46. It r be the radius, h be the height and a be the semi-vertical angle then the relation between h and r is
(A) r = 2h
(B) r =h/2
(C) r = h
(D) 3r = h
Answer
B
47. Volume of the cone in term of h is given by
(A) πh3/12
(B) 5πh3/12
(C) πh3/6
(D) πh3/3
Answer
A
48. First derivative of V w.r.t t is (in term of h)
(A) 3π/4 h2 dh/dt
(B) 1/4 πh2 dh/dt
(C) πh2 dh/dt
(D) π/3 h2 dh/dt
Answer
B
49. The rate of change of water level is
(A) 35/11 m/h
(B) 35/44 m/h
(C) 35/88 m/h
(D) 35/22 m/h
Answer
C
50. Which mathematical concept used in this case-study.
(A) Matrix
(B) LPP
(C) Vector
(D) Application of derivatives
Answer
D
