Please refer to Class 12 Mathematics Sample Paper Set J with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
SECTION A
1. Evaluate : sin (2 cos-1(-3/5)) .
Solution: – 24/25
2. State the reason for the following Binary Operation *, defined on the set Z of integers, to be not commutative : a*b = ab3.
Solution: Note that 1*2 =1×23 = 8 but 2*1 = 2×13 = 2 ≠ 1*2 where 1, 2 ∈ Z . So * isn’t commutative.
3. Give an example of a skew symmetric matrix of order 3.
Solution: 3
4. Using derivatives, find the approximate percentage increase in the area of a circle if its radius is increased by 2%.
Solution: 4%.
5. Find the derivative of f (etan x ) w.r.t. x at x = 0 . It is given that f ‘(1) = 5 .
Solution: 5.
6. If the lines x-1/-2 = y-4/3p = z-3/4 and x-2/4p = y-5/2 = z-1/-7 are perpendicular to each other then, find the value of p.
Solution: –14.
SECTION B
7. Let f :W → W be defined as f(n) =
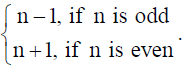
Then show that f is invertible. Also find the inverse of f.
Solution: Here fof :W → W is such that if n is odd, fof (n) = f (f (n)) = f (n -1) = n -1+1 = n and if n is
even, fof (n) = f (f (n)) = f (n +1) = n +1-1 = n .
Hence fof = I. This implies that f is invertible and f –1 = f.
OR
Show that the relation R in the set N → N defined by (a, b)R(c,d) iff a2 + d2 = b2 + c2 ∀ a, b,c,d ∈ N , is an equivalence relation.
Solution: Let (a, b)∈ NxN. Then as a2 + b2 = b2 + a2 ∴ (a, b)R(a, b) . So, R is reflexive.
Let (a, b), (c,d)∈ NxN be s.t. (a, b)R(c,d). Then as a2 + d2 = b2 + c2 ⇒ c2 + b2 = d2 + a2
∴ (c,d)R(a, b) . So R is symmetric.
Let (a, b), (c,d), (e, f )∈ NxN be s.t. (a,b)R(c,d) and (c,d)R(e, f ).
Then as a2 + d2 = b2 + c2 and c2 + f2 = d2 + e2 ⇒ a2 + d2 + c2 + f2 = b2 + c2 + d2 + e2
⇒ a2 + f 2 = b2 + e2 ∴ (a, b)R(e,f ) . So R is transitive.
Since R is reflexive, symmetric as well as transitive so, R is an equivalence relation.
8. Prove that tan-1(√1+cos x √1-cos x/√1+cos x – √1-cos x) = π/4 – x/2 , where π <x< 3π/2 .
Solution:
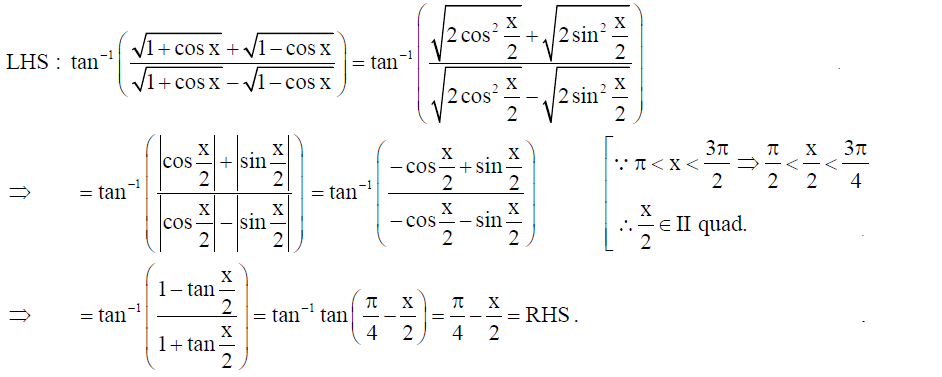
9. Let
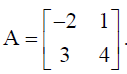
Then verify A(adjA) = (adjA)A = | A | I , where I is the identity matrix of order 2.
Solution:
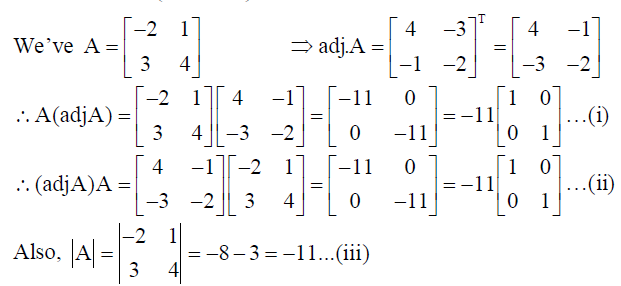
By (i), (ii) & (iii), A(adjA) = (adjA)A = | A | I is verified.
10. Using properties of determinants, prove that
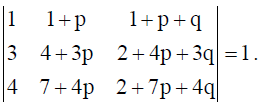
Solution:
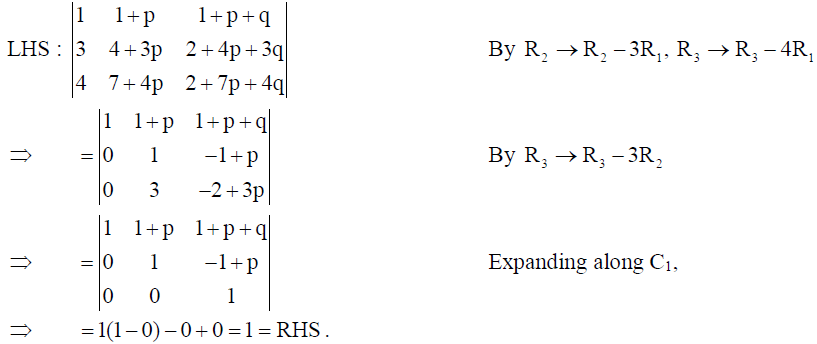
OR
Without expanding the determinant at any stage, prove that

Solution:
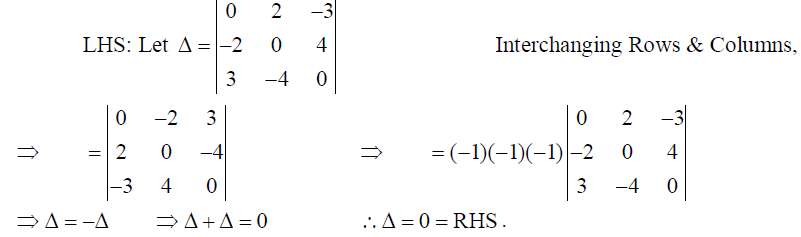
11. Let A =
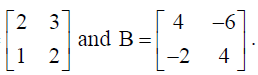
Then compute AB. Hence, solve the following system of equations : 2x + y = 4, 3x + 2y =1.
Solution:

12. If the following function is differentiable at x = 2, then find the value of a and b :
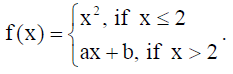
Solution: As the function f is differentiable at x = 2, so it is continuous at x = 2 as well.
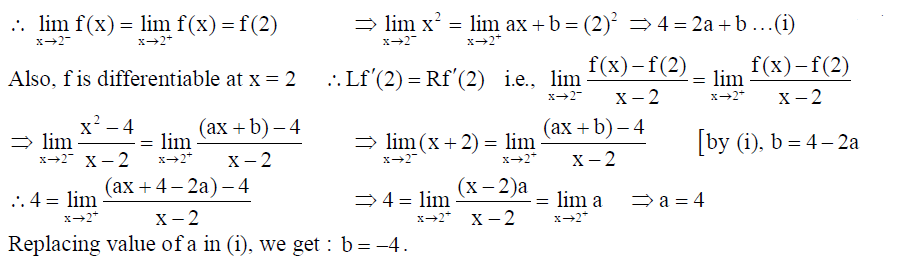
13. Let y = (log x)x + xx cos x . Then find dy/dx .
Solution: We have y = (log x)x = xx cos x .
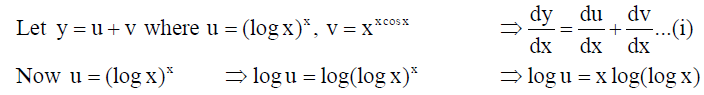
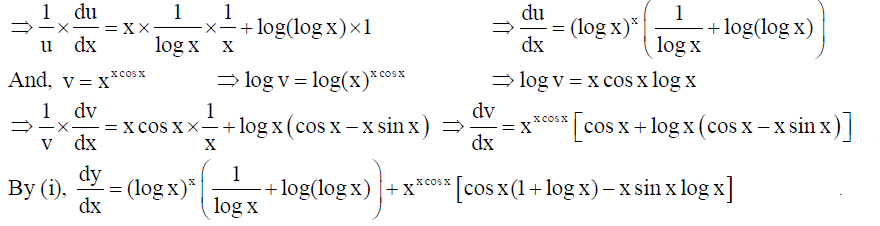
OR
If x = a sin pt and, y = b cos pt . Then find d2y/dx2 at t = 0 .
Solution: We have x = a sin pt and, y = b cos pt ⇒ dx/dt = ap cos pt and, dy/dt = -bp sin pt
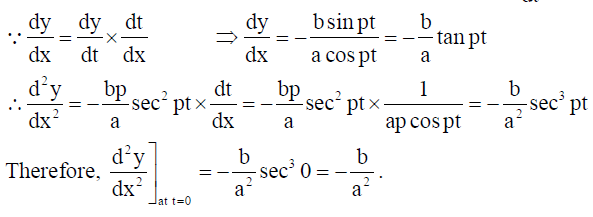
14. Evaluate :
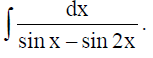
Solution:
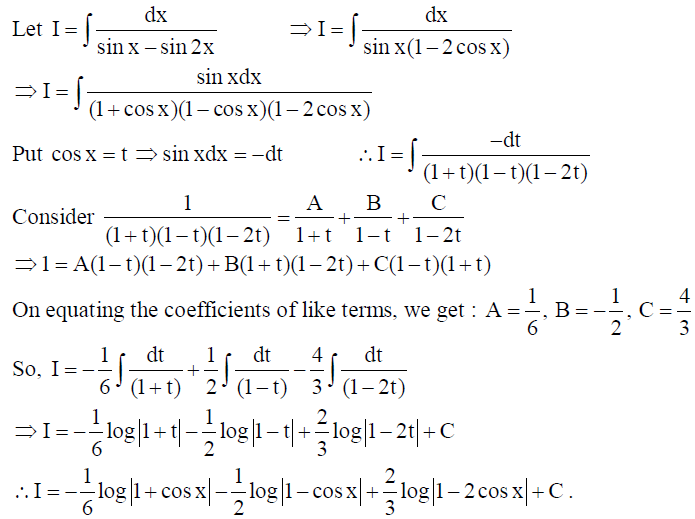
OR
Evaluate :

Solution:
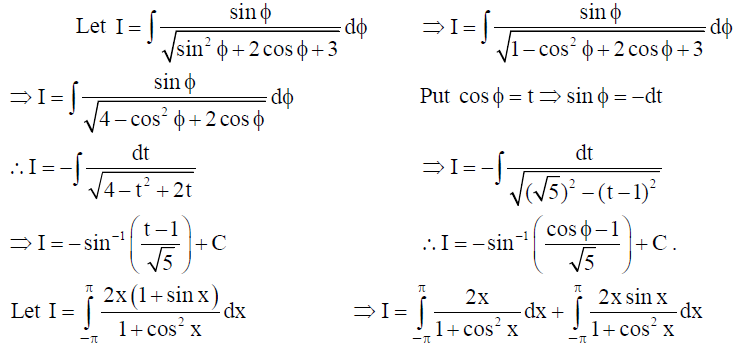
15. Evaluate the definite integral :
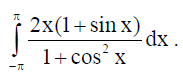
Solution:
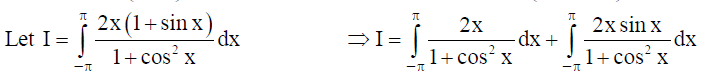

16. Solve : dy/dx = y/x + √x2+y2/x , x > 0 .
Solution: We have dy/dx = y/x + √x2+y2/x , x > 0 ..(i)
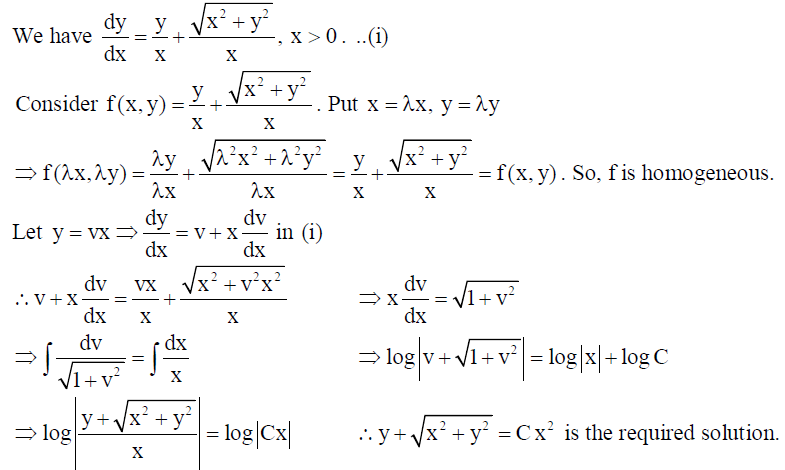
17. Solve : (1+ y2 )dx = (tan-1 y – x)dy .
Solution: Given that (1+ y2 )dx = (tan-1 y – x)dy ⇒ dx/dy = tan-1 y/1+y2 – x/1+y2
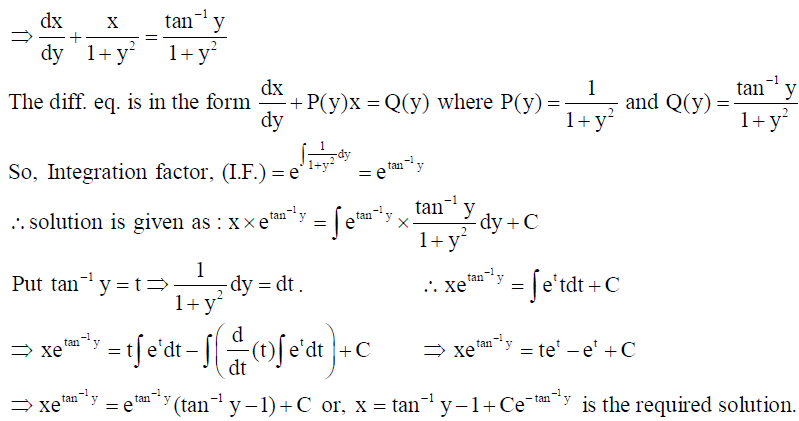
18. Find the shortest distance between the following pair of skew lines :
x-1/2 = 2-y/3 = z+1/4 and x+2/-1 = y-3/2 = z/3 .
Solution: The lines in vector form can be written as :
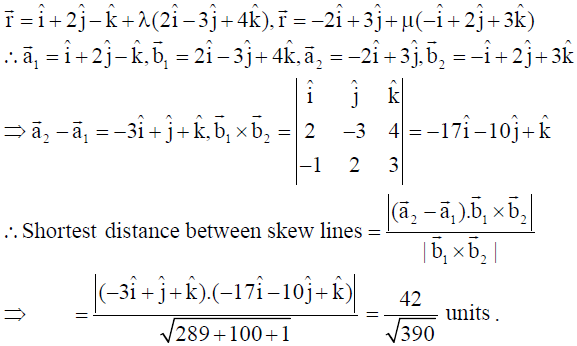
19. A problem in Mathematics is given to 4 students A, B, C and D. Their chances of solving the problems respectively are 1/3, 1/4, 1/5 and 2/3. What is the probability that (i) the problem will be solved? (ii) at most one of them will solve the problem?
Solution: Let A, B, C and D denote the events that A, B, C and D solves the problem in Mathematics respectively.

SECTION C
20. Find the intervals in which the following function is strictly increasing or strictly decreasing.
Also find the points of local maximum and local minimum, if any : f (x) = (x -1)3 (x + 2)2 .
Solution: Given f (x) = (x -1)3 (x + 2)2
∴ f ‘(x) = (x -1)2 (x + 2)(5x + 4)
For critical points, f ‘(x) = 0
⇒ (x -1)2 (x + 2)(5x + 4) = 0
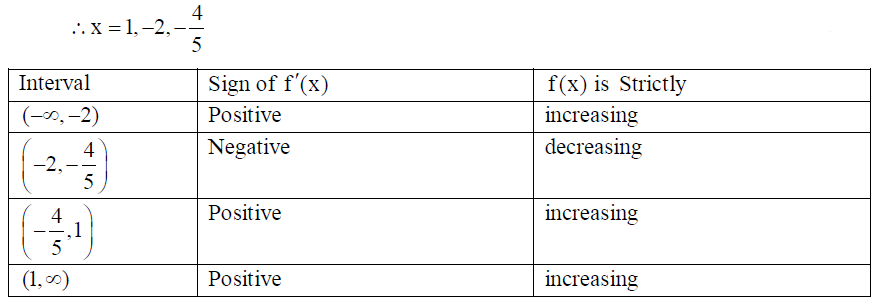
Hence f is strictly increasing in ( -∞, 2) and (-4/5 , ∞) & strictly decreasing in (-2 , -4/5) . Also in the left neighbourhood of –2, f ‘(x) is positive and in right neighbourhood of –2, f ‘(x) is negative and f ‘(-2) = 0 . Therefore by the first derivative test, x = –2 is a point of local maximum.
Also f ‘(x) changes its sign from negative to positive as x passes through –4/5 so, x = –4/5 is a
point of local minimum.
21. If a̅, b̅ and c̅ are unit vectors such that a̅.b̅ = a̅.c̅ = 0 and the angle between b̅ and c̅ is π/6 , then prove that (i) a̅ = ±2(b̅ x c̅ ) (ii) [a̅ + b̅ b̅ + c̅ c̅+a̅] = ± 1 .
Solution: Given that a̅.b̅ = a̅.c̅ = 0 which implies, a̅ is perpendicular to both b̅ and c̅ (since these three vectors are unit vectors). That is, a̅||b̅ x c̅ ⇒ a̅ = λ(b̅ x c̅)
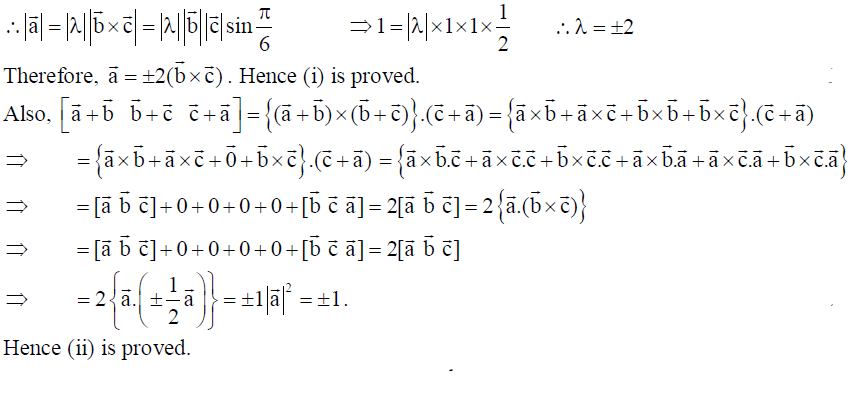
22. Using integration, find the area bounded by the tangent to the curve 4y = x2 at the point (2, 1) and the lines whose equations are x = 2y and x = 3y -3 .
Solution:

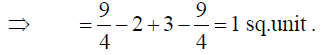
23. Find the distance of the point 3î – 2ĵ + k̂ from the plane 3x + y – z + 2 = 0 measured parallel to the x-1/2 = y+2/-3 = z-1/1 . Also find the foot of perpendicular from the given point upon the given plane.
Solution: The equation of line through 3î – 2ĵ + k̂i.e., P(3, –2, 1) and parallel to the given line having d.r.’s as (2, –3, 1), is x-1/2 = y+2/-3 = z-1/1 .
The coordinates of any random point on this line is : A(2λ + 3,-3λ – 2,λ +1)
If A lies on the plane 3x + y – z + 2 = 0 , then 3(2λ + 3) + (-3λ – 2) – (λ +1) + 2 = 0 ⇒ λ = -4 Therefore, A(–5, 10, –3).
Hence, the required distance is, AP = √(3+ 5)2 + (-2 -10)2 + (1+ 3)2 = 4 √14 units .
Now, the equation of line passing through P(3, –2, 1) and perpendicular to the given equation of plane 3x + y – z + 2 = 0 is, x-3/3 = y+2/1 = z-1/-1
The coordinates of any random point on this line is : B(3μ + 3,μ – 2,-μ +1)
If B lies on the plane 3x + y – z + 2 = 0 , then 3(3μ + 3) + (μ-2) – (-μ + 1) + 2 = 0 ⇒ μ = – 8/11
Therefore, the required foot of perpendicular is (9/11 , 30/11 , 19/11) .
OR
Find the equation of the plane passing through the line of intersection of the planes r̅.(2î + 3ĵ – k̂) and r̅.(î + ĵ – 2k̂) = 0 and passing through the point (3, –2, –1). Also find the angle between the two given planes.
Solution: Any plane passing through the line of intersection of given planes is
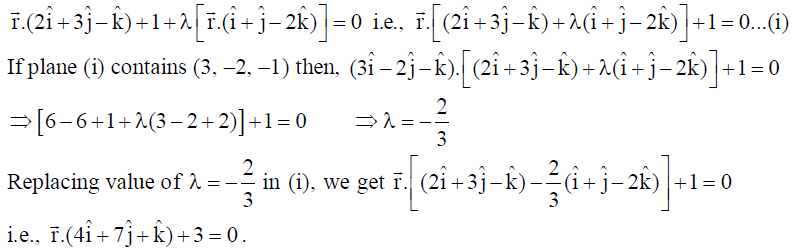
Let θ be the angle between normals of the given planes (as angle between the planes and their
normals remains the same).

24. A Bag I contains 5 red and 4 white balls and a Bag II contains 3 red and 3 white balls. Two balls are transferred from the Bag I to the Bag II and then one ball is drawn from the Bag II. If the ball drawn from the Bag II is red, then find the probability that one red ball and one white ball are transferred from Bag I to the Bag II.
Solution: Let E1 : 2 white balls are transferred from Bag I to the Bag II, E2 : 2 red balls are transferred
from Bag I to the Bag II, E3 : 1 red and 1 white balls are transferred from Bag I to the Bag II, E :
the ball drawn from Bag II is red.
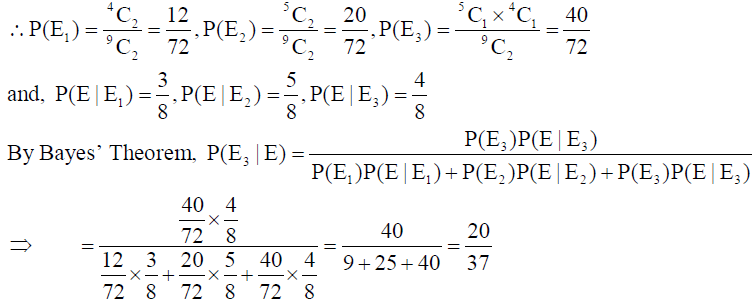
OR
Find the mean, the variance and the standard deviation of the number of doublets in three throws of a pair of dice.
Solution: Let X : number of doublets in three throws of a pair of dice. ∴ X = 0,1,2,3.
Here n = 3. Let p be the probability of success ∴ P = 6/36 = 1/6 , q = 1 – p = 5/6

25. A farmer wants to construct a circular garden and a square garden in his field. He wants to keep the sum of their perimeters 600m. Prove that the sum of their areas is the least, when the side of the square garden is double the radius of the circular garden.
Do you think that a good planning can save energy, time and money?
Solution: Let the radius of circular garden be r (in metres) and the side of the square garden be x (in metres).
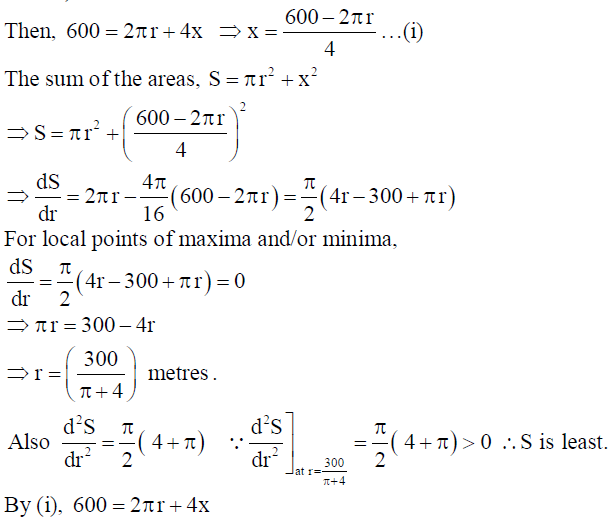

Therefore, when the side of the square garden is double the radius of the circular garden, the sum of their areas is least.
To achieve any goal, there is every possibility that energy, time and money are required to be invested. One must plan in such a manner that least energy, time and money are spent. A good planning and execution, therefore, is essentially needed.
26. A manufacturing company makes two models A and B of a product. Each piece of model A requires 9 hours of labour for fabricating and 1 hour for finishing. Each piece of model B requires 12 hours of labour for fabricating and 3 hours for finishing. The maximum number of labour hours, available for fabricating and for finishing are 180 and 30 respectively. The company makes a profit of ₹ 8000 and ₹12000 on each piece of model A and B respectively.
How many pieces of each model should be manufactured to get maximum profit? Also, find the maximum profit.
Solution: Let the number of pieces of model A and model B respectively be x and y.
To maximize : Z = ₹ (8000x +12000y)
Subject to the constraints : 9x + 12y ≤ 180, x + 3y ≤ 30, x ≥ 0, y ≥ 0
That is, 3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0

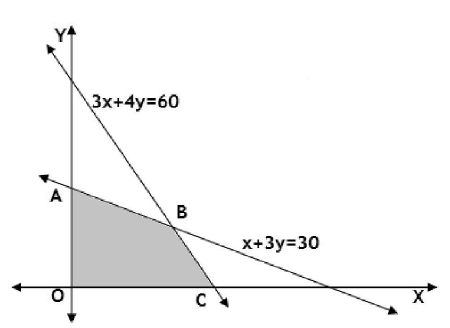
The number of pieces of model A and model B are 12 and 6 respectively.
Also maximum profit is of ₹ 168000.