Please refer to Class 12 Mathematics Sample Paper Term 1 Set A with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
CBSE Class 12 Mathematics Sample Paper for Term 1
SECTION-A
In this section, attempt any 16 questions out of Questions 1 –20.
Each Question is of 1 mark weightage.
1. What is the principal value branch of cot–1x ?
(A) (–1, 1)
(B) [–1, 1]
(C) (0, π)
(D) [0, π]
Answer
C
2. What is the continuity of [x] at x = 3.5 ?
(A) Continuous at the x = 3.5
(B) Continuous at the x = 3.5
(C) Function doesn’t exist
(D) None of the above
Answer
A
3. Choose the correct option for the given matrix.
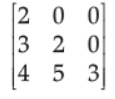
(A) Lower triangular matrix
(B) Upper triangular matrix
(C) Diagonal matrix
(D) Unit matrix
Answer
A
4. If a matrix has 4 rows and 3 columns then how many elements will be there in this matrix?
(A) 4
(B) 3
(C) 1
(D) 12
Answer
D
5. What is the equation of the normal to the curve y = 3x2 – 7x + 5 at (0, 5)?
(A) x – 7y + 35 = 0
(B) 7x – 3y + 35 = 0
(C) 3x + 7y + 35 = 0
(D) 3x + 7y + 21 = 0
Answer
A
6. If A is a square matrix of order 3, such that A(adj A) = 10I, then |adj A| is equal to
(A) 1
(B) 10
(C) 100
(D) 101
Answer
C
7. R be the relation in the set N given by R = {(a, b) : a = b –2, b > 6}. Then, the correct option is:
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
Answer
C
8. Evaluate the determinant of the matrix
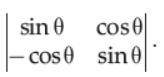
(A) sin q
(B) cos q
(C) 1
(D) 0
Answer
C
9. Which of the function is not differentiable everywhere in R?
(A) log x
(B) sin x
(C) |x|
(D) 3x3 + 5
Answer
C
10. All the trigonometric functions have inverse functions irrespective of the domain.
(A) True
(B) False
(C) True but for only sine, cos and tan
(D) None of the above
Answer
B
11. Let R be the relation in the set {5, 6, 7, 8} given by R = {(5, 6), (6, 6), (5, 5), (8, 8), (5, 7), (7, 7), (7, 6)}.
Choose the correct answer:
(A) R is reflexive and symmetric but not transitive
(B) R is reflexive and transitive but not symmetric
(C) R is symmetric and transitive but not reflexive
(D) R is an equivalence relation
Answer
B
12. What is the equation of the tangent to the curve y – 5x2 = 0 and parallel to line 5x + y + 1 = 0 ?
(A) 20x + 7y + 5 =0
(B) 20x – 3y + = 0
(C) 20x + 4y + 5 = 0
(D) 20x – 9y + 5 = 0
Answer
C
13. If A =
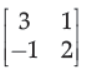
then A2 – 5A + 7I2 is equal to :
(A) 0
(B) 1
(C) -1
(D) 2
Answer
A
14. If y = log(cosex) then dy/dx will be :
(A) x tan ex
(B) ex+tanx
(C) extanex
(D) –ex + tanex
Answer
D
15. For a square matrix A = [aij] the quantity calculated for any element aij in A as the determinant of the square sub-matrix of order (n – 1) obtained by leaving the ith row and jth column of A is known as:
(A) Cofactor
(B) Minor
(C) Coefficient
(D) Elements
Answer
B
16. Which of the following is satisfied by the given function y = sin10x−cos10x ?
(A) d2y/dx2 + 100y = 0
(B) d2y/dx2 + 100y2 = 0
(C) d2y/dx2 – 100y2 = 0
(D) d2y/dx2 – 100y + dy/dx = 0
Answer
A
17. If matrix A = [2 3 5], then the value of A.A’ is:
(A) 38
(B) 26
(C) 39
(D) 28
Answer
A
18. The function y = 5x2 – 32x has a local minimum in the interval (0,10).
(A) x = 1
(B) x = 2
(C) x = 3.2
(D) No local minimum
Answer
C
19. Z = 30x1 + 30x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 3x2≤ 6, 4x1 + 8x2≤ 16, x1 + x2 ≤ 4. The minimum value of Z occurs at
(A) (3, 0)
(B) (2, 1)
(C) (0, 2)
(D) (4, 0)
Answer
C
20. A rectangle of maximum area is inscribed in a circle of radius R.Then which of the following is true?
(A) l = r/2 , b = r/2
(B) l = r/√2 , b = r/√2
(C) l = r/3 , b = r/3
(D) None of the above
Answer
B
SECTION-B
In this section, attempt any 16 questions out of the Questions 21 -40.
Each Question is of 1 mark weightage.
21. Let R be the relation in the set of integers Z given by R = {(a, b) : 3 divides a – b}. then R is :
(A) not reflexive
(B) reflexive
(C) symmetric
(D) transitive.
Answer
A
22. If f(x) = |x|, then the function is continuous but not differentiable at :
(A) x = 0
(B) x ¹ 0
(C) x = 1
(D) x = 2
Answer
A
23. A dietician wishes to mix together two kinds of food X and y in such a way that the mixture contains at least 15 units of carbohydrate, at least 17 units of protein and at most 6 units of fat. The nutrient contents of 1 kg food is given below:

1 kg of food X costs `16 and 1 kg of food Y cost `20. Find the least cost of the mixture which will produce the required diet.
(A) 100
(B) 128
(C) 110
(D) 99
Answer
A
24. What is the domain of the cosec–1x ?
(A) [– ∞, ∞]
(B) (– ∞, ∞)
(C) (– 1, 1)
(D) (– ∞, – 1] ∈ [1, ∞)
Answer
D
25. For a given matrix A=

, both the minor and cofactor of the element a31 is.
(A) 40
(B) 42
(C) 45
(D) 35
Answer
D
26. What is the derivative of xe logx ?
(A) xx (1+log x)
(B) log xe
(C) ex log x
(D) xe (1+log x)
Answer
A
27. Given a set A={1, 2, 3} and R1={(1, 1), (1, 3), (3, 1), (2, 2), (2, 1), (3, 3)}; R2={(2, 2), (1, 3), (3, 1)}; and R3={(1, 3), (3, 3)}. Which of the following relations are equivalence relation?
(A) All of them
(B) R1, R3
(C) None of them
(D) R1
Answer
C
28. If A =
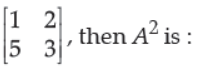

Answer
C
29. If y = e9x, then :
(A) y2 = 9e9x
(B) y2 = 81e
(C) y2 = 81e9x
(D) y2 = 81ex
Answer
C
30. The principal value of cosec−1(-2/√3) is :
(A) π/3
(B) -π/3
(C) π/2
(D) -π/2
Answer
B
31. If y = Ae8x + Be–8x, then d2y/dx2 is:
(A) 64y
(B) 8y
(C) –64y
(D) 40y
Answer
A
32. If

(A) 95/3
(B) 97/3
(C) ± √97/3
(D) ±√95/3
Answer
D
33. In which of the following, the constants of a linear function has to be maximized or minimized according to a set of given conditions
(A) Constraints
(B) Objective functions
(C) Decision variables
(D) Feasible solutions
Answer
B
34. If the curve y = –x3 + 4x2 + 8x – 32, then d2y/dx2 is
(A) –2(3x + 4)
(B) 2(3x + 4)
(C) –2(3x – 4)
(D) 2(3x – 4)
Answer
D
35. Let A =
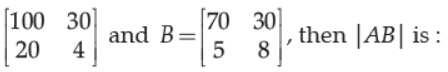
(A) 4600
(B) 5600
(C) 82000
(D) –82000
Answer
D
36. The principal value of cot−1(√3) is :
(A) π/6
(B) -π/6
(C) π/3
(D) -π/3
Answer
A
37. Let W be the set of words in the English dictionary. A relation R is defined on W as R = {(x, y) ÎW × W such that x and y have at least one letter in common}. Then R is :
(A) Symmetric but not reflexive
(B) Both Symmetric and reflexive
(C) Reflexive but not symmetric
(D) Symmetric and transitive
Answer
B
38. Let two matrices be A =[2 ] and B =

(A) 32
(B) 40
(C) 42
(D) A + B = not possible
Answer
D
39. d/dx(sin3x) at x =π/3 is:
(A) 0
(B) 1
(C) 2
(D) –3
Answer
D
40. If [x 2]

(A) 0
(B) 6
(C) –6
(D) –2
Answer
B
SECTION-C
In this section, attempt any 8 questions. Each question is of 1-mark weightage.
Questions 46-50 are based on a Case-Study.
41. The feasible region for an LPP is shown in the given Figure. Let F = 3x – 4y be the objective function.
Maximum value of F is
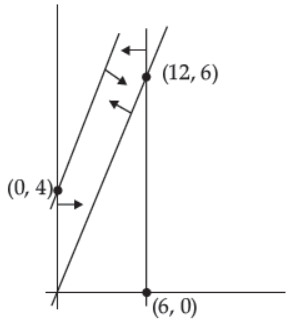
(A) 0
(B) 8
(C) 12
(D) –18
Answer
C
42. If the curve ay + x2 = 7 and x3 = y, cut orthogonally at (1, 1), then the value of a is :
(A) 1
(B) 0
(C) –6
(D) 6
Answer
D
43. If x is real, the minimum value of x2 – 8x + 17 is
(A) –1
(B) 0
(C) 1
(D) 2
Answer
C
44. Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
(A) p = 2q
(B) p = q/2
(C) p = 3q
(D) p = q
Answer
B
45. If A =

(A) λ = 2
(B) λ ≠ 2
(C) λ ≠ –2
(D) None of these
Answer
A
CASE-STUDY
Manjit wants to donate a rectangular plot of land for a school in his village. When he was asked to give dimensions of the plot, he told that if its length is decreased by 50 m and breadth is increased by 50 m, then its area will remain same, but if length is decreased by 10 m and breadth is decreased by 20 m, then its area will decrease by 5300 m2
Based on the given information, answer the following questions.
46. The equations in terms of x and y are
(A) x – y = 50, 2x – y = 550
(B) x – y = 50, 2x + y = 550
(C) x + y = 50, 2x + y = 550
(D) x + y = 50, 2x + y = 550
Answer
B
47. Which of the following matrix equation is represented by the given information

Answer
A
48. The value of x (length of rectangular field) is
(A) 150 m
(B) 400 m
(C) 200 m
(D) 320 m
Answer
C
49. The value of y (breadth of rectangular field) is
(A) 150 m
(B) 200 m
(C) 430 m
(D) 350 m
Answer
A
50. How much is the area of rectangular field?
(A) 60000 sq.m.
(B) 30000 sq.m.
(C) 30000 m
(D) 3000 m
Answer
B
