Please refer to Class 12 Mathematics Sample Paper Set N with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
1. Let [x]denote the greatest integer less than or equal to x. Then,
(a) equals p
(b) equals p + 1
(c) equals 0
(d) does not exist
Answer
D
2.

(a) not differentiable at one point
(b) not differentiable at two points
(c) differentiable at all points
(d) not continuous
Answer
A
3. If the system of linear equations
2x + 2y + 3z = a
3x – y + 5z = b
x – 3y + 2z = c
where a, b, c are non-zero real numbers, has more than one solution,then
(a) b – c – a = 0
(b) a + b + c = 0
(c) b – c + a = 0
(d) b + c – a = 0
Answer
A
4. The area (in sq units) of the region bounded by the curve x y 2 = 4 and the straight line x = 4y – 2 is
(a)7/8
(b)9/8
(c)5/4
(d)3/4
Answer
B
5.
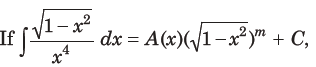
for a suitable chosen integer m and a function A(x), where C is a constant of integration, then (A(x))m equals
(a) 1/9×4
(b)-1/3x3
(c)-1/27x9
(d)1/276
Answer
C
6. The maximum value of the function
f (x) = 3x3-18x2+27x-40 on the set S = {x∈R : x2 +30 ≤ 11x}is
(a) 122
(b) – 122
(c) – 222
(d) 222
Answer
A
7. Let f : R→ R be defined by f(x)=x/1+x2, x ∈ R. Then, the range of f is
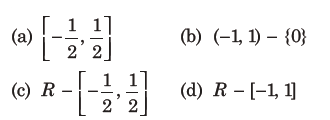
Answer
A
8. The outcome of each of 30 items was observed ; 10 items gave an outcome 1/2- d each, 10 items gave outcome 1/2 each and the remaining 10 items gave outcome1/2+d each. If the variance of this outcome data is 4/3,then|d|equals
(a)2/3
(b)5/2
(c) 2
(d) 2
Answer
C
9. Two integers are selected at random from the set { 1, 2, …… , 11}. Given that the sum of selected numbers is even, the conditional probability that both the numbers are even is
(a) 2/5
(b)1/2
(c)7/10
(d)3/5
Answer
A
10. The straight line x + 2 y = 1 meets the coordinate axes at A and B. A circle is drawn through A, B and the origin.
Then, the sum of perpendicular distances from A and B on the tangent to the circle at the origin is
(a) 2√5
(b)√5/4
(c) 4√5
(d)√5/2
Answer
D
11. The sum of the real values of x for which the middle term in the binomial expansion of

equals 5670 is
(a) 4
(b) 0
(c) 6
(d) 8
Answer
B
12. Let a1,a2,…,a10 be a GP. If a3/a1=25, then a9/a5 equals
(a) 53
(b) 2 (52)
(c) 4 (52)
(d) 54
Answer
D
13.

where x and y are real numbers, then y – x equals
(a) 91
(b) 85
(c) – 85
(d) – 91
Answer
A
14.
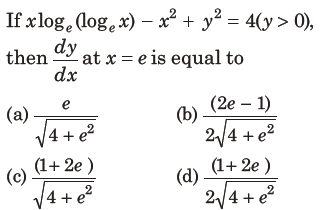
Answer
B
15. A square is inscribed in the circle x2+y2-6x+8y-103=0 with its sides parallel to the coordinate axes.
Then, the distance of the vertex of this square which is nearest to the origin is
(a) 6
(b) 13
(c) √41
(d) √137
Answer
C
16. If q is false and p∧q↔ r is true, then which one of the following statements is a tautology?
(a) p v r
(b) (p ∧ r)→(p v r)
(c) (p v r)→(p ∧ r)
(d) p ∧ r
Answer
B
17. If y(x) is the solution of the differential equation dy/dx+(2x+1/x)y=
e-2x,x>0, where y (1) =1/2e-2,then
(a) y(x) is decreasing in (1/2,1)
(b) y(x) is decreasing in (0, 1)
(c) y (loge 2) = loge 4
(d) y (loge2 ) =loge2/4
Answer
A
18. The value of r for which

is maximum, is
(a) 15
(b) 10
(c) 11
(d) 20
Answer
D
19. Two circles with equal radii are intersecting at the points (0, 1) and (0, -1). The tangent at the point (0,1) to one of the circles passes through the centre of the other circle. Then, the distance between the centres of these circles is
(a) 2
(b) 2√2
(c) 1
(d) 2
Answer
D
20. Equation of a common tangent to the parabola y 2 = 4 X and the hyperbola x y = 2 is
(a) x + 2 y + 4 = 0
(b) x – 2 y + 4 = 0
(c) 4 x + 2 y + 1 = 0
(d) x + y + 1 = 0
Answer
A
21. The value of the integral
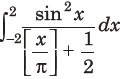
(where, [x] denotes the greatest integer less than or equal to x) is
(a) 4 – sin 4
(b) 4
(c) sin 4
(d) 0
Answer
D
22. If one real root of the quadratic equation 81x2+k x+256=0 is cube of the other root, then a value of k is
(a) 100
(b) 144
(c) -81
(d) -300
Answer
D
23. The direction ratios of normal to the plane through the points (0, – 1, 0) and (0, 0, 1) and making an angle π/4 with the plane y – z + 5 = 0 are
(a) 2, – 1, 1
(b) √2, 1, – 1
(c) 2, √2, – √2
(d) 2 √3, 1, – 1
Answer
(B.C)
24. In a triangle, the sum of lengths of two sides is x and the product of the lengths of the same two sides is y. If x2-c2=y, where c is the length of the third side of the triangle, then the circumradius of the triangle is
(a) c/3
(b) c/√3
(c) 3/2 y
(d) y/√3
Answer
B
25. The plane containing the line x -3/= y+2/-1 = z-1/3 and also containing its projection on the plane 2x + 3y – z = 5, contains which one of the following points?
(a) (-2, 2, 2)
(b) (2, 2, 0)
(c) (2, 0, – 2)
(d) (0,- 2,2)
Answer
C
26.
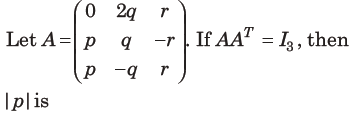
(a)1/5
(b)1/2
(c)1/3
(d)1/6
Answer
B
27. If tangents are drawn to the ellipse x2+2y2=2 at all points on the ellipse other than its four vertices,then the mid-points of the tangents intercepted between the coordinate axes lie on the curve
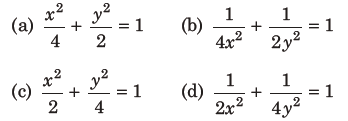
Answer
D
28. Let fk (x)=1/k (sink x+cosk x) for k = 1, 2, 3 … . Then, for all x ∈ R, the value of f4 (x)- f6(x) is equal to
(a)1/12
(b)5/12
(c)-1/12
(d)1/4
Answer
A
29. The sum of an infinite geometric series with positive terms is 3 and the sum of the cubes of its terms is 27/19. Then, the common ratio of this series is
(a)4/9
(b)2/3
(c)2/9
(d)1/3
Answer
B
30.

vectors. Then, the non-zero vector a x c is//30
Answer
A
