Students should refer to Worksheets Class 11 Mathematics Conic Sections Chapter 11 provided below with important questions and answers. These important questions with solutions for Chapter 1 Conic Sections have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Conic Sections Worksheets Class 11 Mathematics
Question: The tangents to x2+y2=a2 having inclinations α and β intersect at P. If cotα cot β = 0, then the locus of P is
(a) x +y + = 0
(b) x -y − = 0
(c) xy = 0
(d) None of these
Answer
C
Question: The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3) is
(a) 10/3
(b) 3/5
(c) 6/5
(d) 5/3
Answer
A
Question: The two circles x2+y2=ax and x2+y2=c2, (c>0) touch each other if
(a) |a| =c
(b) a =c
(c) |a| =2c
(d) 2|a| =c
Answer
A
Question: The equation of the circle passing through the points ( 1,0 ) and (0, 1) and having the smallest radius is
(a) x2+y2+x+y-2=0
(b) x2+y2-2x-2y-1=0
(c) x2+y2-x-y=0
(d) x2+y2+2x+2y-7=0
Answer
C
Question: The circle passing through (1, −2) and touching the axis to x at (3, 0) also passes through the point
(a) (−5 2,)
(b) (2,-5)
(c) (5,-2)
(d) (-2,5)
Answer
C
Question: The circle x2+y2=4x+8y+5 intersects the line 3x-4y=m at two distinct points, if
(a) −85<m<-35
(b) -35<m<15
(c) 15 <m<65
(d) 35 <m<85
Answer
B
Question: The point diameterically opposite to the point P (1, 0) on the circle x2+y2+2x+4y-3=0 is
(a) (3, 4)
(b) (3, − 4)
(c) (− 3, 4)
(d) (− 3, − 4)
Answer
D
Question: Consider a family of circles which are passing through the point (−1, 1) and are tangent to x-axis. If (h ,k ) is the centre of circle, then
(a) k ≥ 1/2
(b) − 1/2 ≤ k ≤1/2
c) k ≤ 1/2
(d) 0 < k<1/2
Answer
A
Question: If P and Q are the points of intersection of the circles x2+y2+3x+7y+2p-5=0 and x2=y2+2x+2y-p2=0, then there is a circle passing through P, Q and (1, 1) and
(a) all values of p
(b) all except one value of p
(c) all except two values of p
(d) exactly one value of p
Answer
C
Question: Any chord of the circle x2+y2=25 subtends a right angle at the centre. Then, the locus of the centroid of the triangle made by the chord and a moving point P on the circle is
(a) parabola
(b) circle
(c) rectangular hyperbola
(d) ellipse
Answer
B
P is a variable point on the line L = 0.Tangents are drawn to the circle x2+y2=4from P to touch it at Q and R. The parallelogram PQSR is completed.
Question: If P ≡ ( 2,3), then the centre of circumcircle of ∆ QRS is
(a) (2/13,7/26)
(b) (2/13,3/26)
(c) (3/13,9/26)
(d) (3/13,2/13)
Answer
C
Question: If L≡ 2x+ y= 6, then the locus of circumcentre of ∆PQR is
(a) 2x-y=4
(b) 2x+y=3
(c) x -2y=4
(d) x+2y =3
Answer
B
Question: The equation x2+ y2+2gx+2fy+c=0 will represent a real circle, if
(a) g2+f2-c<0
(b) g2+f2-c≥0
(c) always
(d) None of these
Answer
B
Question: The equation of circle which touches the axes of coordinates and the line x/3+ y/3 4 + = 1 and whose centre lies in the first quadrant is x2+y2-2cx-2cy+c2=o, where c is
(a) 1
(b) 2
(c) 3
(d) None of these
Answer
A
Question: If the points (2, 0), (0, 1), (4, 5) and (0, c) are concyclic, then the value of c is
(a) 1
(b) 14/3
(c) 5
(d) None of these
Answer
B
Question: The tangent to x2+y2 =9 which is parallel to y-axis and does not lie in the third quadrant touches the circle at the point
(a) (3, 0)
(b) (–3, 0)
(c) (0, 3)
(d) (0, –3)
Answer
A
Question: The coordinates of the middle point of the chord cut off 2x-5y+18=0 by the circle x2+y2-6x+2y-54=0are
(a) (1, 4)
(b) (2, 4)
(c) (4, 1)
(d) (1, 1)
Answer
A
Question: Equation of the circle with centre on the y-axis and passing through the origin and (2, 3) is
(a) x2+y2+13y=0
(b) 3x2+3y2-13y=0
(c) x2+y2+13x+3=0
(d) 6x2+6y2-13x=0
Answer
B
Question: Polar of origin (0, 0) with respect to the circle
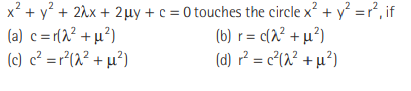
Answer
C
Question: Tangents drawn from the point (4, 3) to the circle x2+y2-2x-4y=0 are inclined at an angle
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
D
Question: The tangents drawn from the origin to the circle x2+y2-2rx-2hy+h2=0 are perpendicular, if
(a) h = r
(b) h =-r
(c) r2=h2
(d) All of these
Answer
D
Question: The equation of the unit circle concentric with x2+y2-8x+4y-8=0 is
(a) x2+y2- 8x +4y -8=0
(b) x2+ y2-8x +4y+8=0
(c) x2+y2– 8x+ 4y -28 =0
(d) x2+ y2-8x+4y+19=0
Answer
D
Question: The locus of the centre of a circle which touches externally the circle x2+y2-6y+14=0 and also touches the y-axis is given by the equation
(a) x2 -6x -10y +14=0
(b) x2– 10x -6y +14=0
(c) y2 -6x -10y +14=0
(d) y2 -10x -6y +14=0
Answer
D
Question: If a circle passes through the point (1, 2) and cuts the circle x2+y2=4 orthogonally, then the equation of the locus of its centre is
(a) x2+y2-3x-8y+1=0
(b) x2+y2-2x-6y-7=0
(c) 2x+4y-9=0
(d) 2x+4y-1=0
Answer
C
Question: The number of common tangents to the circles x2+y2+2x+8y-23=0 and x2+y2-4x-10y+19=0 are
(a) 4
(b) 2
(c) 3
(d) 1
Answer
C
Question: If the radical axis of the circles x2+y2+2gx+2fy+c and 2x2+2y2+3x+8y+2c=0 touches the circle x2+y2+2x+2y+1=0, then
(a) g = 3/4 and ≠2
(b) g ≠ 3/4 and f=2
(c) g = 3/4 or f = 2
(d) None of these
Answer
C
Question: If the circle x2+y2+2gx+2fy+c=0 bisects the circumference

Answer
B
Question: The common chord of x2+y2-4x-4y=0 and x2+y2=16 subtends at the origin an angle equal to
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
D
Question: The radical axis of the co axial system of circles with limiting point (1,2) and (–2, 1) is
(a) x + = 3y=0
(b) 3x+y=0
(c) 2x+3y=0
Answer
B
Question: The circles whose equations are x2+y2+c2=2x and x2+y2+c2=2by will touch one another externally, if
(a) 1/b2+1/c2=1/a2
(b) 1/c2+1/a2=1/b2
(c) /a2+1/b2=1/c2
(d) None of these
Answer
C
Question: Find the equation of circle with centre (-a,-b, ) and radius √a2-b2.
(a) x2+ y2 -2ax-2by-2b2=0
(b) x2+y2+2ax+by+2b2=0
(c) x2+y2+2ax+2by+2b2=0 y
(d) None of the above
Answer
C
Question: The centre of a circle is (2, – 3) and the circumference is 10π. Then, the equation of the circle is
(a) x2 +y2+ 4x+ 6y+ 12=0
(b) x2 +y2– 4x+ 6y+12=0
(c) x2+ y2– 4x+ 6y- 12=0
(d) x2+ y2 – 4x- 6y- 12=0
Answer
C
Question: If one end of a diameter of the circle x2+y2-4x-6y+11=0 is (3, 4), then find the coordinate of the other end of the diameter.
(a) (2, 1)
(b) (1, 2)
(c) (1, 1)
(d) None of these
Answer
B
Question: Equation of a circle which passes through (3, 6) and touches the axes is
(a) x2+ y2+ 6x+ 6y+ 3=0
(b) x2+ y2– 6x- 6y- 9=0
(c) x2+ y2– 6x- 6y+ 9=0
(d) None of the above
Answer
C
Question: Circle x2+y2-2x- λx-1=0 passes through two fixed points, coordinates of the points are
(a) (0, ±1)
(b) (± 1,0 )
(c) (0, 1) and (0, 2)
(d) (0,1) and (0,-2 )
Answer
A
Question: Equation of the circle with centre on the y-axis and passing through the origin and the point (2, 3) is
(a) x2+ y2+13y=0
(b) 3x2+ 3y2+13x+3=0
(c) 6x2+ 6y2-26y=0 6
(d) x2+ y2+13x+3=0
Answer
C
Question: The circle x2+y2-8x+4y+4=0 touches
(a) x-axis
(b) y-axis
(c) both axis
(d) neither x-axis nor y-axis
Answer
B
Question: If the lines 2x-3y=5 and 3x-4y=7 are the diameters of a circle of area 154 sq units, then find the equation of the circle.
(a) x2 + y2 – 2x +2y =40
(b) x2 + y2 – 2x- 2y =47
(c) x2 + y2 – 2x +2y =47
(d) None of the above
Answer
C
Question: Find the equation of the circle which touches the both axes in first quadrant and whose radius is a.
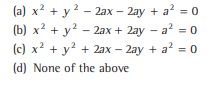
Answer
A
Question: If 2(x2+y2)+4λx+λ2=0 represents a circle of meaningful radius, then the range of real values of λ is
(a) R
(b) (0, 0 + ∞)
(c) (- ∞, 0)
(d) None of these
Answer
A
Question: The equation of the circle on the common chord of the circles (x-a)2 +y2 = a2) and x2+ (y+b)2 =b2 as diameter, is

Answer
C
Question: The equation of the circle passing through (1, 1) and the points of intersection of x2+y2+13x-3y=0 and 2x2+2y2+4x-7y-25=0 is
(a) 4x2+ 4y2– 30x -10y= 25=0
(b) 4x2+ 4y2 +30x -13y- 25=0
(c) 4x2+4y2– 17x -10y+ 25=0
(d) None of the above
Answer
B
Question: Find the equation of a circle concentric with the circle x2+y2-6x+12y-15=0 and has double of its area.
(a) x2+ y2– 6x+12y -15=0
(b)x2+ y2– 6x-12y +15=0
(c) x2+ y2– 6x+12y +15=0
(d) None of the above
Answer
A
Question: If the circle x2+y2+4x+22y+c=0 bisects the circumference of the circle x2+y2-2x+8y-d=0, then c +d is equal to
(a) 60
(b) 50
(c) 40
(d) 30
Answer
B
Question: If (− 3 2, ) lies on the circle x2+y2+2gx+2fy+0=0 which is concentric with the circle x2+y2+6x+8y-5=0, 8 5 0, then c is equal to
(a) 11
(b) − 11
(c) 24
(d) 100
Answer
B
Question: Two circles with centres (2, 3) and (5, 6) cut orthogonally. If radius of both circles are equal, then radius is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question: The equation of the circle which passes through the
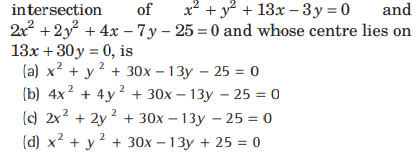
Answer
B
Question: If P is a point such that the ratio of the squares of the
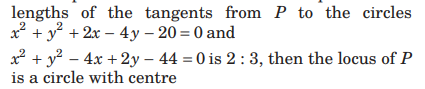
(a) (7,-8)
(b) (-7,8)
(c) (7,8)
(d) (-7,-8)
Answer
B
Question: Equation of the circle passing through the point (3,4) and concentric with the circle x2+y2-2x-4y+1=0 is
(a) x2+ y2 – 2x -4y =0
(b) x2+ y2 -2x -4y+3 =0
(c) x2+ y2 -2x -4y+3 =0
(d) None of the above
Answer
C
Question: Tangents drawn from the point P( 1, 8) to the circle x2+ y2-6x-11=0 touch the circle at the points A and B. The equation of the circumcircle of the ∆ PAB is
(a) x2 +y2 + 4x – 6y + 19=0
(b) x2 +y2 – 4x – 10y +19=0
(c) x2 +y2-2x + 6y – 29=0
(d) x2 +y2– 6x- 4y+ 19=0
Answer
B
Question: The locus of the centre of a circle which cuts orthogonally the circle x2+y2-20x+4=0 and which touches x = 2 , is
(a) y2=16x+4
(b) x2=16y
(c) x2=16y+4
(d) y2=16x
Answer
D
Question: If two circles, each of radius 5 units, touch each other at (1, 2) and the equation of their common tangent is 4x+3y=10, then equation of the circle a portion of which lies in all the quadrants, is
(a) x2+ y2-1 0x-10y +25 =0
(b) x2+ y2+ 6x+2y -15 =0
(c) x2 + y2+ 2x+ 6y-15 =0
(d) x2 +y2 +10x +10y +25= 0
Answer
B
Question: The circle x2+y2-10x-14y+24=0 cuts an intercepts on y-axis of length
(a) 5
(b) 10
(c) 1
(d) None of these
Answer
B
Question: The length of the transversal common tangent to the circle x2+ y2=1 and (x-t)2+ y2=1 is √21, then t is equal to
(a) ± 2
(b) ± 5
(c) ± 3
(d) None of these
Answer
B
Question: C1 and C2 are circles of unit radius with centres at (0,0) and (1,0) respectively. C3 is a circle of unit radius, passes through the centres of the circles C1 and C2 1and have its centre above x-axis. Equation of the common tangent to C1 and C2 which does not pass through C2, is
(a) x- √3y +2=0
(b) √3x- y+2=0
(c) √3x -y- 2=2
(d) x+ √3y+ 2=0
Answer
B
Question: The locus of centre of family of circle passing through the origin and cutting the circle x2+y2+4x- 6y-13=0 rthogonally, is
(a) 4x+6y+13=0
(b) 4x-6y+ 13=0
(c) 4x+6y- 13=0
(d) 4x-6y-1 3=0
Answer
D
Question: The locus of centre of a circle x2+y2-2x-2y+1=0, which rolls outside the circle x2+y2-6x+8y=0,y x y 2 2 + − + = 6 is
(a) x2 +y2– 2x- 2y -34 =0
(b) x2 +y2-6x – 8y +11=0
(c) x2 +y2-6x +8y -11=0
(d) None of the above
Answer
C
Question: The centre of the circle, which cuts orthogonally each of the three circles x2 +y2 + 2x+ 17y + 4=0 and x2+y2+7x+6y+11=0,x2+y2– x+ 22y +3=0, is
(a) (3,2)
(b) (1,2)
(c) (2,3)
(d) (0,2)
Answer
A
Assertion and Reason
Each of these questions contains two statements : Statement I (Assertion) and Statement II (Reason). Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select one of the codes (a), (b), (c) and (d) given below.
(a) Statement I is true, Statement II is true; Statement II is a correct explanation for Statement I.
(b) Statement I is true, Statement II is true; Statement II is not a correct explanation for Statement I.
(c) Statement I is true; Statement II is false.
(d) Statement I is false; Statement II is true.
Question: Let C1 and be two circles with C2 lying inside C1.
Statement I A circle C lying inside C1 touches C1 internally and C2 externally. Then, the locus of the centre of C is an ellipse.
Statement II If A B and are foci and P be any point on the ellipse, then AP+ BP = constant.
Answer
A
Question: Statement I Circle x2+y2-6x-4y+9=0 9 0 bisects the circumference of the circle x2+y2-8x-6y-23=0.
Statement II Centre of first circle lie on the second circle.
Answer
B
Question: Statement I A ray of light incident at the point (–3, –1) gets reflected from the tangent at (0, –1) to the circle x2+y2=1. If the reflected ray touches the circle, then equation of the reflected ray is 4y-3x=5.
Statement II The angle of incidence = angle of reflection i.e., ∠i = ∠r
Answer
B
Question: Statement I Number of circles passing through ( -2,1), (-1,0), (-4,3) is 1.
Statement II Through three non-collinear points in a plane only one circle can be drawn.
Answer
D
Question: Consider L1:2x+3y+p-3=0 and L2:2x+3y+p+3=0, where p is a real number and C:x2+y2+6x-10y+30=0
Statement I If line L1 is a chord of circle C, then L2 is not always a diameter of circle C.
Statement II If line L1 is a diameter of circle C, then L2 is not a chord of circle C .
Answer
C
Question: Statement I Circles x2+y2=4 and x2+y2-8x+7=0 intersect each other at two distinct points.
Statement II Circles with centres C1 and C2 and radii r1 and r2 intersect at two distinct points, if |C1C2| <r1+r2.
Answer
C
Question: Consider two circles S ≡x2+y2+2gx+2fy=0 and S’≡ x2+y2+2g’x+2f’y=0
Statement I If two circles S S and ′ touch each other, then f ‘g= fg ′ .
Statement II Two circles touch each other, if line joining their centres is perpendicular to all possible common tangents.
Answer
B

