VBQs Permutations and Combinations Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Permutations and Combinations Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Permutations and Combinations VBQs Class 11 Mathematics
Question. Number of ways in which 20 different pearls of two colours can be set alternately on a necklace, there being 10 pearls of each colour.
(a) 6 × (9!)2
(b) 12!
(c) 4 × (8!)2
(d) 5 × (9!)2
Answer
D
Question. If the letters of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number
(a) 601
(b) 600
(c) 603
(d) 602
Answer
A
Question. If the letters of the word RACHIT are arranged in all possible ways as listed in dictionary. Then, what is the rank of the word RACHIT?
(a) 479
(b) 480
(c) 481
(d) 482
Answer
C
Question. If 1/6! + 1/7! = x/8! , then the value of x = 2m. The value of m is
(a) 2
(b) 4
(c) 6
(d) 5
Answer
D
Question. Total number of eight digit numbers in which all digits are different is
(a) 8.7!/3
(b) 5.8!/3
(c) 8.9!/2
(d) 9.9!/2
Answer
D
Question. In how many ways 3 mathematics books, 4 history books, 3 chemistry books and 2 biology books can be arranged on a shelf so that all books of the same subjects are together?
(a) 41472
(b) 41470
(c) 41400
(d) 41274
Answer
A
Question. If nCr denotes the number of combination of n things taken r at a time, then the expression nCr+1 + nCr–1 + 2 × nCr equals
(a)n+1Cr+1
(b) n+2Cr
(c) n+2Cr+1
(d) n+1Cr
Answer
C
Question. Four writers must write a book containing 17 chapters. The first and third writer must write 5 chapters each, the second writer must write 4 chapters and fourth writer must write three chapters. The number of ways that can be found to divide the book between four writers, is
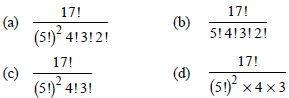
Answer
C
Question. Four couples (husband and wife) decide to form a committee of four members, then the number of different committees that can be formed in which no couple finds a place is
(a) 15
(b) 16
(c) 20
(d) 21
Answer
B
Question. The number of 3 digit numbers having at least one of their digit as 5 are
(a) 250
(b) 251
(c) 252
(d) 253
Answer
C
Question. How many different words can be formed by jumbling the letters in the word MISSISSIPPI in which no two S are adjacent?
(a) 8. 6C4. 7C4
(b) 6.7. 8C4
(c) 6. 8. 7C4.
(d) 7. 6C4. 8C4
Answer
D
Question. The number of parallelograms that can be formed from a set of four parallel lines intersecting another set of three parallel lines is
(a) 6
(b) 18
(c) 12
(d) 9
Answer
B
Question. Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If Tn + 1 − Tn = 21, then n equals`
(a) 5
(b) 7
(c) 6
(d) 4
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 1 4 3 2
(b) 1 3 4 2
(c) 2 4 3 1
(d) 2 3 4 1
Answer
A
Question. In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.
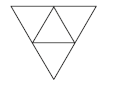
(a) 20
(b) 24
(c) 28
(d) 30
Answer
B
Question. Number of words from the letters of the words BHARAT in which B and H will never come together is
(a) 210
(b) 240
(c) 422
(d) 400
Answer
B
Question. If n + 2C8 : n – 2P4 = 57 : 16, then the value of n is:
(a) 20
(b) 19
(c) 18
(d) 17
Answer
B
Question. A father with 8 children takes them 3 at a time to the zoological garden, as often as he can without taking the same 3 children together more than once. The number of times he will go to the garden is
(a) 56
(b) 100
(c) 112
(d) None of these
Answer
A
Question. The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is
(a) 72
(b) 96
(c) 90
(d) 98
Answer
C
Question. If nC9 = nC8, what is the value of nC17 ?
(a) 1
(b) 0
(c) 3
(d) 17
Answer
A
Question . The sum of the digits in the unit place of all the numbers formed with the help of 3, 4, 5, 6 taken all at a time is
(a) 432
(b) 108
(c) 36
(d) 18
Answer
B
Question. The number of ways in which we can choose a committee from four men and six women so that the committee include at least two men and exactly twice as many women as men is
(a) 94
(b) 126
(c) 128
(d) None of these
Answer
A
Question. Using the digits 1, 2, 3, 4, 5, 6, 7, a number of 4 different digits is formed. Find :

Match the questions in column-I with column-II and choose the correct option from the codes given below.
Codes:
A B C D
(a) 1 2 3 4
(b) 3 1 4 2
(c) 1 3 4 2
(d) 4 2 3 1
Answer
C
Question. Determine n if 2nC3 : nC2 = 12 : 1
(a) 5
(b) 3
(c) 4
(d) 1
Answer
A
Question. In a small village, there are 87 families, of which 52 families have at most 2 children. In a rural development programme 20 families are to be chosen for assistance, of which at least 18 families must have at most 2 children. In how many ways can the choice be made?
(a) 52C18 35C2
(b) 52C18× 35C2+ 52C19× 35C1+ 52C20
(c) 52C18+ 35C2+ 52C19
(d) 52C18× 35C2+ 35C1× 52C19
Answer
B
Question. Value of n!/(n− r)! when n = 6, r = 2 is 5 m. The value of m is
(a) 2
(b) 4
(c) 6
(d) 5
Answer
C
Question. The number of ways of distributing 50 identical things among 8 persons in such a way that three of them get 8 things each, two of them get 7 things each, and remaining 3 get 4 things each, is equal to
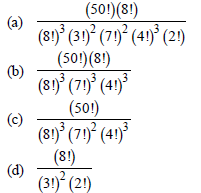
Answer
D
Question. Total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to
(a) 60
(b) 120
(c) 7200
(d) 720
Answer
C
Question. For a game in which two partners play against two other partners, six persons are available. If every possible pair must play with every other possible pair, then the total number of games played is
(a) 90
(b) 45
(c) 30
(d) 60
Answer
B
Question. If 30Cr + 2 = 30Cr – 2, then r equals:
(a) 8
(b) 15
(c) 30
(d) 32
Answer
B
Question. Find n if n – 1P3 : nP4= 1 : 9
(a) 2
(b) 6
(c) 8
(d) 9
Answer
D
Question. Eighteen guests are to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on the other side of the table. The number of ways in which the seating arrangement can be done equals
(a) 11C4 (9!)2
(b) 11C6 (9!)2
(c) 6P0 × 5P0
(d) None of these
Answer
B
STATEMENT TYPE QUESTIONS
Question. Consider the following statements.
I. If there are n different objects, then nCr = nCn−r 0 ≤ r ≤ n.
II. If there are n different objects, then nCr + nCr– 1 = n+1Cr, 0 ≤ r ≤ n
Choose the correct option.
(a) Both are false.
(b) Both are true.
(c) Only I is true.
(d) Only II is true.
Answer
B
Question. Consider the following statements.
I. If nPr = nPr+1 and nCr = nCr–1, then the values of n and r are 3 and 2 respectively.
II. From a class of 32 students, 4 are to be chosen for a competition. This can be done in 32C2 ways.
Choose the correct option.
(a) Only I is true.
(b) Only II is true.
(c) Both are false.
(d) Both are true.
Answer
A
Question. The number of 4 letter words that can be formed from letters of the word ‘PART’, when:
Statement I : Repetition is not allowed is 24.
Statement II : Repetition is allowed is 256.
Which of the above statement(s) is/are true?
(a) Only I
(b) Only II
(c) Both I and II
(d) Neither I nor II
Answer
C
Question. Consider the following statements.
I. If n is an even natural number, then the greatest among nC0, nC1 , nC2, …, nCn is nCn/2.
II. If n is an odd natural number, then the greatest among nC0, nC1 , nC2, …, nCn is nCn−1/2 or nCn+ 1/2.
Choose the correct option.
(a) Only I is false.
(b) Only II is true.
(c) Both are true.
(d) Both are false.
Answer
C