VBQs Straight Lines Class 11 Mathematics

VBQs Straight Lines Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Straight Lines Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.

Straight Lines VBQs Class 11 Mathematics

Question. The points A(1, 3) and C(5, 1) are the opposite vertices of rectangle. The equation of line passing through other two vertices and of gradient 2, is
(a) 2x + y – 8 = 0
(b) 2x – y – 4 = 0
(c) 2x – y + 4 = 0
(d) 2x + y + 7 = 0

Question. If a line with slope m makes x-intercept d. Then equation of the line is :
(a) y = m(d – x)
(b) y = m(x – d)
(c) y = m(x + d)
(d) y = mx + d

Question. The relation between a, b, a’ and b’ such that the two lines ax + by = c and a’x + b’y = c’ are perpendicular is
(a) aa’ – bb’ = 0
(b) aa’ + bb’ = 0
(c) ab + a’b’ = 0
(d) ab – a’b’ = 0

Question. The straight lines x + 2y – 9 = 0, 3x + 5y – 5 = 0 and ax + by = 1 are concurrent if the straight line 35x – 22y + 1 = 0 passes through :
(a) (a, b)
(b) (b, a)
(c) (a, – b)
(d) (– a, b)

Question. The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the value of m + c. 
(a) 2
(b) 3
(c) 4
(d) 5

Question. If the mid-point of the section of a straight line intercepted between the axes is (1, 1), then what is the equation of this line?
(a) 2x + y = 3
(b) 2x – y = 1
(c) x – y = 0
(d) x + y = 2

Question. If (– 4, 5) is one vertex and 7x – y + 8 = 0 is one diagonal of a square, then the equation of second diagonal is
(a) x + 3y = 21
(b) 2x – 3y = 7
(c) x + 7y = 31
(d) 2x + 3y = 21

Question. Choose the correct statement which describe the position of the point (–6, 2) relative to straight lines 2x + 3y – 4 = 0 and 6x + 9y + 8 = 0.
(a) Below both the lines
(b) Above both the lines
(c) In between the lines
(d) None of these

Question. Value of x so that 2 is the slope of the line through (2, 5) and (x, 3) is
(a) 0
(b) 1
(c) 2
(d) 3

Question. The equation of a straight line passing through (–3, 2) and cutting an intercept equal in magnitude but opposite in sign from the axes is given by
(a) x – y + 5 = 0
(b) x + y – 5 = 0
(c) x – y – 5 = 0
(d) x + y + 5 = 0

Question. A line passes through P (1, 2) such that its intercept between the axes is bisected at P. The equation of the line is
(a) x + 2y = 5
(b) x – y + 1 = 0
(c) x + y – 3 = 0
(d) 2x + y – 4 = 0

Question. If the area of the triangle with vertices (x, 0), (1, 1) and (0, 2) is 4 square unit, then the value of x is :
(a) – 2
(b) – 4
(c) – 6
(d) 8

Question. A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). The co-ordinates of the point A is
(a) (13/5 , 0)
(b) (5/13 , 0)
(c) (–7, 0)
(d) None of these

Question. If p be the length of the perpendicular from the origin on the straight line x + 2by = 2p ,then what is the value of b?
(a) 1/p
(b) p
(c) 1/2
(d) √3/2

Question. The vertices of a triangle ABC are (1, 1), (4, – 2) and (5, 5) respectively. Then equation of perpendicular dropped from C to the internal bisector of angle A is
(a) y – 5 = 0
(b) x – 5 = 0
(c) 2x + 3y –7 = 0
(d) None of these

Question. The distance between the lines 3x + 4y = 9 and 6x + 8y = 15 is:
(a) 3/2
(b) 3/10
(c) 6
(d) 9/4

Question. The line parallel to the x-axis and passing through the intersection of the lines ax + 2by + 3b = 0 and bx – 2ay – 3a = 0, where (a, b) ≠ (0, 0) is
(a) Above the x-axis at a distance of 3/2 from it
(b) Above the x-axis at a distance of 2/3 from it
(c) Below the x-axis at a distance of 3/2 from it
(d) Below the x-axis at a distance of 2/3 from it

Question. Reduce the equation √3x + y−8 =0 into normal form. The value of p is
(a) 2
(b) 3
(c) 4
(d) 5

Question. The lines a₁x + b₁y + c₁= 0 and a₂x + b₂y + c₂ = 0 are perpendicular to each other
(a) a₁b₁ – b₁a₂ = 0
(b) a₁²b₂ + b₁²a₂ = 0
(c) a₁b₁ + a₂b₂ = 0
(d) a₁b₂ + b₁b₂ = 0

Question. The point (x, y) lies on the line with slope m and through the fixed point (x₀, y₀) if and only if its coordinates satisfy the equation y – y₀ is equal to ……… .
(a) m(x – x₀)
(b) m(y – x₀)
(c) m(y – x)
(d) m(x – y₀)

Question. The reflection of the point (4, – 13) in the line 5x + y + 6 = 0 is
(a) (–1, –14)
(b) (3, 4)
(c) (0, 0)
(d) (1, 2)

Question. The inclination of the line x – y + 3 = 0 with the positive direction of x-axis is
(a) 45°
(b) 135°
(c) –45°
(d) –135°

Question. Let the perpendiculars from any point on the line 7x + 56y = 0 upon 3x + 4y = 0 and 5x – 12y = 0 be p and p’, then
(a) 2p = p’
(b) p = 2p’
(c) p = p’
(d) None of these

Question. The lines p(p² +1) x – y + q = 0 and (p² + 1)²x + (p² + 1) y + 2q = 0 are perpendicular to a common line for
(a) exactly one value of p
(b) exactly two values of p
(c) more than two values of p
(d) no value of p

STATEMENT TYPE QUESTIONS 

Question. Slope of the lines passing through the points
I. (3, – 2) and (– 1, 4) is −3/2
II. (3, – 2) and (7, – 2) is 0.
III. (3, – 2) and (3, 4) is 1.
Choose the correct option.
(a) Only I and III are true
(b) Only I and II are true
(c) Only II and III are true
(d) None of these

Question. The distances of the point (1, 2, 3) from the coordinate axes are A, B and C respectively. Now consider the following equations:
I. A² = B² + C²
II. B² = 2C²
III. 2A²C² = 13 B²
Which of these hold(s) true?
(a) Only I
(b) I and III
(c) I and II
(d) II and III

Question. Equation of a line is 3x – 4y + 10 = 0
I. Slope of the given line is 3/4.
II. x-intercept of the given line is −10/3.
III. y-intercept of the given line is 5/2.
Choose the correct option.
(a) Only I and II are true
(b) Only II and III are true
(c) Only I and III are true
(d) All I, II and III are true

Question. Consider the following statements.
I. The distance between two points (x₁, y₁) and (x₂, y₂) is given by

II. The coordinates of the mid-point of the line segment joining the points (x₁, y₁) and (x₂, y₂)

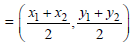
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false

Question. Consider the following statements.
I. If (a, b), (c, d) and (a – c, b – d) are collinear, then bc – ad = 0
II. If the points A (1, 2), B (2, 4) and C (3, a) are collinear, then the length BC = 5 unit.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false

Question. Consider the following statements.
The three given points A, B, C are collinear i.e., lie on the same straight line, if
I. area of ΔABC is zero.
II. slope of AB = Slope of BC.
III. any one of the three points lie on the straight line joining the other two points.
Choose the correct option
(a) Only I is true
(b) Only II is true
(c) Only III is true
(d) All are true

Question. Consider the following statements.
I. Let A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) be the vertices of a triangle then centroid is
(x₁ + x₂ + x₃/3, y₁ + y₂ + y₃/3)
II. If the point P(x , y) divides the line joining the points A(x₁, y₁) and B(x₂, y₂) in the ratio m : n (internally), then
x = mx₂ + nx₁/m + n , y = my₂ + ny₁/m + n
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false

Question. Consider the following statements about straight lines :
I. Slope of horizontal line is zero and slope of vertical line is undefined.
II. Two lines are parallel if and only if their slopes are equal.
III. Two lines are perpendicular if and only if product of their slope is – 1.
Which of the above statements are true ?
(a) Only I
(b) Only II
(c) Only III
(d) All the above

Question. A rectangle is inscribed in a circle with a diameter lying along the line 3y = x + 7. If the two ad acent vertices of the rectangle are (–8, 5) and (6, 5), then the area of the rectangle (in sq. units) is:
(a) 84
(b) 98
(c) 72
(d) 56

Question. Two sides of a parallelogram are along the lines, x + y = 3 and x – y + 3 = 0. If its diagonals intersect at (2, 4), then one of its vertex is:
(a) (3, 5)
(b) (2, 1)
(c) (2, 6)
(d) (3, 6)

Question. Consider the set of all lines px + qy + r = 0 such that 3p + 2q + 4r = 0. Which one of the following statements is true?
(a) The lines are concurrent at the point (3/4, 1/2)
(b) Each line passes through the origin.
(c) The lines are all parallel.
(d) The lines are not concurrent.

Question. Let the equations of two sides of a triangle be 3x – 2y + 6 = 0 and 4x + 5y – 20 = 0. If the orthocentre of this triangle is at (1, 1), then the equation of its third side is:
(a) 122y – 26x – 1675 = 0
(b) 122y + 26x + 1675 = 0
(c) 26x + 61y + 1675 = 0
(d) 26x – 122y – 1675 = 0

Question. The foot of the perpendicular drawn from the origin, on the line, 3x + y = l(l ¹ 0) is P. If the line meets x-axis at A and y-axis at B, then the ratio BP : PA is
(a) 9 : 1
(b) 1 : 3
(c) 1 : 9
(d) 3 : 1

Question. The sides of a rhombus ABCD are parallel to the lines, x – y + 2 = 0 and 7x – y + 3 = 0. If the diagonals of the rhombus intersect at P(1, 2) and the vertex A (different from the origin) is on the y-axis, then the ordinate of A is
(a) 2
(b) 7/4
(c) 7/2
(d) 5/2

Question. Let a, b, c and d be non- ero numbers. If the point of intersection of the lines 4ax + 2ay + c = 0 and 5bx + 2by + d = 0 lies in the fourth quadrant and is equidistant from the two axes then
(a) 3bc – 2ad = 0
(b) 3bc + 2ad = 0
(c) 2bc – 3ad = 0
(d) 2bc + 3ad = 0

Question. If the three distinct lines x + 2ay + a = 0, x + 3by + b = 0 and x + 4ay + a = 0 are concurrent, then the point (a, b) lies on a:
(a) circle
(b) hyperbola
(c) straight line
(d) parabola

Question. The base of an equilateral triangle is along the line given by 3x + 4y = 9. If a vertex of the triangle is (1, 2), then the length of a side of the triangle is:
(a) 2√3/15
(b) 4√3/15
(c) 4√3/5
(d) 2√3/5

Question. If the extremities of the base of an isosceles triangle are the points (2a, 0) and (0, a) and the equation of one of the sides is x = 2a, then the area of the triangle, in square units, is :
(a) (5/4)a²
(b) (5/2)a²
(c) 25a²/4
(d) 5a²

Question. If the x-intercept of some line L is double as that of the line, 3x + 4y = 12 and the y-intercept of L is half as that of the same line, then the slope of L is :
(a) – 3
(b) – 3/8
(c) – 3/2
(d) – 3/16

Question. If the image of point P(2, 3) in a line L is Q(4, 5), then the image of point R(0, 0) in the same line is:
(a) (2, 2)
(b) (4, 5)
(c) (3, 4)
(d) (7, 7)

Question. A straight line through the point A (3, 4) is such that its intercept between the axes is bisected at A. Its equation is
(a) x + y = 7
(b) 3x – 4y + 7 = 0
(c) 4x + 3y = 24
(d) 3x + 4y = 25

Question. Let θ₁ be the angle between two lines 2x + 3y + c₁ = 0 and – x + 5y + c₂ = 0 and θ₂ be the angle between two lines 2x + 3y + c₁ = 0 and – x + 5y + c₃ = 0, where c₁, c₂, c₃ are any real numbers :
Statement-1: If c₂ and c₃ are proportional, then θ₁ = θ₂.
Statement-2: θ₁ = θ₂ for all c₂ and c₃.
(a) Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation of Statement-1.
(b) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation of Statement-1.
(c) Statement-1 is false; Statement-2 is true.
(d) Statement-1 is true; Statement-2 is false.

Question. Locus of mid point of the portion between the axes of x cosα + y sinα = p whre p is constant is
(a) x² + y² = 4/p²
(b) x² + y² = 4p²
(c) 1/x² + 1/y² = 2/p²
(d) 1/x² + 1/y² = 4/p²

Question. Let L denote the line in the xy-plane with x and y intercepts as 3 and 1 respectively. Then the image of the point (–1, – 4) in this line is:
(a) (11/5, 28/5)
(b) (29/5, 8/5)
(c) (8/5, 29/5)
(d) (29/5, 11/5)

Question. If the three lines x – 3y = p, ax + 2y = q and ax + y = r form a right-angled triangle then :
(a) a² – 9a + 18 = 0
(b) a² – 6a – 12 = 0
(c) a² – 6a – 18 = 0
(d) a² – 9a + 12 = 0

Question. Consider the straight lines
L₁ : x – y = 1
L₂ : x + y = 1
L₃ : 2x + 2y = 5
L₄ : 2x – 2y = 7
The correct statement is
(a) L₁ || L₄ , L₂ || L₃ , L₁ intersect L₄.
(a) L₁ ⊥ L₂ , L₁ || L₃ , L₁ intersect L₂.
(a) L₁ ⊥ L₂ , L₂ || L₃ , L₁ intersect L₄.
(a) L₁ ⊥ L₂ , L₁ ⊥ L₃ , L₂ intersect L₄.

Question. If a, b, c ∈ R and 1 is a root of equation ax² + bx + c = 0, then the curve y = 4ax² + 3bx + 2c, a ≠ 0 intersect x-axis at
(a) two distinct points whose coordinates are always rational numbers
(b) no point
(c) exactly two distinct points
(d) exactly one point

Question. Let L be the line y = 2x, in the two dimensional plane.
Statement 1: The image of the point (0, 1) in L is the point (4/5, 3/5).
Statement 2: The points (0, 1) and (4/5, 3/5) lie on opposite sides of the line L and are at equal distance from it.
(a) Statement 1 is true, Statement 2 is false.
(b) Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation for Statement 1.
(c) Statement 1 is true, Statement 2 is true, Statement 2 is a correct explanation for Statement 1.
(d) Statement 1 is false, Statement 2 is true.

Question. If two vertical poles 20 m and 80 m high stand apart on a hori ontal plane, then the height (in m) of the point of intersection of the lines oining the top of each pole to the foot of other is
(a) 16
(b) 18
(c) 50
(d) 15

Question. Suppose that the points (h, k), (1, 2) and (– 3, 4) lie on the line L₁. If a line L₂ passing through the points (h, k) and (4, 3) is perpendicular on L₁, then equals :
(a) 1/3
(b) 0
(c) 3
(d) – 1/7

Question. If the line, 2x – y + 3 = 0 is at a distance 1/√5 and 2/√5 from the lines 4x – 2y + α = 0 and 6x – 3y + β = 0, respectively, then the sum of all possible value of α and β is ______.

Question. If the straight line, 2x – 3y + 17 = 0 is perpendicular to the line passing through the points (7, 17) and (15, β), then β equals :
(a) 35/3
(b) –5
(c) – 35/3
(d) 5

Question. The point of intersection of the lines (α³ + 3)x + αy + α – 3 = 0 and (α⁵ + 2)x + (α + 2)y + 2α + 3 = 0 (a real) lies on the y-axis for
(a) no value of α
(b) more than two values of α
(c) exactly one value of α
(d) exactly two values of α

Question. The perpendicular bisector of the line segment oining P (1, 4) and Q(k, 3) has y-intercept –4. Then a possible value of k is
(a) 1
(b) 2
(c) –2
(d) – 4

Question. A square of side a lies above the x-axis and has one vertex at the origin. The side passing through the origin makes an angle α(o < α < π/4) with the positive direction of x-axis. The equation of its diagonal not passing through the origin is
(a) y(cos α + sin α) + x(cos α – sin α) = α
(b) y(cos α – sin α) – x(sin α – cos α) = α
(c) y(cos α + sin α) + x(sin α – cos α) = α
(d) y(cos α + sin α) + x(sin α + cos α) = α

Question. The equation y = sin x sin (x + 2) – sin² (x + 1) represents a straight line lying in :
(a) second and third quadrants only
(b) first, second and fourth quadrant
(c) first, third and fourth quadrants
(d) third and fourth quadrants only

Question. If one of the lines of my² + (1– m²) xy – mx²= 0 is a bisector of the angle between the lines xy = 0, then m is
(a) 1
(b) 2
(c) –1/2
(d) –2

Question. If the sum of the slopes of the lines given by x² – 2cxy – 7y² = 0 is four times their product c has the value
(a) –2
(b) –1
(c) 2
(d) 1

Question. The lines p(p² +1)x – y + q = 0 and (p² + 1)²x + (p² + 1)y + 2q = 0 are perpendicular to a common line for :
(a) exactly one values of p
(b) exactly two values of p
(c) more than two values of p
(d) no value of p

Question. The shortest distance between the line y – x = 1 and the curve x = y² is :
(a) 2√3/8
(b) 3√2/5
(c) √3/4
(d) 3√2/8

Question. If the pair of straight lines x² – pxy – y² = 0 and x² – 2qxy – y² = 0 be such that each pair bisects the angle between the other pair, then
(a) pq = –1
(b) p = q
(c) p = –q
(d) pq = 1