Students should refer to Worksheets Class 11 Mathematics Straight Lines Chapter 10 provided below with important questions and answers. These important questions with solutions for Chapter 10 Straight Lines have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Straight Lines Worksheets Class 11 Mathematics
Question. The angle between the lines xy = 0 is equal to:
(a) 45°
(b) 60°
(c) 90°
(d) 180°
Answer
C
Question. If the line 2x + 3ay − 1 = 0 and 3x + 4y + 1 = 0 are mutually perpendicular, then the value of a will be:
(a) 1/2
(b) 2
(c) −1/2
(d) None of these
Answer
C
Question. If the line passing through (4, 3) and (2, k) is perpendicular to y = 2x + 3 , then k = ?
(a) –1
(b) 1
(c) – 4
(d) 4
Answer
D
Question. Let P(−1,0), Q(0,0) and R(3,3 3) be three points. Then the equation of the bisector of the angle PQR is:
(a) √3/2 x+y = 0
(b) x+√3y = 0
(c) √3x+y = 0
(d) x+√3/2 y = 0
Answer
C
Question. Equation of angle bisectors between x and y -axes are:
(a) y = ±x
(b) y = ±2x
(c) y = ± 1√2 x
(d) y = ±3x
Answer
A
Question. The bisector of the acute angle formed between the lines 4x − 3y + 7 = 0 and 3x − 4 y +14 = 0 has the equation:
(a) x + y + 3 = 0
(b) x − y − 3 = 0
(c) x − y + 3 = 0
(d) 3x + y − 7 = 0
Answer
C
Question. If the sum of the slopes of the lines given by x2 −2cxy−7y2 =0 is four times their product. Then c has the value:
(a) – 2
(b) – 1
(c) 2
(d) 1
Answer
C
Question. The straight lines 4ax + 3by + c = 0 where a + b + c = 0 , will be concurrent, if point is :
(a) (4, 3)
(b) (1/4, 1/3)
(c) (1/2, 1/3)
(d) None of these
Answer
B
Question. If the equation 12x2 −10xy + 2y2 +11x−5y+K=0 represent two straight lines, then the value of K is:
(a) 1
(b) 2
(c) 0
(d) 3
Answer
B
Question. The angle between the lines x2 − xy − 6y2 − 7x +31y −18 = 0 is:
(a) 45°
(b) 60°
(c) 90°
(d) 30°
Answer
B
Question. The new equation of curve 12x2 + 7xy −12y −17x − 31y −7 = 0 after removing the first degree terms:
(a) 12x2 − 7XY −12y2 = 0
(b) 12x2 + 7XY +12y2 = 0
(c) 12x2 + 7XY −12y2 = 0
(d) None of these
Answer
C
Question. Distance between the pair of lines represented by the equation 2x2 − 6xy + 9y2 + 3x − 9y − 4 = 0 ?V
(a) 15/√10
(b) 1/2
(c)√(5/2)
(d) 1/√10
Answer
C
Question. The angle between the pair of straight lines represented by 2x2 − 7xy + 3y2 = 0 is:
(a) 60º
(b) 45º
(c) tan–1 (7/6)
(d) 30º
Answer
B
Question. The equation of the bisectors of the angles between the lines represented by x2 + 2xy cotθ + y2 = 0 is:
(a) x2 − y2 = 0
(b) x2 − y2 = xy
(c) (x2 − y2 )cotθ = 2xy
(d) None of these
Answer
A
Question. The point of intersection of the lines represented by the equation 2x2 + 3y2 + 7xy + 8x +14y + 8 = 0 is:
(a) (0,2)
(b) (1,2)
(c) (–2, 0)
(d) (–2,1)
Answer
C
Question. A triangle with vertices (4, 0); (–1, –1); (3, 5) is:
(a) Isosceles and right angled
(b) Isosceles but not right angled
(c) Right angled but not isosceles
(d) Neither right angled nor isosceles
Answer
A
Question. The co-ordinate of the point dividing internally the line joining the points (4,–2) and (8,6) in the ratio 7: 5 will be:
(a) (16, 18)
(b) (18, 16)
(c) (19/3 , 8/3)
(d) (8/3 , 19/3)
Answer
C
Question. If the pair of straight lines xy − x − y +1 = 0 and line ax + 2 y − 3 = 0 are concurrent, then a =?
(a) – 1
(b) 0
(c) 3
(d) 1
Answer
D
Question. The lines joining the origin to the point of intersection of the circle x2 + y2 = 3 and the line x + y = 2 are:
(a) y − (3 + 2√2)x = 0
(b) x − (3 + 2√2) y = 0
(c) x − (3 − 2√2) y = 0
(d) y − (3 − 2√2)x = 0
Answer
ALL
Question. The pair of straight lines joining the origin to the points of intersection of the line y = 2√2x + c and the circle x2 + y2 = 2 are at right angles, if:
(a) 2 c − 4 = 0
(b) 2 c − 8 = 0
(c) 2 c − 9 = 0
(d) 2 c −10 = 0
Answer
C
Question. The coordinates of the foot of perpendicular drawn from (2, 4) to the line x + y =1 is:
(a) (1/3 , 3/2)
(b) (−1/2 , 3/2)
(c) (4/3 , 1/2)
(d) (3/4 , −1/2)
Answer
B
Question. The area enclosed within the curve | x | + | y |=1 is:
(a) 2
(b) 1
(c) 3
(d) 2
Answer
D
Question. The area of the triangle formed by the lines 4x2 −9xy−9y2 = 0 and x = 2 is:
(a) 2
(b) 3
(c) 10/3
(d) 20/3
Answer
C
Question. The gradient of the line joining the points on the curve y2 = x + 2x , whose abscissae are 1 and 3, is:
(a) 6
(b) 5
(c) 4
(d) 3
Answer
A
Question. Equation to the straight line cutting off an intercept 2 from the negative direction of the axis of y and inclined at 30° to the positive direction of x, is:
(a) y + x − 3 = 0
(b) y − x + 2 = 0
(c) y − √3x − 2 = 0
(d) √3y − x + 2√3 = 0
Answer
D
Question. The point on the x-axis whose perpendicular distance from the line x/a + y/b = 1 is a, is:
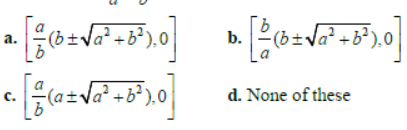
Answer
A
Question. The vertex of an equilateral triangle is (2, –1) and the equation of its base is x + 2y =1.The length of its sides is:
(a) 4/√15
(b) 2/√15
(c) 4/3√3
(d) None of these
Answer
B
Question. The reflection of the point (4,–13) in the line 5x+y+6=0 is:
(a) (–1, –14)
(b) (3, 4)
(c) (1, 2)
(d) (–4, 13)
Answer
A
Question. If the lines 4x+3y =1, y = x+5 and 5y + bx = 3 are concurrent, then b equals:
(a) 1
(b) 3
(c) 6
(d) 0
Answer
C
Question. If the lines ax+by+c=0, bx+cy+a=0 and cx + ay + b = 0 be concurrent, then:
(a) a3 + b3 + c3 + 3abc = 0
(b) a3 + b3 + c3 – abc = 0
(c) a3 + b3 + c3 – 3abc = 0
(d) None of these
Answer
C
QuestionLet L1 be a straight line passing through the origin and L2 be the straight line x + y = 1. If the intercepts made by the circlex2 + y2 – x + 3y = 0 on L1 and L2 are equal, then
which of the following equation can represent L1?
(a) x + y = 0
(b) x –y = 0
(c) x +7y = 0
(d) x –7y = 0
Answer
A,C
Question. Two roads are represented by the equations y − x = 6 and x + y = 8.An inspection bunglow has to be so constructed that it is at a distance of 100 from each of the roads.
Possible location of the bunglow is given by:
(a) (100√3 +1,7)
(b) (1−100√2,7)
(c) (1,7 +100√2)
(d) (1,7 −100√2)
Answer
ALL
Question. The point (3, 2) is reflected in the y-axis and then moved a distance 5 units towards the negative side of y-axis. The co-ordinate of the point thus obtained are:
(a) (3, –3)
(b) (–3, 3)
(c) (3, 3)
(d) (–3, –3)
Answer
D
Question. Let A (2,–3) and B(–2,1) be vertices of triangle AB(c) If the centroid of this triangle moves on the line 2x + 3y = 1 , then the locus of the vertex C is the line:
(a) 3x − 2y = 3
(b) 2x − 3y = 7
(c) 3x + 2y = 5
(d) 2x + 3y = 9
Answer
D
Question. The equation of the bisector of the angles between the two intersecting lines
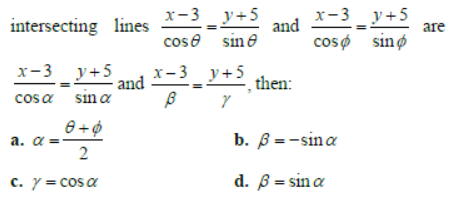
Answer
A,B,C
Question. A line which makes an acute angle θ with the positive direction of x-axis is drawn through the point P(3,4) to meet the line x = 6 at R and y = 8 at S, then:
(a) PR = 3 sec θ
(b) PS = 4 cosec θ
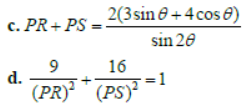
Answer
ALL
Question. The centroid of a triangle is (2,7)and two of its vertices are (4, 8) and (–2, 6) the third vertex is:
(a) (0, 0)
(b) (4, 7)
(c) (7, 4)
(d) (7, 7)
Answer
B
Question. If the vertices of a triangle be (2, 1); (5, 2) and (3,4) then its circumcentre is:
(a) (13/2 , 9/2)
(b) (13/4 , 9/4)
(c) (9/4 , 13/4)
(d) None of these
Answer
B
Question. Equation of the straight line, inclined at 30° to the axis of x such that the length of its (each of their) line segment between the coordinate axes is 10 units, is: (are)
(a) x − √3y − 5√3 = 0
(b) x − y/√3 − 5√3 = 0
(c) x − √3y + 5√3 = 0
(d) x − y/√3 + 5√3 = 0
Answer
A,C
Question. Let L be the line 2x + y = 2. If the axes are rotated by 45°, then the intercept made by the line L on the length of new axes are respectively:
(a) √2 and 1
(b) 1 and √2
(c) 2√2 and 2√2/3
(d) 2√2/3 and 2√2
Answer
C,D
Question. The reflection of the point (4,–13) in the line 5x+y+6=0 is:
(a) (–1, –14)
(b) (3, 4)
(c) (1, 2)
(d) (–4, 13)
Answer
A
Question. The image of a point A(3,8) in the line x + 3y − 7 = 0 , is:
(a) (–1, –4)
(b) (–3, –8)
(c) (1, –4)
(d) (3, 8)
Answer
A
Assertion and Reason
Note: Read the Assertion (A) and Reason (R) carefully to mark the correct option out of the options given below:
(a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
(c) If assertion is true but reason is false.
(d) If the assertion and reason both are false.
e. If assertion is false but reason is true.
Question. Consider the lines L1:p2x + py –1=0; L2: q2x +qy +6=0;L1 passes through the point (3, 2) and L2 passes through the point (2, 7):
Assertion: If the product of the slopes of L1 and L2 is 2 then they intersect at the point (–4, –5)
Reason: L1and L2 are neither parallel nor perpendicular
Answer
C
Question. Assertion: 4x2 + 12xy + 9y2 = 0 represents a pair of perpendicular lines through the origin.
Reason: ax2 + 2hxy + by2 = 0 represents a pair of coincident lines if h2 = a(b)
Answer
D
Question. Assertion: x2y2 – x2 – y2 + 1 = 0 represents the sides of a square of area 4 square units.
Reason: 3x2 + λxy – 3y2 = 0 represents a pair of perpendicular lines for all values of λ.
Answer
B
Question. Assertion: Consider the point A(0,1) and B(2,0) and P be point on the line 4x+ 3y + 9= 0, then the coordinates of P such that |PA –PB| is maximum is (–24/5 , 17/5)
Reason: If A and B are tow fixed point and P is any point in a plane, then |PA –PB| ≤ A(b)
Answer
A
Question. Assertion: If the circumcentre of a triangle lies at the origin and centroid is the mid point of the line joining the points (2,3) and (4,7), then its orthocenter line 5x – 3y = 0.
Reason: Circumcentre, centroid and orthocenter of a triangle lie on the same line.
Answer
A
Question. Let A(2,–3) and B(–2,1) be the vertices of a triangle ABC:
Assertion: If the centroid of the triangle moves on the line x + y =5, the vertex moves on the line x + y = 17.
Reason: If the centroid of the triangle moves the line x – y + 1 = 0 (x ≠ 0), the triangle is either isosceles or equilateral.
Answer
B
Question. Assertion: x2 y − 3xy − 2×2 + 6x − 4y + 8 = 0 represents three straight lines two of which are parallel and the third is perpendicular to the other two
Reason: xy − 2x + y − 2 = 0 represents a pair of straight lines one of which is common to the pair of straight lines xy + 2x – y = 0
Answer
C
Question. Assertion: If the perpendicular bisector of the line segment joining P(1,4) and Q(k,3) has y-intercept equal to –4, then k2 – 16 = 0
Reason: Centroid of an isosceles triangle ABC lies on the perpendicular bisector of the base BC where B = (c)
Answer
B
Question. Assertion
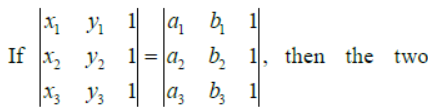
triangle with vertices (x1, y1), (x2, y2), (x3, y3) and (a1, b1), (a2, b2), (a3, b3) must be congruent
Reason: Two congruent triangles have the same are(a)
Answer
D
Question. Assertion: If x +ky = 1and x = a are the equations of the hypotenuse and a side of a right angled isosceles triangle then k = ± (a)
Reason: Each side of a right angled isosceles triangle makes an angle π/4 with the hypotenuse.
Answer
D
Comprehension Based
Paragraph –I
Let a,r,s,t be non-zero real numbers. Let P(at2, 2at), Q,R(ar2, 2ar), and S(as2,2as) be distinct point on the parabola y2 = 4 ax.
Suppose that PQ is the focal chord and line QR and PK are parallel, where K is the point (2a, 0).
Question. The value of r is:
(a) −1/t
(b) t2 +1/t
(c) 1/t
(d) t2 −1/t
Answer
D
Question. If st = 1, then the tangent at P and the normal at S to the parabola meet at a point whose ordinate is:
(a) (t2 +1/t)2t3
(b) a(t2 +1)2t3
(c) a(t2 +1)2/t3
(d) a(t2 +2)2/t3
Answer
B
Paragraph –II
Let P(x, y) be the Cartesian coordinates with respect to axes OX and OY, then (r,θ) be its polar coordinates with respect to pole O and initial line OX i.e., OP = r (radius vector) and
∠XOP = θ (vectorial angle). Now let p be the length of perpendicular form O upon straight line (through A, B) ie., OM = p and ∠XOM = α We, have OM = OP cos (θ – α) or p = r cos
(θ – α) which is the required equation to the given line.
Question. Cartesian form of the curve √r = √asin (θ / 2), ∀ a > 0 is:
(a) 4(x2 – y2)(x2 + y2 + ax) = a2y2
(b) 4(x2 – y2)(x2 + y2 – ax) = a2y2
(c) 4(x2 + y2)(x2 + y2 + ax) = a2y2
(d) 4(x2 + y2)(x2 + y2 – ax) = a2y2
Answer
C
Question. Polar form of the curve x3 + 3x2 y – 3xy2 – y3 = 5kxy is:
(a) 2r (cos 3θ + sin 3θ) = 5k sin θ cos θ
(b) r (cos 3θ + sin 3θ) = 5k sin θ cos θ
(c) 2r (cos 3θ – sin 3θ) = 5k sin θ cos θ
(d) r (cos 3θ – sin 3θ) = 5k sin θ cos θ
Answer
B
Question. Locus of the point P(r,θ ), if 2/r = −1/2 + 4cosθ is an:
(a) circle
(b) parabola
(c) ellipse
(d) hyperbola
Answer
D
Question. If 1/r = f(θ) where f (θ ) = acos(θ +α)+bcos(θ +β ), represents a straight line and that any line perpendicular to it is:
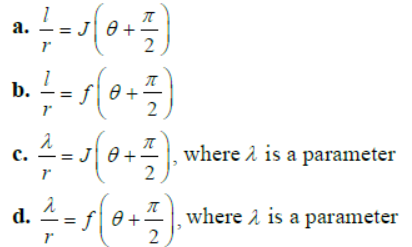
Answer
C
Question. If (1, π/6), (2, π/3) and (3, π/2) be the angular points of a triangle. Then the area of the triangle is:

Answer
D
Match the Column
Question. Match the statement of Column with those in Column II:

(a) A→3,5, B→1,2 C→2,4
(b) A→3,5, B→1,4, C→2
(c) A→1,4 B→3,2 C→2,4
(d) A→1,4, B→2,3, C→3
Answer
B
Question. Consider the lines given by L1: x + 3y – 5 = 0; L2: 3x – ky – 1 = 0; L3: 5x + 2y – 12 = 0

(a) A→4, B→1,2 C→3, D→1,2,4
(b) A→1,2, B→4, C→3, D→1,4
(c) A→1,3, B→2, C→4, D→1,3,4
(d) A→4, B→2,3, C→4, D→2
Answer
A