Please refer to Class 12 Mathematics Sample Paper Set O with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
1.
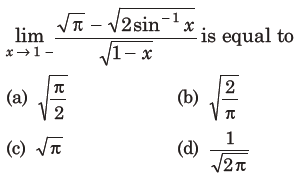
Answer
B
2. Let S be the set of all real values of λ such that a plane passing through the points (- λ2,1,1), (1-λ2.1) and (1,1-λ2) also passes through the point (- 1,-1, 1). Then, S is equal to
(a) { √3, – √3}
(b) {√3, – √3}
(c) {1, – 1}
(d) { √3}
Answer
A
3. If a circle of radius R passes through the originO and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is
(a) (x2+ y2 )2 =4R2x2y2
(b) (x2+y2)3=4R2x2y2
(c) (x2+y2)(x+y)=R2xy
(d) (x2+y2)2=4Rx2y2
Answer
B
4. If an angle between the line,x +1/2=y-2/1= z-3/-2 and the plane,x – 2y – kz = 3 is cos-1(2√2/3), then a value of k is
(a)√5/3
(b)√3/5
(c) – 3/5
(d) – 5/3
Answer
A
5. The expression ~ (~ p→ q) is logically equivalent to
(a) p ∧ ~ q
(b) p ∧ q
(c) ~ p ∧ q
(d) ~ p ∧~ q
Answer
D
6. The set of all values of l for which the system of linear equations x – 2y – 2z = λx, x + 2y + z = λy and – x – y = λz has a non-trivial solution
(a) contains exactly two elements.
(b) contains more than two elements.
(c) is a singleton.
(d) is an empty set.
Answer
C
7. Let Z be the set of integers. If

number of subsets of the set A x B, is
(a) 212
(b) 218
(c) 215
(d) 210
Answer
C
8. In a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then the probability that the student selected has opted neither for NCC nor for NSS is
(a)1/6
(b)1/3
(c)2/3
(d)5/6
Answer
A
9. If a curve passes through the point (1,- 2) and has slope of the tangent at any point (x, y) on it as x2-2y/x, then the curve also passes through the point
(a) ( √3, 0)
(b) (- 1, 2)
(c) (- √2, 1)
(d) (3, 0)
Answer
A
10.

is equal to
(a) tan- 1 (3 )
(b) tan- 1 (2)
(c) π / 4
(d) π /2
Answer
B
11. In a game, a man wins `R.s.100 if he gets 5 or 6 on a throw of a fair die and loses `50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is
(a)400/3 loss
(b)400/9 loss
(c) 0
(d)400/3 gain
Answer
C
12. If sin4 α + 4cos4 β + 2 = 4 √2sin α cos β;α β ∈[0, π], then cos(α + β) – cos(α – β) is equal to
(a) – 1
(b) 2
(c) – 2
(d) 0
Answer
C
13. If the function f given by f (x) = x3 -3 (a -2 ) x2 + 3ax +7,for some a ∈R is increasing in (0, 1] and decreasing in [1, 5), then a root of the equation,f (x)-14/(x-1)2=0(x≠1) is
(a) – 7
(b) 6
(c) 7
(d) 5
Answer
C
14. If nC4, nC5 and nC6 are in AP, then n can be
(a) 9
(b) 11
(c) 14
(d) 12
Answer
C
15. Let f be a differentiable function such that f (1) = 2 and f’ (x)(x) = f (x) for all x∈R. If h(x) = f (f (x)), then h'(1) is equal to
(a) 4 e2
(b) 4e
(c) 2e
(d) 2 e2
Answer
B
16. The mean and the variance of five observations are 4 and 5.20,respectively. If three of the observations are 3, 4 and 4, then the absolute value of the difference of the other two observations, is
(a) 1
(b) 7
(c) 5
(d) 3
Answer
B
17. The number of integral values of m for which the quadratic expression, (1+ 2m ) x2-2(1+ 3m ) x+4(1+m),x ∈ R, is always positive, is
(a) 6
(b) 8
(c) 7
(d) 3
Answer
C
18. The total number of irrational terms in the binomial expansion of (71/5-31/10)60 is
(a) 49
(b) 48
(c) 54
(d) 55
Answer
C
19.
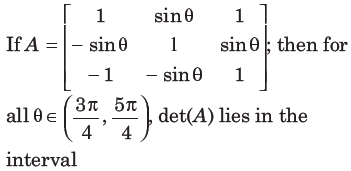

Answer
A
20. Let a, band c be three unit vectors, out of which vectors band c are non-parallel. If α and β are the angles which vector a makes with vectors b and crespectively and a x (b x c) = 1/2 b,, then|α – β|is equal to
(a) 30º
(b) 45º
(c) 90º
(d) 60º
Answer
A
21. If the sum of the first 15 terms of the series

is equal to 225 k, then k is equal to
(a) 108
(b) 27
(c) 54
(d) 9
Answer
B
22.
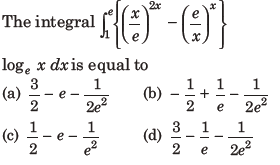
Answer
A
23. The integral

Answer
B
24. The tangent to the curve y = x2 – 5x + 5, parallel to the line 2y = 4x + 1, also passes through the point
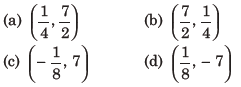
Answer
D
25. Let z1 and z2 be two complex numbers satisfying|z1| 1 = 9 and |z2-3-4i|=4. Then, the minimum value of|z1-z2| is
(a) 1
(b) 2
(c) √2
(d) 0
Answer
D
26. The equation of a tangent to the parabola, x2 = 8y, which makes an angle q with the positive direction of X-axis, is
(a) y = x tanθ – 2 cot θ
(b) x = y cotθ + 2 tan θ
(c) y = x tanθ + 2 cot θ
(d) x = y cotθ – 2 tan θ
Answer
B
27. If the angle of elevation of a cloud from a point P which is 25 m above a lake be 30º and the angle of depression of reflection of the cloud in the lake from P be 60º, then the height of the cloud (in meters) from the surface of the lake is
(a) 50
(b) 60
(c) 45
(d) 42
Answer
A
28. Let S and S’ be the foci of an ellipse and B be any one of the extremities of its minor axis. If ΔS’BS is a right angled triangle with right angle at B and area (ΔS’BS) = 8 sq units, then the length of a latus rectum of the ellipse is
(a) 2√2
(b) 4√2
(c) 2
(d) 4
Answer
D
29. There are m men and two women participating in a chess tournament.
Each participant plays two games with every other participant. If the number of games played by the men between themselves exceeds the number of games played between the men and the women by 84, then the value of m is
(a) 12
(b) 11
(c) 9
(d) 7 A
30. If a straight line passing through the point P(- 3, 4) is such that its intercepted portion between the coordinate axes is bisected at P, then its equation is
(a) x – y + 7 = 0
(b) 4x – 3y + 24= 0
(c) 3x – 4y + 25 = 0
(d) 4x + 3y = 0 B