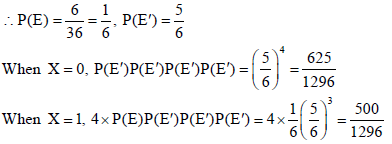Please refer to Class 12 Mathematics Sample Paper Set F with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
SECTION A
Question numbers 01 to 20 carry 1 mark each.
1. The relation R in the set {1, 2, 3} given by R = {(1,2),(2,1), (1,1)} is
(a) symmetric and transitive, but not reflexive
(b) reflexive and symmetric, but not transitive
(c) symmetric, but neither reflexive nor transitive
(d) an equivalence relation
Answer
C
2. tan −1 3 + tan−1 λ = tan−1 (3 + λ/1 − 3λ) is valid for what values of λ ?
(a) λ ∈ (−1/3)
(b) λ > 1/3
(c) λ < 1/3
(d) All real values of λ
Answer
C
3. If A is a non-singular square matrix of order 3 such that A2 = 3A, then value of |A|is
(a) –3
(b) 3
(c) 9
(d) 27
Answer
D
4. The function f : R → R given by f (x) = – |x –1| is
(a) continuous as well as differentiable at x =1
(b) not continuous but differentiable at x =1
(c) continuous but not differentiable at x =1
(d) neither continuous nor differentiable at x =1
Answer
C
5. Let A ={1, 3, 5}. Then the number of equivalence relations in A containing (1, 3) is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
6. The interval in which the function f given by f (x) = x2e–x is strictly increasing, is
(a) (–∞, ∞)
(b) (–∞, 0)
(c) (2, ∞)
(d) (0, 2)
Answer
D
7. If |a̅| = 4 and –3 ≤ λ ≤ 2 then |λa̅| lies in
(a) [0,12]
(b) [2,3]
(c) [8,12]
(d) [–12,8]
Answer
A
8. The vectors 3î – ĵ+ 2k̂, 2î + ĵ+ 3k̂ and î + λĵ– k̂ are coplanar if value of λ is
(a) –2
(b) 0
(c) 2
(d) Any real number
Answer
A
9. The area of a triangle formed by vertices O, A and B, where O̅A̅ = î + 2ĵ+ 3k̂ and O̅B̅ = –3î – 2ĵ+ k̂ is
(a) 3√5 sq. units
(b) 5√5 sq. units
(c) 6√5 sq. units
(d) 4 sq. units
Answer
A
10. The coordinates of the foot of the perpendicular drawn from the point (2, –3, 4) on the y-axis is
(a) (2, 3, 4)
(b) (–2, –3, –4)
(c) (0, –3, 0)
(d) (2, 0, 4)
Answer
C
Fill in the blanks
11. The range of the principal value branch of the function y = sec–1 x is __________.
Sol. [0,π] – {π/2}
OR
The principal value of cos–1 (–1/2) is ________.
Sol. cos–1 (–1/2) = π – cos–1 (1/2) = π – π/3 = 2π/3.
12. Given a skew-symmetric matrix
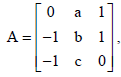
the value of (a + b + c)2 is _______.
Sol. As A is skew-symmetric matrix so, aij = –aji .
Now a12 = –a21 ⇒ a = –(–1) =1, a32 = –a23 ⇒ c = –1.
Also all the diagonal elements in A must be 0 so, b = 0 .
Now (a + b + c)2 = (1+ 0 –1)2 = 0.
13. The distance between parallel planes 2x + y – 2z – 6 = 0 and 4x + 2y – 4z = 0 is _______ units.
Sol. Rewriting second plane to get 2x + y – 2z = 0
Distance between 2x + y – 2z – 6 = 0 and 2x + y – 2z = 0 is
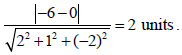
OR
If P(1, 0, –3) is the foot of the perpendicular from the origin to the plane, then the Cartesian
equation of the plane is ____________.
Sol. Note that OP will act as the normal to the plane.
The d.r.’s of normal to the plane are 1, 0, –3.
Required equation : 1(x –1) + 0(y – 0) + (–3)(z + 3) = 0 i.e., x – 3z =10 .
14. If the radius of the circle is increasing at the rate of 0.5 cm/s, then the rate of increase of its circumference is _______.
Sol. Circumference of circle, C = 2πr
⇒ dC/dt = 2π dr/dt
⇒ dC/dt = 2π × 0.5 = π cm s–1 [∴ dr/dt = 0.5 cm s–1
15. The corner points of the feasible region of an LPP are (0, 0), (0, 8), (2, 7), (5, 4) and (6, 0). The maximum profit P = 3x + 2y occurs at the point ____________.
Sol. Note that P(0,0) = 0, P (0,8) = 16,P (2,7) = 20, P (5,4) = 23, P(6,0) =18 .
Clearly the maximum profit occurs at (5, 4).
Question numbers 16 to 20 are of very short answer type questions.
16. Differentiate sec2 (x2 ) with respect to x2 .
Sol.
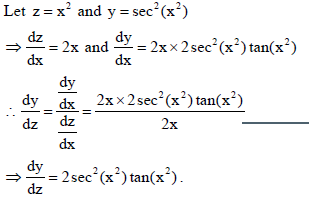
OR
If y = f (x2 ) and f'(x) = e√x , then find dy/dx.
Sol. y = f (x2 )
⇒ dy/dx = f'(x2) × 2x
⇒ dy/dx = e√x² × 2x = 2xex
17. Find the value of k, so that the function
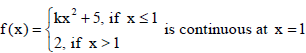
Sol. As f (x) is continuous at x =1 so, limx→1¯ f(x) = limx→1+f(x) = f(1)
⇒ limx→1+ (2) = k(1)2 + 5
⇒ 2 = k + 5
∴ k = –3.
18. Evaluate :
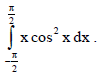
Sol. Let f (x) = x cos2 x
⇒ f (–x) = –x cos2 (–x) = –x cos2 x = –f (x) .
Note that x cos2 x is odd function.
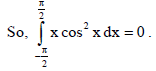
19. Find the general solution of the differential equation ey–x dy/dx = 1.
Sol. ey–x dy/dx = 1
⇒ ∫ey dy = ∫ex dx
⇒ ey = ex + C .
20. Find the coordinates of the point where the line
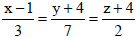
cuts the xy-plane.
Sol.
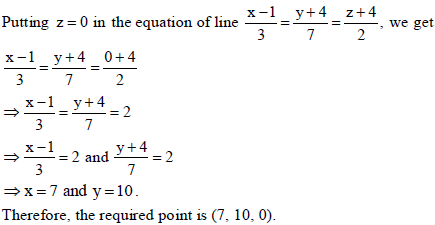
SECTION B
Question numbers 21 to 26 carry 2 marks each.
21.
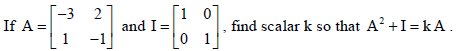
Sol.
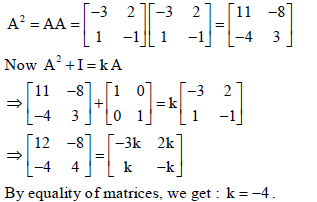
22.
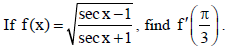
Sol.
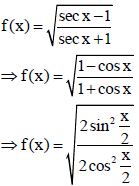
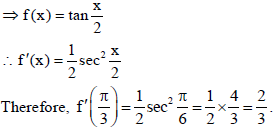
OR
Find f ‘(x) , if f (x) = (tan x)tan x .
Sol.f (x) = (tan x)tan x
⇒ log f (x) = log(tan x)tan x
⇒ log f (x) = tan x log(tan x)
⇒ 1/f(x) × f'(x) = tanx × 1/tanx × sec2x + log(tan x) × sec2x
⇒ f ‘(x) = (tan x)tan x (1+ log tan x) × sec2x
23. Find :
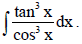
Sol.
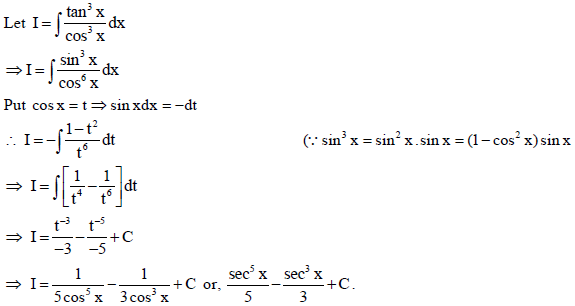
24. Find a vector r̅ equally inclined to the three axes and whose magnitude is 3√3 units.
Sol.
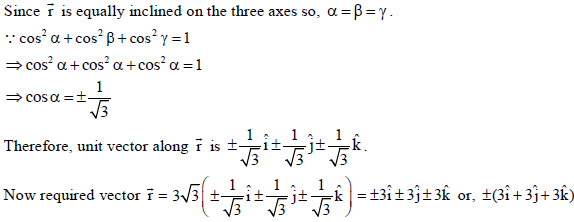
OR
Find the angle between unit vectors a̅ and b̅ so that √3 a̅ – b̅ is also a unit vector.
Sol. As |√3 a̅ – b̅| =1
⇒ |√3 a̅ – b̅|2 =12
⇒(√3 a̅ – b̅).(√3 a̅ – b̅) = 1
⇒ 3|a̅|2 – 2√3 a̅.b̅ + |b̅|2 =1
⇒ 3×12 – 2√3| a̅||b̅|cosθ +12 =1, where θ is the required angle
⇒–2√3×1×1×cosθ = –3
⇒ cosθ = √3/2
∴ θ = π/6.
25. Find the points of intersection of the line r̅ = 2î – ĵ+ 2k̂ + λ(3î + 4ĵ+ 2k̂) and the plane
r̅ .(î – ĵ+ k̂ ) = 5.
Sol. Any point on the given line is r̅ = (2 + 3λ)î + (–1+ 4λ)ĵ+ (2 + 2λ)k̂ …(i)
When the line intersects plane r̅ .(î – ĵ + k̂ ) = 5 then,
[(2 + 3λ)î + (–1+ 4λ)ĵ+ (2 + 2λ)k̂ ].(î – ĵ+ k̂ ) = 5
⇒ (2 + 3λ) – (–1+ 4λ) + (2 + 2λ) = 5
⇒ λ = 0
On putting value of λ in (i), we get r̅ = 2î – ĵ+ 2k̂ .
Therefore the required point is (2, –1, 2).
26. A purse contains 3 silver and 6 copper coins and a second purse contains 4 silver and 3 copper coins. If a coin is drawn at random from one of the two purses, find the probability that it is a silver coin.
Sol. Let E1 : coin is drawn from first purse and E2 : coin is drawn from second purse.
Also let A : silver coin is drawn.
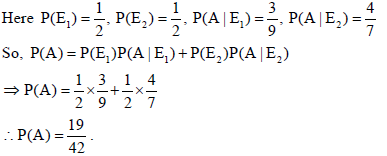
SECTION C
Question numbers 27 to 32 carry 4 marks each.
27. Check whether the relation R in the set N of natural numbers given by
R = {(a, b) : a is divisor of b}
is reflexive, symmetric or transitive. Also determine whether R is an equivalence relation.
Sol. Reflexive: For any a ∈ N, we always have (a,a)∈ R Since a always divides a. Thus, R is reflexive.
Symmetric: For (1, 2)∈ R , we mean 1 divides 2, which is true.
But (2,1)∉ R as 2 doesn’t divide 1.
So, (a, b)∈ R does not imply (b,a) ∈ R .
∴ R is not symmetric .
Transitive: For any a, b,c ∈ N, let (a, b)∈ R and (b,c) ∈ R .
That is, a divides b; b divides c.
It means, a also divides c.
That is, (a, c)∈R .
∴ R is transitive
Therefore, R is not an equivalence relation as, it is not symmetric.
OR
Prove that tan–11/4 + tan–12/9 = 1/2 sin–14/5
Sol.
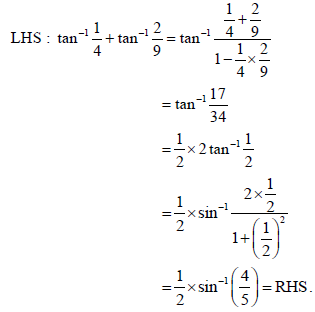
28.
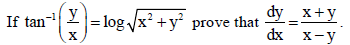
Sol.
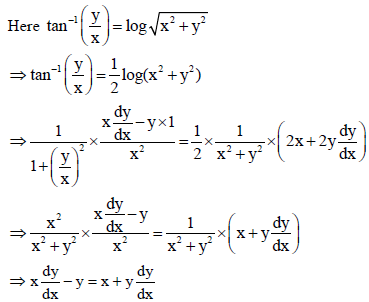
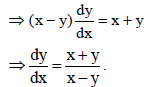
OR
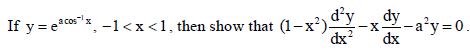
Sol.
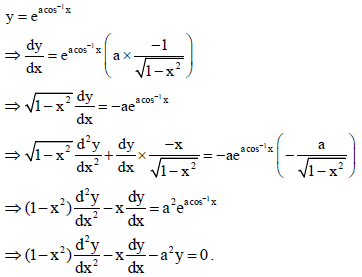
29. Find :
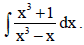
Sol.

30. Solve the differential equation :
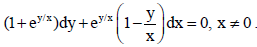
Sol.

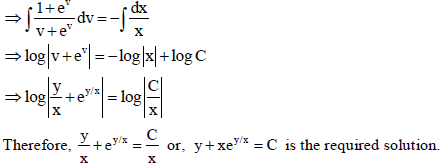
31. Find the shortest distance between the lines
r̅ = 2î – ĵ+ k̂ + λ(3î – 2ĵ+ 5k̂) ,
r̅ = 3î + 2ĵ– 4k̂ + μ(4î – ĵ+ 3k̂) .
Sol. Given line are
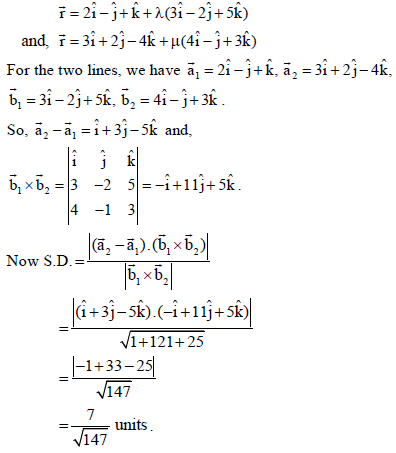
32. A cottage industry manufactures pedestal lamps and wooden shades. Both the products require machine time as well as craftsman time in the making. The number of hour (s) required for producing 1 unit of each and the corresponding profit is given in the following table :

In a day, the factory has availability of not more than 42 hours of machine time and 24 hours of
craftsman time.
Assuming that all items manufactured are sold, how should the manufacturer schedule his daily
production in order to maximize the profit?
Formulate it as an LPP and solve it graphically.
Sol. Let number of pedestal lamps be x and that of wooden shades be y.
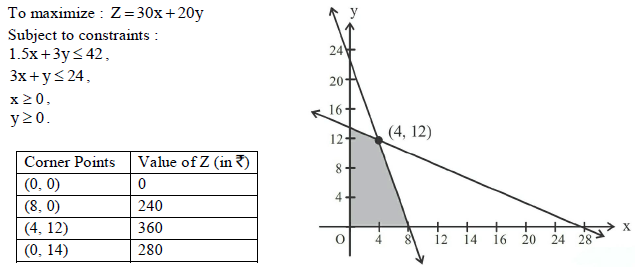
Maximum profit is Rs 360.
Number of pedestal lamps = 4 , and number of wooden shades =12 .
SECTION D
Question numbers 33 to 36 carry 6 marks each.
33.
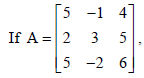
then find A–1 and use it to solve the following system of the equations:
5x – y + 4z = 5,
2x + 3y + 5z = 2,
5x – 2y + 6z = –1.
Sol.
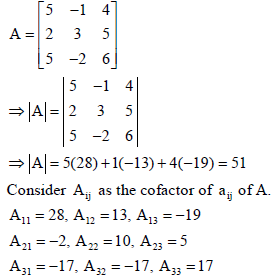

OR
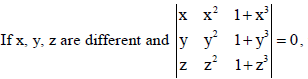
then using properties of determinants show that 1+ xyz = 0.
Sol.
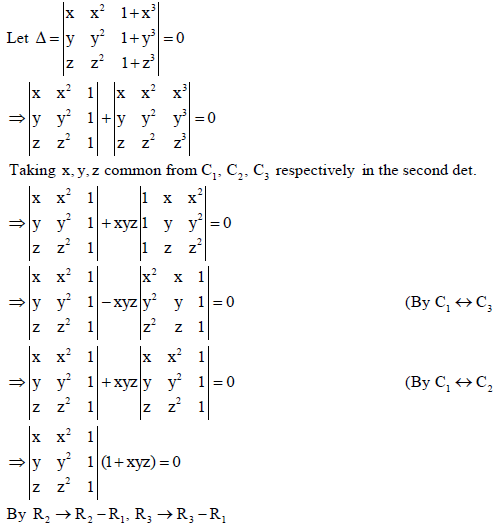
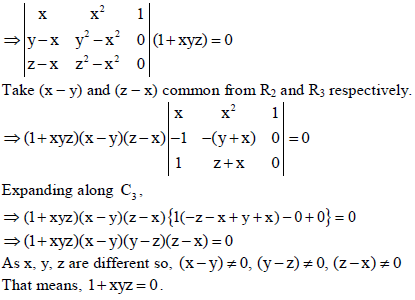
34. Amongst all open (from the top) right circular cylindrical boxes of volume 125 π cm3 , find the dimensions of the box which has the least surface area.
Sol. Let radius be r and height be h.
Given that volume is, 125π = πr2h
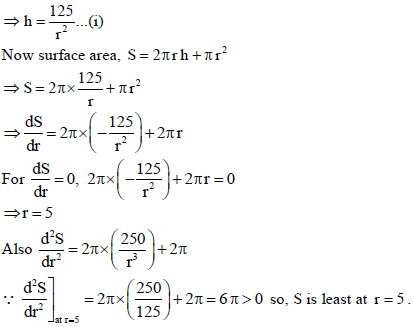
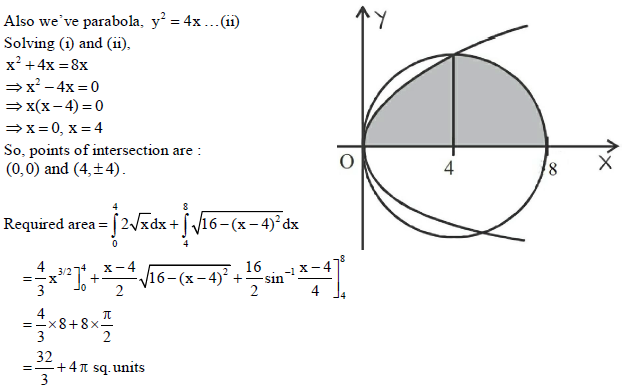
35. Using integration, find the area lying above x-axis and included between the circle x2 + y2 = 8x and inside the parabola y2 = 4x .
Sol. We havex2 + y2 = 8x…(i)
⇒ x2 –8x +16 + y2 =16
⇒ (x – 4)2 + (y – 0)2 = 42
∴ Centre is at (4, 0) and r = 4
OR
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B(4, 5) and C(6, 3).
Sol.

36. Find the probability distribution of the random variable X, which denotes the number of doublets in four throws of a pair of dice. Hence, find the mean of the number of doublets (X).
Sol. As X denotes the number of doublets in four throws of a pair of dice so, X = 0, 1, 2, 3, 4 .
Let E : doublet appears on the die