VBQs Conic Sections Class 11 Mathematics

VBQs Conic Sections Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Conic Sections Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.

Conic Sections VBQs Class 11 Mathematics

Question: The focus of the parabola y²=4y-4x is
(a) (0, 2)
(b) (1, 2)
(c) (2, 0)
(d) (2, 1) 

Question: The equation represents λX²+4XY+Y²+λx+3Y+2=0 represents a parabola, if λis
(a) -4
(b) 4
(c) 0
(d) None of these 

Question: The focus of the parabola y²=4y-4x  is
(a) (0, 2)
(b) (1, 2)
(c) (2, 0)
(d) (2, 1) 

Question: The equation represents λX²+4XY+Y²+λx+3Y+2=0 represents a parabola, if λis
(a) -4
(b) 4
(c) 0
(d) None of these 

Question: The length of latusrectum of the parabola 169 {(x-1)² +(y-3)²}= (5x-12y+17)² is
(a) 14/13
(b) 28/13
(c) 12/13
(d) None of these 

Question: If the point P( 4,2 ) is one end of the focal chord PQ of the parabola y2=x, then the slope of the tangent at Q is
(a) -1/4
(b) 1/4
(c) 4
(d) -4  

Question: x-2=t²,y=2t are the parametric equations of the parabola
(a) y²=4x
(b) y²=-4x 
(c) x²=-4y 
 (d) y²=4(x-2) 

Question: The equation of the parabola having vertex at the origin axis on the y-axis and passing through the point( , ) 6 3 – is
(a) y²=12x +6 
(b) x²= 12y
(c) x² = 12y 
(d) y² = 12x+6 

Question: If the vertex of a parabola is the point( -3,0 )  and the directrix is the line x +5 =0, then equation of parabola is
(a) y² = 8(x+3)
(b) x2 = 8(y+3)
(c) y2 = -8(8+3)
(d) y2 = 8(x+5)   

Question: The equation of parabola having vertex (0,0), passing through (5, 2) and symmetric with respect to y-axis is
(a) 3x² =25y 
(b) 2x² = 25y 
(c) 2y² = 25y 
(d) None of these 

Question: The latusrectum of the parabola y²=5x+4y+1 is 
(a) 5/4
(b) 10
(c) 5
(d) 5/2 

Question: A tangent to a parabola y² = 4ax is inclined at π/3 with the axis of the parabola. The point of contact is
(a) (a/3,- 2a/√3)
 (b) (3a,-2√3a)
(c) (3a,2√3a)
(d) None of these 

Question: If the normal to the parabola y² = 4ax at the point P (at²,2at)  cuts the parabola again at Q(aT², 2aT), then
(a) -2≤ t ≤ 2
(b) t ∈(-∞,-8) ∪ (8,∞)
(c) T2 <8
(d) T2 ≥8 

Question: The tangents and normal at the ends of the latusrectum of a parabola form a
(a) cyclic quadrilateral
(b) rectangle
(c) square
(d) None of these 

Question: The locus of the middle points of the focal chords of parabola y²= 4ax is
(a) y² = a(x-a)
(b) y² = 2a(x-a)
(c) y² = 4a(x-a) 
 (d) None of these 

Question: If tangents at A and B on the parabola y² = 4ax   intersect at point C, then ordinates of A C, and B are
(a) always in AP
(b) always in GP
(c) always in HP
(d) None of these 

Question: The equation of tangent to the parabola y²=9x which goes through the point (4, 10) is
(a) x+ 4y +1=0
(b) 9x + 4y + 4=0 
(c) x- 4y+ 36 = 0
(d) 9x + 4y+9=0 

Question: The tangent to the parabola y²=4ax at the point(a,2a) makes with x-axis an angle equal to
(a) π/3
(b) p/4
(c) p/2
(d) p/6 

Question: If the tangent at the point P(2,4) to the parabola y²= 8x +5 at Q and R then the mid-point of the QR is
(a) (2, 4)
(b) (4,2)
(c) (7, 9)
(d) None of these

Question: The normal at three points P, Q, R of the parabola y²= 4ax  meet in ( h,k). The centroid of ΔPQR lies on
(a) x = 0
(b) y = 0
(c) x =-a
(d) y=3 

Question: At what point on the parabola  y²=4x,  the normal makes equal angles with the coordinate axes?
(a) (4, 4)
(b) (9, 6)
(c) (4,-4)
(d) (1,-2) 

Question: The circle x²+ y² =5 meets the parabola y² = 4x at p and Q Then, the length P and Q is equal to
(a) 2
(b) 2 2
(c) 4
(d) None of these   

Question: The equation of latusrectum of a parabola is x+ y = 8 and the equation of the tangent at the vertex is x+ y = 12 , then length of the latusrectum is
(a) 4√ 2
(b) 2 √2
(c) 8
(d) 8 √2  

Question:

Question: The locus of the mid-point of the line segment joining the focus to a moving point on the parabola y²= 4ax is another parabola with the directrix
(a) x = − a
(b) x=–₂
(c) x = 0
(d) x = a/2 

Question: The equation (X-2)² + (Y-3)²=(3X+4Y-2/5)² represents
(a) a parabola
(b) a pair of straight lines
(c) an ellipse
(d) a hyperbola 

Question: The coordinates of a point on the parabola y²=8x whose focal distance is 4, is 
(a) (– 2, – 4), (2, – 4)
(b) (2, 4), (2, – 4)
(c) (1, 4), (2, – 4) (d)
(2, – 4), (– 2, 4) 

Question: If the equation of parabola is x² = -9y,  then equation of directrix and length of latusrectum are
(a) y = −9/4,8
(b) x =9/4,9
(c) y = 9/4,9 
(d) None of these 

Question: The length of the latusrectum of the parabola 169 {(x-1)² + (y-3)²} = (5x-12y +17)² is
(a) 14/13
(b) 12/13
(c) 28/13
(d) None of these

Question: If the area of an equilateral triangle inscribed in the circle, x² + y² + 10x + 12y + c = 0 is 27√3 sq. units then c is equal to:
(a) 13
(b) 20
(c) – 25
(d) 25

Question: Three circles of radii a, b, c (a < b < c) touch each other externally. If they have x-axis as a common tangent, then:
(a) 1/√a = 1/√b + 1/√c
(b) 1/√b = 1/√a + 1/√c
(c) a, b, c are in A.P
(d) √a, √b, √c are in A.P.

Question: The number of integral values of k for which the line, 3x + 4y = k intersects the circle, x² + y² – 2x – 4y + 4 = 0 at two distinct points is ________.

Question: If a line, y = mx + c is a tangent to the circle, (x – 3)² + y² = 1 and it is perpendicular to a line L₁, where L₁ is the tangent to the circle, x² + y² = 1 at the point (1/√2, 1/√2) ; then :
(a) c² – 7c + 6 = 0
(b) c² + 7c + 6 = 0
(c) c² + 6c + 7 = 0
(d) c² – 6c + 7 = 0

Question: A circle touching the x-axis at (3, 0) and making an intercept of length 8 on the y-axis passes through the point :
(a) (3, 10)
(b) (3, 5)
(c) (2, 3)
(d) (1, 5)

Question: The largest value of r for which the region represented by the set {ω ∈ C|ω – 4 – i| ≤r} is contained in the region represented by the set (z ∈c / | z -1|≤| z + i |), is equal to:
(a) (5/2)2
(b) 2√2
(c) (3/2)√2
(d) √17

Question: Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to
(a) 1/2
(b) 1/4
(c) √3/√2
(d) √3/2

Question: If the circles x² + y² + 5Kx + 2y + K = 0 and 2 (x² + y²) + 2Kx + 3y – 1= 0, (K∈R), intersect at the points P and Q, then the line 4x + 5y – K = 0 passes through P and Q, for:
(a) infinitely many values of K
(b) no value of K.
(c) exactly two values of K
(d) exactly one value of K

Question: Let C₁ and C₂ be the centres of the circles x² + y² – 2x –2y – 2 = 0 and x² + y² – 6x –6y + 14 = 0 respectively. If P and Q are the points of intersection of these circles then, the area (in sq. units) of the quadrilateral PC₁QC₂ is :
(a) 8
(b) 6
(c) 9
(d) 4

Question: If a variable line, 3x + 4y – λ = 0 is such that the two circles x² + y² – 2x – 2y + 1 = 0 and x² + y² – 18x – 2y + 78 = 0 are on its opposite sides, then the set of all values of λ is the interval :
(a) (2, 17)
(b) [13, 23]
(c) [12, 21]
(d) (23, 31)

Question: The line x = y touches a circle at the point (1, 1). If the circle also passes through the point (1, –3), then its radius is:
(a) 3
(b) 2√2
(c) 2
(d) 3√2

Question: If the length of the chord of the circle, x² + y² = r² (r > 0) along the line, y – 2x = 3 is r, then r2 is equal to :
(a) 9/5
(b) 12
(c) 24/5
(d) 12/5

Question: The circle passing through the intersection of the circles, x2 + y2 – 6x = 0 and x2 + y2 – 4y = 0, having its centre on the line, 2x -3y +12 = 0, also passes through the point:
(a) (–1, 3)
(b) (–3, 6)
(c) (–3, 1)
(d) (1, –3)

Question: If a tangent to the circle x² + y² = 1intersects the coordinate axes at distinct points P and Q, then the locus of the midpoint of PQ is:
(a) x² + y² – 4x²y² = 0
(b) x² + y² – 2xy = 0
(c) x² + y² – 16x²y² = 0
(d) x² + y² – 2x²y² = 0

Question: The equation Im [(iz − 2) / (z − i)] + 1 = 0, z ∈C, z ≠ i represents a part of a circle having radius equal to :
(a) 2
(b) 1
(c) 3/4
(d) 1/2

Question: A line drawn through the point P(4, 7) cuts the circle x² + y² = 9 at the points A and B. Then PA·PB is equal to :
(a) 53
(b) 56
(c) 74
(d) 65

Question: If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is :
(a) (x² + y²)² = 4R²x²y²
(b) (x² + y²)³ = 4R²x²y²
(c) (x² + y²)² = 4Rx²y²
(d) (x² + y²)² = 4R²xy

Question: A square is inscribed in the circle x² + y² – 6x + 8y -103 = 0 with its sides parallel to the coordinate axes. Then the distance of the vertex of this square which is nearest to the origin is :
(a) 6
(b) √137
(c) √41
(d) 13

Question: If one of the diameters of the circle, given by the equation, x² + y² – 4x + 6y – 12 = 0, is a chord of a circle S, whose centre is at (–3, 2), then the radius of S is:
(a) 5
(b) 10
(c) 5√2
(d) 5√3

Question: Equation of the tangent to the circle, at the point (1, –1) whose centre is the point of intersection of the straight lines x – y = 1 and 2x + y = 3 is :
(a) x + 4y + 3 = 0
(b) 3x – y – 4 = 0
(c) x – 3y – 4 = 0
(d) 4x + y – 3 = 0

Question: Two circles with equal radii are intersecting at the points (0, 1) and (0, –1). The tangent at the point (0, 1) to one of the circles passes through the centre of the other circle. Then the distance between the centres of these circles is :
(a) 1
(b) 2
(c) 2√2
(d) √2

Question: A circle touches the y-axis at the point (0, 4) and passes through the point (2, 0). Which of the following lines is not a tangent to this circle?
(a) 4x – 3y + 17 = 0
(b) 3x – 4y – 24 = 0
(c) 3x + 4y – 6 = 0
(d) 4x + 3y – 8 = 0

Question: If the curves, x² – 6x + y² + 8 = 0 and x² – 8y + y² + 16 – k = 0, (k > 0) touch each other at a point, then the largest value of k is ______.

Question: A circle cuts a chord of length 4a on the x-axis and passes through a point on the y-axis, distant 2b from the origin. Then the locus of the centre of this circle, is
(a) a hyperbola
(b) an ellipse
(c) a straight line
(d) a parabola

Question: If a circle passing through the point (–1, 0) touches y-axis at (0, 2), then the length of the chord of the circle along the x-axis is :
(a) 3/2
(b) 3
(c) 5/2
(d) 5

Question: Let the tangents drawn to the circle, x² + y² = 16 from the point P(0, h) meet the x-axis at point A and B. If the area of ΔAPB is minimum, then h is equal to :
(a) 4√2
(b) 3√3
(c) 3√2
(d) 4√3

Question: If a circle C passing through the point (4, 0) touches the circle x² + y² + 4x – 6y = 12 externally at the point (1, – 1), then the radius of C is:
(a) 2√5
(b) 4
(c) 5
(d) √57

Question: If the parabola y²=4ax passes through the point (3, 2) then the length of its latusrectum is
(a) 2/3
(b) 4/3
(c) 1/3
(d) 4 

Question: The equation y²-8y-x+19=0 represents

Question: The parametric coordinates of any point on the parabola y² = 4ax can be
(a) ( a-at²,-2at 
(b) (a− at²,2at)
(c) (a sin² t,-2a sin t) 
(d) (a sint,-2 a cot) 

Question: The length of the latusrectum of the parabola
169 {(x-1)² + (y-3)²} = (5x-12y+17)² is
(a) 14/13
(b) 12/13
(c) 28/13
(d) None of these 

Question: The latusrectum of the parabola y2=4ax  whose focal chord is PSQ such that SP = 3 and SQ = 2 , is given by
(a) 24/5
(b) 12/5
(c) 6/5
(d) 1/5 

Question: If a focal chord of the parabola y²=ax = is 2x-y-8=0,  then the equation of the directrix is
(a) x + = 4 0
(b) x − = 4 0
(c) y − = 4 0
(d) y + = 4 0 

Question: The parametric equation of a parabola is x = t²+1, y=2t+1.
The cartesian equation of its directrix is
(a) x = 0
(b) x + = 1 0
(c) y = 0
(d) None of the above

Question: The length of the chord of the parabola x² = 4y passing through the vertex and having slope cot α is
(a) 4 cos α α cosec² α
(b) 4 tan α α sec α
(c) 4 sin α  sec² α
(d) None of these 

Question: The line x −1 =0  is the directrix of the parabola
y²– kx + 8=0 
(a) 1/8
(b) 8
(c) 4
(d) 1/4 

Question: The position of the point (– 2, 2) with respect to the parabola y²-4y +9x+13 =0  is
(a) inside
(b) outside
(c) on
(d) None of these 

Question: The angle of intersection between the curves x² = 4(y+1) and x² = -4(y+1)  is
(a) π/6
(b) π/4
(c) 0
(d) π/2 

Question: The angle made by a double ordinate of length 8 a at the vertex of the parabola y²= 4ax  is
(a) π/3
(b) π/2
(c) π/4
(d) π/6 

Question: The equation of parabola having vertex (0, 0) passing through (2, 3) and axis is along x-axis is 
(a) x² = 9/2y 
(b) y² = 9/2 x 
(c) y² = – 9/2x 
(d) x² = -9/2 y

Question: Which one of the following points lies outside the ellipse (x²/ a²) + (y²/ b²) = 1 ?
(a) (a, 0)
(b) (0, b)
(c) (– a, 0)
(d) (a, b)

Question: The equation of the ellipse with focus at (± 5, 0) and x = 36/5 as one directrix is
(a) x²/36 + y²/25 = 1
(b) x²/36 + y²/11 = 1
(c) x²/25 + y²/11 = 1
(d) None of these

Question: Point (1, 2) relative to the circle x² + y² + 4x – 2y – 4 = 0 is a/an
(a) exterior point
(b) interior point, but not centre
(c) boundary point
(d) centre

Question: The value of λ does the line y = x + λ touches the ellipse 9x² + 16y² =144 is/are
(a) ± 2√2
(b) 2 ± √3
(c) ± 5
(d) 5 ± √2

Question: The equation of the circle, which touches the line y = 5 and passes through (–1, 2) and (1, 2) is
(a) 9x² + 9y² − 60y + 75 = 0
(b) 9x² + 9y² − 60x − 75 = 0
(c) 9x² + 9y² + 60y − 75 = 0
(d) 9x² + 9y² + 60x + 75 = 0

Question: Read the graph of the hyperbola. Match the column – I with column – II.

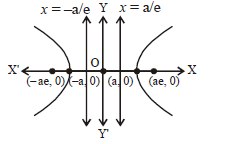
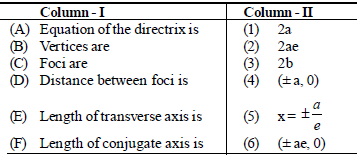
Codes
A B C D E F
(a) 5 6 4 2 3 1
(b) 4 5 2 6 3 1
(c) 5 4 6 2 1 3
(d) 5 4 2 6 3 1

Question: The foci of the ellipse x²/16 + y²/b² = 1 and the hyperbola x²/144 + y²/81= 1/25 coincide. Then the value of b² is
(a) 9
(b) 1
(c) 5
(d) 7

Question: If the circles x² + y² + 2ax + cy + a = 0 and x² + y² – 3ax + dy – 1 = 0 intersect in two distinct points P and Q then the line 5x + by – a = 0 passes through P and Q for
(a) exactly one value of a
(b) no value of a
(c) infinitely many values of a
(d) exactly two values of a

Question: If a circle passes through the point (a, b) and cuts the circle x² + y² = 4orthogonally, then the locus of its centre is
(a) 2ax – 2by – (a² + b² + 4) = 0
(b) 2ax + 2by – (a² + b² + 4) = 0
(c) 2ax – 2by + (a² + b² + 4) = 0
(d) 2ax + 2by + (a² + b² + 4) = 0

Question: If tangents are drawn to the ellipse x² + 2y² = 2 at all points on the ellipse other than its four vertices then the mid points of the tangents intercepted between the coordinate axes lie on the curve :
(a) 1/4x² + 1/2y² = 1
(b) x²/4 + y²/2 = 1
(c) 1/2x² + 1/4y² = 1
(d) x²/2 + y²/4 = 1

Question: Two sets A and B are as under :
A = {(a, b) ∈R × R : | a -5| <1 and | b – 5 | < 1};
B = {(a,b) ∈R × R : 4(a- 6)² + 9(b- 5)² ≤ 36}. Then :
(a) A ⊂ B
(b) A ∩ B = Φ (an empty set)
(c) neither A ⊂ B nor B ⊂ A
(d) B ⊂ A

Question: Which of the following points lies on the locus of the foot of perpendicular drawn upon any tangent to the ellipse, x²/4 + y²/2 = 1 from any of its foci?
(a) (-2, √3)
(b) (-1, √2)
(c) (-1, √3)
(d) (1, 2)

Question: If the normal at an end of a latus rectum of an ellipse passes through an extermity of the minor axis, then the eccentricity e of the ellipse satisfies:
(a) e⁴ + 2e² – 1 = 0
(b) e² + e – 1 = 0
(c) e⁴ + e2 – 1 = 0
(d) e² + 2e – 1 = 0

Question: If a circle of unit radius is divided into two parts by an arc of another circle subtending an angle 60° on the circumference of the first circle, then the radius of the arc is:
(a) √3
(b) 1/2
(c) 1
(d) √2

Question: If a circle C passing through (4, 0) touches the circle x2 + y² + 4x – 6y – 12 = 0 externally at a point (1, –1), then the radius of the circle C is :
(a) 5
(b) 2√5
(c) 4
(d) √57

Question: The eccentricity of an ellipse having centre at the origin, axes along the co-ordinate axes and passing through the points (4, –1) and (–2, 2) is :
(a) 1/2
(b) 2/√5
(c) √3/2
(d) √3/4

Question: Consider an ellipse, whose centre is at the origin and its ma or axis is along the x–axis. If its eccentricity is 3/5 and the distance between its foci is 6, then the area (in sq. units) of the quadrilateral inscribed in the ellipse, with the vertices as the vertices of the ellipse, is :
(a) 8
(b) 32
(c) 80
(d) 40

Question: The length of the semi-latus rectum of an ellipse is one third of its major axis, its eccentricity would be
(a) 2/3
(b) √2/3
(c) 1/√3
(d) 1/√2

Question: Equation of the ellipse whose axes are the axes of coordinates and which passes through the point (–3, 1) and has eccentricity √2/5/is
(a) 5x² + 3y² – 48 = 0
(b) 3x² + 5y² – 15 = 0
(c) 5x² + 3y² – 32 = 0
(d) 3x² + 5y² – 32 = 0

Question: If e₁ is the eccentricity of the ellipse x²/16 + y²/25 = 1 and e₂ is the eccentricity of the hyperbola passing through the foci of the ellipse and e₁e₂ = 1, then equation of the hyperbola is :
(a) x²/9 − y² /16 = 1
(b) x²/16 − y² /9 = 1
(c) x²/9 − y² /25 = 1
(d) x²/9 − y² /36 = 1

Question: If the eccentricity and length of latus rectum of a hyperbola are √13/3 and 10/3 units respectively, then what is the length of the transverse axis?
(a)7/2 unit
(b) 12 unit
(c) 15/2 unit
(d) 15/4 unit

Question: Length of the latus rectum of the ellipse x²/a² + y²/b² = 1 is
(a) b²/a²
(b) 2b/a
(c) 2b²/a
(d) 2a²/b

Question: The equation of the hyperbola whose vertices are (± 2, 0) and foci are (± 3, 0) is x²/a² – y²/b² = 1. Sum of a² and b² is
(a) 5
(b) 4
(c) 9
(d) 1

Question: A rod AB of length 15 cm rests in between two coordinate axes in such a way that the end point A lies on x-axis and end point B lies on y-axis. A point P(x, y) is taken on the rod in such a way that AP = 6 cm. Then, the locus of P is a/an.
(a) circle
(b) ellipse
(c) parabola
(d) hyperbola

Question: Two circles S₁ = x² + y² + 2g₁x + 2f₁y + c₁ = 0 and S₂ = x² + y² + 2g₂x + 2f₂y + c₂ = 0 cut each other orthogonally, then :
(a) 2g₁g₂ + 2f₁f₂ = c₁ + c₂
(b) 2g₁g₂ – 2f₁f₂ = c₁ + c₂
(c) 2g₁g₂ + 2f₁f₂ = c₁ – c₂
(d) 2g₁g₂ – 2f₁f₂ = c₁ – c₂

ASSERTION- REASON TYPE QUESTIONS

(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion:
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.

Question: Assertion : Eccentricity of conjugate hyperbola is equal to 

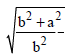
Reason : Equation of directrix of conjugate hyperbola is y = ±b/e

Question: Assertion : Centre of the circle x² + y² – 6x + 4y – 12 = 0 is (3, –2).
Reason : The coordinates of the centre of the circle x² + y² + 2gx + 2fy + c = 0 are (–1/2 coefficient of x, – 1/2 coefficient of y)

Question: Assertion : Latus rectum of a parabola is a line segment perpendicular to the axis of the parabola, through the focus and whose end points lie on the parabola.
Reason : The equation of a hyperbola with foci on the y-axis is : x²/a² − y²/b²= 1

Question: Assertion : Ellipse x²/25 + y²/16= 1 and 12x² – 4y² = 27 intersect each other at right angle.
Reason : Whenever focal conics intersect, they intersect each other orthogonally.

Question: Parabola is symmetric with respect to the axis of the parabola.
Assertion: If the equation has a term y² , then the axis of symmetry is along the x-axis.
Reason: If the eqution has a term x², then the axis of symmetry is along the x-axis.