Students should refer to Worksheets Class 11 Mathematics Complex Numbers and Quadratic Equations Chapter 5 provided below with important questions and answers. These important questions with solutions for Chapter 5 Complex Numbers and Quadratic Equations have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Complex Numbers and Quadratic Equations Worksheets Class 11 Mathematics
Question. Both the roots of given equation (x − a)(x − b) + (x − b)(x − c) + (x − c)(x − a) = 0 are always:
a. Positive
b. Negative
c. Real
d. Imaginary
Answer
C
Question. The solution of the equation x+1/x = 2
a. 2, –1
b. 0, –1, -1/5
c. -1 , 1/5
d. None of these
Answer
D
Question. For what values of k will the equation 2x − 2(1+ 3k)x + 7 (3 + 2k) = 0 have equal roots?
a. 1, –10/9
b. 2, –10/9
c. 3, –10/9
d. 4, –10/9
Answer
B
Question. The value of ‘a’ for which one root of the quadratic equation (a2 −5a + 3) x2 + (3a −1)x + 2 = 0 is twice as large as the other is:
a. 2/3
b. – 2/3
c. 1/3
d. – 1/3
Answer
A
Question. If the sum of the roots of the quadratic equation 0 ax2 + bx + c = is equal to the sum of the squares of their reciprocals, then a / c,b / a, c / b are in:
a. A.P.
b. G.P.
c. H.P.
d. None of these
Answer
C
Question. The value of x = √2+√2+√2+……..is:
a. –1
b. 1
c. 2
d. 3
Answer
C
Question. If α and β are the roots of 6x2 − 6x +1 = 0, then the value of
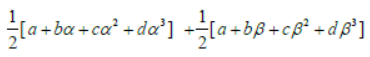
a. 1/4(a+b+c+d)
b. a/1 + b/2 + c/3 + d/4
c. a/2 – b/2 + c/3 – d/4
d. None of these
Answer
B
Question. If one root of a quadratic equation is 1/2+√5 ,then the equation is:
a. x2 + 4x + 1 = 0
b. x2 + 4x − 1 = 0
c. x2 − 4x + 1 = 0
d. None of these
Answer
B
Question. If one root of 5x2 +13x + k = 0 is reciprocal of the other, then k = ?
a. 0
b. 5
c. 1/6
d. 6
Answer
C
Question. Ifα,β are roots of x2 − 3x +1 = 0, then the equation whose roots are 1/α − 2 , 1/β − 2 is
a. x2 + x −1 = 0
b. x2 + x +1 = 0
c. x2 − x −1 = 0
d. None of these
Answer
C
Question. If one of the roots of the equation x2 + ax + b = 0 and x2 + bx + a = 0 is coincident. Then the numerical value of (a + b) is:
a. 0
b. – 1
c. 2
d. 5
Answer
D
Question. If x be real, then the minimum value of x2 − 8x +17 is:
a. 0– 1
b. 0
c. 1
d. 2
Answer
C
Question. The roots of the equation a(x2 +1) − (a2 +1)x = 0 are:
a. a,1/a
b. a, 2a
c. a,1/2a
d. None of these
Answer
A
Question. The roots of the equation ix2 − 4x − 4i = 0 are:
a. – 2i
b. 2i
c. –2i, –2i
d. 2i, 2i
Answer
C
Question. The number of roots of the quadratic equation 2 8sec θ − 6secθ +1 = 0 is:
a. Infinite
b. 1
c. 2
d. 0
Answer
D
Question. The number which exceeds its positive square root by 12 is:
a. 9
b. 16
c. 25
d. None of these
Answer
B
Question. If x2/3 − 7x +10 = 0, then x = ?
a. {125}
b. {8}
c. φ
d. {125, 8}
Answer
D
Question. If the sum of the roots of the equation λx2 – 2x + 3λ = 0 be equal to their product, then λ = ?
a. 4
b. −4
c. 6
d. None of these
Answer
D
Question. If the ratio of the roots of the equation ax2 + bx + c = 0 be p : q , then:
a. pqb2 + ( p + q) ac = 0
b. pqb2 − ( p + q) ac = 0
c. pqa2 − ( p + q) bc = 0
d. None of these
Answer
B
Question. The number of real roots of the equation esin esinx − e-sinx -4 = 0 are:
a. 1
b. 2
c. Infinite
d. None
Answer
D
Question. If
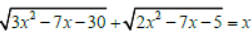
+ 5 ,then x is equal to:
a. 2
b. 3
c. 6
d. 5
Answer
C
Question. If α ,β are the roots of (x − a)(x − b) = c, c ≠ 0, then the roots of (x −α )(x −β ) + c = 0 shall be:
a. a, c
b. b,c
c. a,b
d. a + c,b + c
Answer
C
Question. If x1 , x2 , x3 are distinct roots of the equation ax2 + bx + c = 0 then:
a. a = b = 0,c∈R
b. a = c = 0,b∈R
c. 2 b − 4ac ≥ 0
d. a = b = c = 0
Answer
D
Question. If 3 is a root of x2 + kx – 24 = 0, it is also a root of :
a. 2 x + 5x + k = 0
b. 2 x − 5x + k = 0
c. 2 x − kx + 6 = 0
d. 2 x + kx + 24 = 0
Answer
C
Question. The equation ex − x −1 = 0 has:
a. Only one real root x = 0
b. At least two real roots
c. Exactly two real roots
d. Infinitely many real roots
Answer
A
Question. A real root of the equation log4 {log2(√x+8 -√x )} = 0 is:
a. 1
b. 2
c. 3
d. 4
Answer
A
Question. If the roots of the equations px2 + 2qx + r = 0 and qx2 – 2√prx+q = 0 be real, then:
a. p = q
b. q2 = pr
c. p2 = qr
d. r2 = pq
Answer
B
Question. Let α and β be the roots of the equation 2x + x +1 = 0 , the equation whose roots are α19, β7 is:
a. 2x − x − 1 = 0
b. 2x − x +1 = 0
c. 2x + x −1 = 0
d. 2x + x + 1 = 0
Answer
D
Question. If a > 0,b > 0,c > 0 then both the roots of the equation ax2 + bx + c = 0 ?
a. Are real and negative
b. Have negative real parts
c. Are rational numbers
d. None of these
Answer
B
Question. If the difference between the corresponding roots of x2+ ax + b = 0 and x2+ bx + a = 0 is same and a ≠ b, then:
a. a + b + 4 = 0
b. a + b − 4 = 0
c. a − b − 4 = 0
d. a − b + 4 = 0
Answer
A
Question. If the product of the roots of the equation (a +1)x2 + (2a + 3)x + (3a + 4) = 0 be 2, then the sum of roots is:
a. 1
b. –1
c. 2
d. –2
Answer
B
Question. If α ,β are the roots of the equation ax2 + bx + c = 0 then the equation whose roots are α+1/β and β+1/α is:
a. acx2 + (a + c)bx + (a + c)2 = 0
b. abx2 + (a + c)bx + (a + c)2 = 0
c. acx2 + (a + b)cx + (a + c)2 = 0
d. None of these
Answer
A
Question. If one root of the equation 2x + px + q = 0 is the square of the other, then:
a. p3 + q2 − q(3p +1) = 0
b. p3 + q2 + q(1+ 3p) = 0
c. p3 + q2 + q(3p −1) = 0
d. p3 + q2 + q(1− 3p) = 0
Answer
D
Question. If α and β be the roots of the equation 2x2 + 2(a+b)x + a2+b2 = 0,then the equation whose roots are (α + β)2 and (α −β)2 is:
a. x2 – 2abx – (a2-b2)2 = 0
b. x2 – 4abx + (a2-b2)2 = 0
c. x2 – 4abx – (a2-b2)2 = 0
d. None of these
Answer
B
Question. If α and β are the roots of the equation 2x2 − 3x + 4 = 0 , then the equation whose roots are α2 and β2 is:
a. 4x2 + 7x +16 = 0
b. 4x2 + 7x + 6 = 0
c. 4x2 + 7x +1 = 0
d. 4x2 − 7x +16 = 0
Answer
A
Question. If α ,β be the roots of the equation x2 − 2x + 3= 0, then the equation whose roots are 1/α2 and 1/β2 is:
a. x2 + 2x + 1 = 0
b. 9×2 + 2x + 1 = 0
c. 9×2 – 2x + 1 = 0
d. 9×2 + 2x −1= 0
Answer
B
Question. The solution set of the equation xlog(1-x)2 = 9 is
a. {– 2, 4}
b. {4}
c. {0, – 2, 4}
d. None of these
Answer
A
Question. If α ,β be the roots of x2 − px + q = 0 and α ′,β ′ be the roots of x2 − p’x + q’ = 0 then the value of (α −α ‘)2 + (β −α ′)2 + (a −β ′)2 + (β −β ′)2 is:
a. 2{p2 − 2q + p′ − 2q′ − pp′}
b. 2{p2 − 2q + p′ − 2q′ − qq′}
c. 2{p2 − 2q − p′ − 2q′ − pp′}
d. 2{p2 − 2q − p′ − 2q′ − qq′}
Answer
A
Question. If the roots of the equation x2 – 5x + 16 = 0 are α, β and the roots of equation x2 + px + q = 0 are α2 +β2 , αβ / 2 , then:
a. p = 1, q = −56
b. p = −1, q = −56
c. p = 1, q = 56
d. p = −1, q = 56
Answer
B
Question. If the roots of the equation 1/x+p + 1/x+q = 1/r are equal in magnitude but opposite in sign, then the product of the roots will be:
a. p2+q2/2
b. (p2+q2)/2
c. (p2-q2)/2
d. (p2-q2)/2
Answer
B
Question. If z = 1+i√3 /√3+i then (Z̅)100 lies in: C
a. I quadrant
b. II quadrant
c. III quadrant
d. IV quadrant
Answer
C
Question. If Xr = cos (π/2r) + sin (π/2r) then x1 . x2 .x3 …∞ is: C
a. –3
b. –2
c. –1
d. 0
Answer
C
Question. Let z1 and z2 be two distinct complex number and let z = (1–t) z1 = tz2 for some real number t with 0 < t < 1. If arg (w) denotes the principle argument of a non-zero complex number w, then: A,C,D
a. |z – z1| + |z – z2| = |z1 – z2|
b. arg (z–z1) = arg (z –z2)
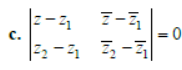
d. arg (z–z1) = arg (z2 – z1)
Answer
A,C,D
Question. If ω is the cube root of unity, then (3+5ω +3ω2)2 + (3+5ω +3ω2)2 ?
a. 4
b. 0
c. – 4
d. 5
Answer
C
Question. If i = −1 ,then
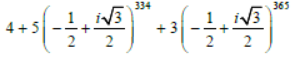
is equal to:
a. 1 − i√3
b. −1+i√3
c. i√3
d. − i√3
Answer
C
Question. If -1+√3 = reiθ then θ is equal to
a.π/3
b. -π/3
c. 2π/3
d. -2π/3
Answer
C
Question. Let ω is an imaginary cube root of unity then the value of
2(ω +1) (ω + 1) + 3(2ω +1) (2ω +1) + …..
2 +(n +1) (nω +1)(nω +1) is:

Answer
A
Question. If 1/x + x = 2cosθ , then xn + 1/xn is equal to
a. 2cos nθ
b. 2 sin nθ
c. cos nθ
d. sin nθ
Answer
A
Question. The roots of the equation x4 – 1 = 0, are:
a. 1, 1, i, – i
b. 1, –1, i, – i
c. 1, –1, ω, ω2
d. None of these
Answer
B
Question. If (1+i√3 )9 , + i = a + ib then b is equal to:
a. 1
b. 256
c. 0
d. 93
Answer
C
Question. The common roots of the equations z3+(1+i)z2 +(1+i) z +i = 0 (where i = √-1) and z1993 + z1994 + 1= 0 are:
a. 1
b. ω
c. ω2
d. ω981
Answer
B,C
Question. If x+1/x = √3, then x =?
a. cos Π/3 + isin Π/3
b. cos Π/2 + isin Π/2
c. sin Π/6 + icos Π/6
d. cos Π/6 + isin Π/6
Answer
D
Question. If α is a complex constant such that 2 α z + z +α = 0 has a real root, then:
a. α +α = 1
b. α +α = 0
c. α +α = −1
d. the absolute value of the real root is 1.
Answer
A,C,D
Question. i log (x-i/x+i) is equal to:
a. Π+2 tan-1x
b. Π–2 tan-1x
c. –Π+2 tan-1x
d. –Π–2 tan-1x
Answer
B
Question. If eiθ = cosiθ +i sinθ = + , then in %ABC value of eiA .eiB .eiC is:
a. – i
b. 1
c. –1
d. None of these
Answer
C
Read the following passage and answer the questions. Let S = S1∩S2 ∩S3 , where 1 S = {z∈C 😐 z |< 4},
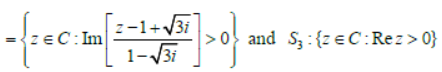
Question. Area of S is equal to:
a. 10π/3
b. 20π/3
c. 16π/3
d. 32π/3
Answer
B
Question. min |1 –3i –z | is equal to:
a. 2–√3/2
b. 2+√3/2
c. 3–√3/2
d. 3+√3/2
Answer
C
Question. Match the statements/expression given is Column-I with the values given in Column-II:


a. A→ 2; B→ 4; C→ 2; D→ 3
b. A→ 3; B→ 1; C→ 5; D→ 4
c. A→ 4; B→ 3; C→ 5; D→1
d. A→ 1; B→ 2; C→ 3; D→ 4
Answer
A
Question. Match the statements of Column I with these in Column II: [Note: Here z takes values in the complex plane and Im(z) and Re(z) denote respectively, the imaginary part and the real part of z]

a. A→ 2; B→ 1; C→ 5; D→ 3
b. A→ 1; B→ 2; C→ 3,5; D→1
c. A→ 4; B→ 2; C→ 3; D→ 2
d. A→ 1; B→ 2; C→ 3; D→ 4
Answer
A
Question. Let
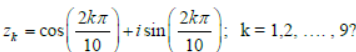

a. A→ 2; B→ 1, C→ 2; D→ 1
b. A→ 1; B→ 2; C→ 3; D→ 4
c. A→ 4; B→ 2; C→ 3; D→ 2
d. A→ 1; B→ 2; C→ 4; D→ 3
Answer
B
Question. If z is any complex number satisfying | z − 3 − 2i |≤ 2, then the maximum value of |2z – 6 + 5i|is:
Answer
3
Question. Let ω = eiπ/3 and a,b,c,x, y, z be non – zero complex numbers such that 2 a+b+c = x,+bω +cω 2 = y,a +bω +cω = z. Then, the value of
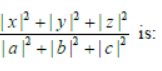
Answer
3
Question. If | z1 |= 2,| z2 |= 3,| z3 |= 4 and | 2z1 + 3z2 + 4z3 |= 9, then absolute value 8z2z3 +27z3z1 + 64z1z2 must be equal to:
Answer
216

