Students should refer to Worksheets Class 11 Mathematics Principle of Mathematical Induction Chapter 4 provided below with important questions and answers. These important questions with solutions for Chapter 4 Principle of Mathematical Induction have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Principle of Mathematical Induction Worksheets Class 11 Mathematics
Question. If the 4th term in the expansion of (px+x-1)m is 2.5 for all x∈R then:
(a) p = 5 / 2,m = 3
(b) p = 1/2, m= 6
(c) p = -1/2, m= 6
(d) None of these
Answer
B
Question. The coefficient of x32 in the expansion of (x4−1/x3)15 is
(a) 15C5
(b) 15C6
(c) 15C4
(d) 15C7
Answer
C
Question. Let R (5√5 + 11) 2n+1 and f = R − [R] where [.] denotes the greatest integer function. The value of R.f is:
(a) 42n+1
(b) 42n
(c) 42n–1
(d) 4-2n
Answer
A
Question. If in the expansion of (1 + x)m (1 − x)n , the coefficient of x and x2 are 3 and – 6 respectively, then m is:
(a) 6
(b) 9
(c) 12
(d) 24
Answer
C
Question. If T2/T3 in the expansion of (a + b)n and T3/T4 in the expansion of 3 (a+b) are equal, then n = ?
(a) 3
(b) 4
(c) 5
(d) 6
Answer
C
Question. The term independent of x in the expansion of (1+x)n (1+1/x)n is:
(a) C02 +2C12 +…..+(n+1)Cn2
(b) (C0 + C1+…….+Cn)2
(c) C02 +2C12 +…..+Cn2
(d) None of these
Answer
C
Question.
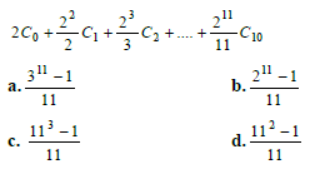
Answer
A
Question. The sum to (n +1) terms of the following series C0/2+C1/3+C2/4 +C3/5 +…..is
(a) 1/n+1
(b) 1/n+2
(c) 1/(n+1)
(d) None of these
Answer
D
Question. The coefficient of xn in the expansion of (1 + x) (1 – x)n is:
(a) 1 (-1)n−1
(b) (1)n(1-n)
(c) (-1)n-1(n-1)2
(d) (n −1)
Answer
B
Question. 6th term in expansion of (2x2–1/3x2)10 is:
(a) 4580/17
(b) –896/27
(c) 5580/17
(d) None of these
Answer
B
Question. If n is an integer greater than 1, then a−nC1(a-1)+nC2(a-2) +………+ (-1)n(a-n)=?
(a) a
(b)0
(c)a2
(d)2n
Answer
B
Question. If the sum of the coefficients in the expansion of (α2x2 − 2αx +1)51 vanishes, then the value of α is:
(a) 2
(b) –1
(c) 1
(d) – 2
Answer
C
Question. If the coefficients of rth term and (r + 4)th term are equal in the expansion of (1+ x)20 , then the value of r will be:
(a) 7
(b) 8
(c) 9
(d) 10
Answer
C
Question. If the expansion of (y2+C/y) the coefficient of y will be:
(a) 20c
(b)10c
(c) 10c3
(d) 20c2
Answer
C
Question.

(a) 2n/n+1
(b) 2n–1/n+1
(c) 2n+1–1/n+1
(d) None of these
Answer
C
Question. In the expansion of (x/2−3/x2)10 the coefficient of x4 is:
(a) 405/256
(b) 504/259
(c) 450/263
(d) None of these
Answer
A
Question. The term independent of x in the expansion of

(a) 3/2
(b) 5/4
(c) 5/2
(d) 2/3
Answer
B
Question. The coefficient of 7 x in the expansion of (x2/2−2/x)10 is:
(a) – 56
(b) 56
(c) – 14
(d) 14
Answer
C
Question. If coefficients of 2nd, 3rd and 4th terms in the binomial expansion of (1 + x)n are in (a)P., then n2 − 9n is equal to:
(a) – 7
(b) 7
(c) 14
(d) – 14
Answer
D
Question. The number of integral terms in the expansion of (√3 +3√5)256 is:
(a) 32
(b) 33
(c) 34
(d) 35
Answer
B
Question. The coefficient of x39 in the expansion of (x4−1/x3)15 is:
(a) – 455
(b) – 105
(c) 105
(d) 455
Answer
A
Question. Coefficient of xr in the expansion of (1–2x)-1/2 ?

Answer
B
Question. If x is so small that its two and higher power can be neglected and (1–2x)–1/2 (1–4x)–5/2 =1+ kx then k = ?
(a) 1
(b) –2
(c) 10
(d) 11
Answer
D
Question. The smallest positive integer n, for which n!(n+1/2)n hold is:
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. The fourth term in the expansion of (1–2x)3/2 will be:
Answer
B
Question. The expansion of 1/(4x–3x)1/2 binomial theorem will be valid, if:
a. x <1
b. | x |< 1
c. -2/√3 < x < 2/√3
d. None of these
Answer
D
Question. The value of c02 + 3c12 + 5c22 + …. to (n +1 terms (given that Cr ≡ nCr) is:

Answer
C
Question. The number of distinct terms in the expansion of (x + 2y − 3z + 5w− u)u is:
a. n+1
b. n+4C4
c. n+4Cn
d. (n+1)(n+2)(n+3)(n+4)/24
Answer
D
Question. Let 2 S(k) = 1+ 3+ 5 +…+ (2k −1) = 3+ k . Then which of the following is true:
(a) Principle of mathematical induction can be used to prove the formula
(b) S(k)⇒ S(k + 1)
(c) S(k)⇒/ S(k +1)
(d) S(1) is correct
Answer
C
Question. The expression
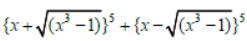
is a polynomial of degree:
a. 9C2
b. 7C8
c. 7
d. 8C1
Answer
B
Question. The coefficient of the middle term in the expansion of (1+x)2n is:
a. 2nCn
b. 1.3.5..(2n-1).2n/n!
c. 2⋅6…(4n − 2)
d. none of the above
Answer
A
Question. The approximate value of (7.995)1/3 correct to four decimal places is:
a.1.9995
b.1.9996
c.1.9990
d.1.9991
Answer
A
Question.

is equal to:
a. x
b. (1+x)1/3
c. (1−x)1/3
d. (1+x)-1/3
Answer
D
Question. The last digit of 334n + 1,n∈N is:
a. 4C3
b. 8C7
c. 8
d. 4
Answer
D
Paragraph
If m, n, r are positive integers and if r <m, r < n then
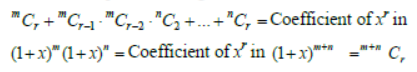
Answer
B
Question. The value of nC0 + nCn+nC1.nCn-1+…….+ nCn .nC0 is:
a. 2nCn-1
b. 2nCn
c. 2nCn+1
d. 2nC2
Answer
B
Question. The value of r for which 30Cr . 20Cr + 30Cr-1 . 20C1+….+30C0 . 20Cr is maximum, is:
a. 10
b. 15
c. 20
d. 25
Answer
D
Question. The value of r(0 ≤ r ≤ 30)for which 20Cr + 10Cr-1 . 20C0 + 20Cr-1 . 10C1 + ………..+ 20C0 . 10Cr is minimum, is:
a. 0
b. 1
c. 5
d. 15
Answer
A
Question. If Sn = nC0 + nC1+nC1.nC2 +……..+ nCn-1 .nCn and if Sn+1/Sn = 15/4. then n equals:
a. 2, 4
b. 4, 6
c. 6, 8
d. 8, 10
Answer
A
Question. If (1+x)n = C0+C1x+C2x2+…..+Cnxn and n is odd, then the value of C02–C12 = C22 –C32 +…….+ (-1)nCn2 is :
a. 0
b. 2nCn
c. c. (–1)n2nCn-1
d. d. 32nCn-2 d
Answer
A
Assertion and Reason
Note: Read the Assertion (A) and Reason (R) carefully to mark the correct option out of the options given below:
a. If both assertion and reason are true and the reason is the correct explanation of the assertion.
b. If both assertion and reason are true but reason is not the correct explanation of the assertion.
c. If assertion is true but reason is false.
d. If the assertion and reason both are false.
e. If assertion is false but reason is true.
Question. Assertion: Greatest term in the expansion of (√3+√2)50 is (50 20) 314211
Reason: Greatest term in the expansion (1+x)n ,x > 0 of is the rth term if (n+1)x/x+1 is not an integer and [(n+1)x/x+1 ] where [y] denotes the greatest integer ≤y.
Answer
D
Question. Let (1+x)n = C0 + C1x+C2x2+….Cnxn
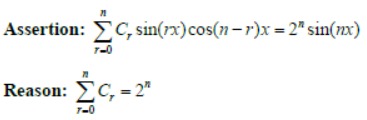
Answer
D
Question. Assertion: The coefficient of the term of independent of x in the expansion of
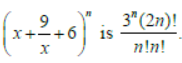
Reason: The coefficient of xr in the expansion of (1+x)n is (n r).
Answer
A
Question. Assertion: For any positive integers m, n (with n ≥ m),

Reason: Coefficient of xr in the expansion of (1+x)n is (n r).
Answer
D
Question. Let (1+x)n = C0 +C1x+C2x2+….+Cnxn.
Assertion: 5C02+7C12+9C22+…
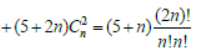
Reason: C02+C12+…+Cn2=2nCn
Answer
A
Match the Column
Question. Observe the following columns:


a. A→1, B→2→5, C→3-4
b. A→1, B→3-5, C→2-4
c. A→2, B→4-5, C→3-1
d. A→2, B→1-4, C→3-5
Answer
A
Question. Observe the following columns:

a. A→2-3, B→1-3-5, C→4
b. A→1-3, B→2-3-4, C→5
c. A→1-3, B→2-3-4, C→5
d. A→4-3, B→1-3-5, C→2
Answer
A
Question. Observe the following columns:


Answer
A
Question. The coefficient of x50 in the polynomials after parenthesis have been removed and like terms have been collected in the expansion.
(1+ x)1000 + x(1+ x)999 + x2(1+ x)998 is λ/μv! then the value of λ + 2μ+3v must be (v > μ ) ?
Answer
3954
Question. If (1+x)n = C0+C1x+C2x2+…….+Cnxn and
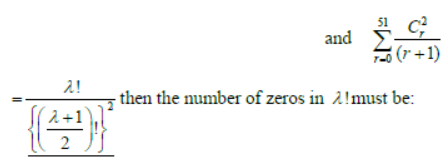
Answer
0024
Question. If
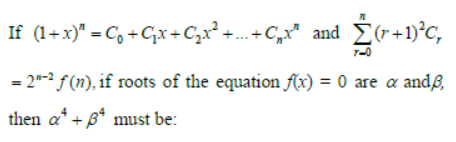
Answer
257