Students should refer to Worksheets Class 11 Mathematics Sequences and Series Chapter 9 provided below with important questions and answers. These important questions with solutions for Chapter 9 Sequences and Series have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Sequences and Series Worksheets Class 11 Mathematics
Question. The sum of 13 + 23 + 33+43 … +153 is:
a. 22000
b. 10000
c. 14400
d. 15000
Answer
C
Question. If the A.M., G.M. and H.M. between two positive numbers a and b are equal, then:
a. a = b
b. ab = 1
c. a > b
d. a < b
Answer
A
Question. If A1 , A2 ; G1 ,G2 and H1 ,H2 be two A.M.’s, G.M.’s and H.M.’s between two quantities, then the value of G1G2 /H1H2 is:

Answer
A
Question. If the sum of

to n terms is S, then S is equal to:
a. n(n+3)/4
b. n(n+2)/4
c. n(n+1)(n+2)/6
d. n2
Answer
A
Question. If the ratio of A.M. between two positive real numbers a and b to their H.M. is m : n, then a : b is:
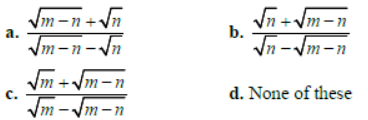
Answer
C
Question. If the A.M. of two numbers is greater than G.M. of the numbers by 2 and the ratio of the numbers is 4 : 1, then the numbers are:
a. 4, 1
b. 12, 3
c. 16, 4
d. None of these
Answer
C
Question. If | x |<1, then the sum of the series 1+ 2x + 3×2 + 4×3 +…∞ will be:
a. 1/1–x
b. 1/1+x
c. 1/(1+x)2
d. 1/(1–x)2
Answer
D
Question. If the ratio of H.M. and G.M. of two quantities is 12 : 13,then the ratio of the numbers is:
a. 1: 2
b. 2: 3
c. 3: 4
d. None of these
Answer
D
Question. The pth term Tp of HP is q(p+q) and qth term Tq is. p(p+q) when p >1,q >1, then: A,B,
a. Tp+q + pq =
b. Tpq = p + q
c. Tp+q > Tpq
d. Tpq > Tp+q
Answer
C
Question. If the arithmetic, geometric and harmonic means between two positive real numbers be A, G and H , then:
a. 2 A = GH
b. 2 H = AG
c. G = AH
d. 2 G = AH
Answer
D
Question. If xloga ,x logb , xlogc , x be in H.P., then a, b, c are in:
a. A.P.
b. H.P.
c. G.P.
d. None of these
Answer
C
Question. If A1, A2 are the two A.M.’s between two numbers a and b and G1 ,G2 be two G.M.’s between same two numbers, then A1+A2/G1.G2 ?
a. a+b/ab
b. a+b/2ab
c. 2ab/a+b
d. ab/a+b
Answer
A
Question. If G.M. = 18 and A.M. = 27, then H.M. is:
a. 1/18
b. 1/12
c.12
d. 9√6
Answer
C
Question. The sum to n terms of the series ………. . 22 + 42 + 62 + is:
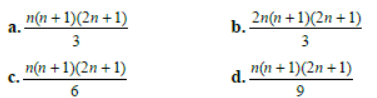
Answer
B
Question. If 9 A.M.’s and H.M.’s are inserted between the 2 and 3 and if the harmonic mean H is corresponding to arithmetic mean A , then A+6/H =?
a.1
b.3
c.5
d.6
Answer
C
Question. The sum of infinite terms of the following series

a. 3/16
b.35/8
c./354
d.35/16
Answer
D
Question. Sum of n terms of series 12 + 16 + 24 + 40 + ….. will be:
a. 2 (2n − 1) + 8n
b. 2(2n − 1) + 6n
c. 3(2n − 1) + 8n
d. 4(2n − 1) + 8n
Answer
D
Question. The sum of the series 1+1.3/6 + 1.3.5/6.8 + ….∞ is
a. 1
b. 0
c. ∞
d. 4
Answer
D
Question. If a, b, c, d are four positive numbers then:
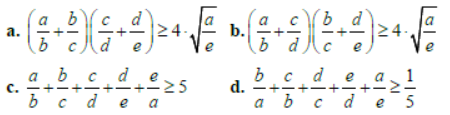
Answer
C
Question. If the first and (2n –1)th the term of an AP, a GP and a HP are equal and their nth terms are a, b and c respectively, then:
a. a = b = c
b. a + c = b
c. a ≥ b ≥ c
d. ac = b2
Answer
D
Question. The sum of the series 1+ 2x + 3×2 + 4×3 +……… upto n terms is:
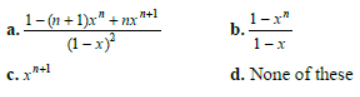
Answer
A
Question. If the set of natural numbers is partitioned into subsets S1 ={1},S2 = {2, 3},S3 = {4, 5, 6} and so on. Then the sum of the terms in 50 S is:
a. 62525
b. 25625
c. 62500
d. None of these
Answer
A
Question. The sum of (n + 1) terms of
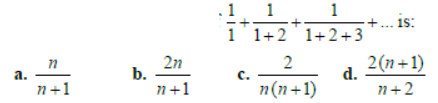
Answer
D
Question.
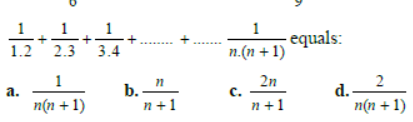
Answer
B
Question. Sum of the squares of first n natural numbers exceeds their sum by 330, then n = ?
a.8
b.10
c.15
d.20
Answer
B
Question. Let an be the nth term of the G.P. of positive numbers. Let
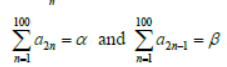
such that α ≠ β, then the common ratio is:
a. α/β
b. β/α
c. α/β
d. β/α
Answer
A
Question. If x = log 3+ log7 5 + log9 7 then:
a. x≥3/2
b. x≥1/3√2
c. x≥3/3√2
d. 1/√3
Answer
C
Question.
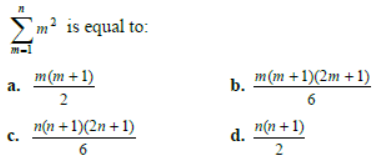
Answer
C
Question. First term of the 11th group in the following groups (1), (2, 3, 4), (5, 6, 7, 8, 9),……….is:
a.89
b. 97
c.101
d.123
Answer
C
Question. For a positive integer n let an =
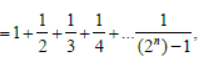
a. a (100) ≤ 100
b. a (100) >100
c. a (200) ≤ 100
d. a (200) > 100
Answer
A,D
Question. The third term of a geometric progression is 4. The product of the first five terms is :
a. 43
b. 45
c. 44
d. 47
Answer
B
Question. The H. M between roots of the equation x2 – 10x + 11 = 0 is equal to :
a. 1/5
b. 5/21
c. 21/20
d. 11/5
Answer
D
Question. For a, b, c to be in G.P. What should be the value of a − b/b − c ?
a. ab
b. bc
c. a/b or b/c
d. None of these
Answer
C
Question. If a, b, c are in geometric progression and a, 2b, 3c are in arithmetic progression, then what is the common ratio r such that 0 < r < 1 ?
a. 1/3
b. 1/2
c. 1/4
d. 1/8
Answer
A
Question. In a Geometric Progression with first term a and common ratio r, what is the Arithmetic Mean of the first five terms?
a. a + 2r
b. a r2
c. a r5 – 1./[5r – 1.]
d. a r4 – 1./[5r – 1.]
Answer
C
Question. Which term of the following sequence 1/3 , 1/9 , 1/27 …….is 1/19683 ?
a. 3
b. 9
c. 6
d. None of these
Answer
B
Question. The value of 3 –1 + 1/3 – 1/9 + …….. + is equal to:
a. 20/9
b. 9/20
c. 9/4
d. 4/9
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
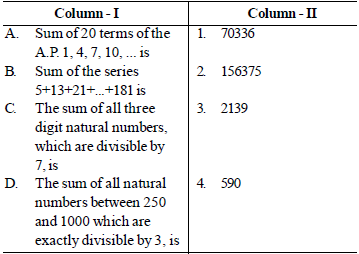
Codes
A B C D
a. 4 3 1 2
b. 4 1 3 2
c. 2 3 1 4
d. 2 1 3 4
Answer
A
Question. The following consecutive terms 1/1+ √x, 1/1− x, 1/1− x of a series are in:
a. H.P.
b. G.P.
c. A.P.
d. A.P., G.P.
Answer
C
Question. How many terms of G.P. 3, 32, 33, ………. are needed to give the sum 120?
a. 3
b. 4
c. 5
d. 6
Answer
B
STATEMENT TYPE QUESTIONS
Question. Statement I: If ‘a’ is the first term and ‘d’ is the common difference of an A.P., then its nth term is given by an = a – n – 1.d
Statement II: The sum Sn of n terms of an A.P. with first term ‘a’ and common difference ‘d’ is given by Sn = n/2 {2a + n – 1.d}
Choose the correct option.
a. Only I is true
b. Only II is true
c. Both are true
d. Both are false
Answer
B
Question. I. 11th terms of the G.P. 5, 10, 20, 40, … is 5120
II. If A.M. and G.M. of roots of a quadratic equation are 8 and 5, respectively, then obtained quadratic equation is x2 – 16x + 25 = 0
Choose the correct option.
a. Only I is true
b. Only II is true.
c. Both are true
d. Both are false.
Answer
C
Question. Consider the following statements.
I. The nth term of a G.P. with first term ‘a’ and common ratio ‘r’ is given by an = a.rn–1.
II. Geometric mean of a and b is given by ab.1/3
Choose the correct option.
a. Only I is true
b. Only II is true
c. Both are true
d. Both are false
Answer
A
Question. Consider the following statements
I. If a1, a2, …, an … is a sequence, then the expression a1 + a2 + … + an +… is called a series.
II. Those sequences whose terms follow certain patterns are called progressions.
Choose the correct option.
a. Only I is false
b. Only II is false
c. Both are false
d. Both are true
Answer
D
Question. I. If each term of a G.P. be raised to the same power, the resulting sequence also forms a G.P.
II. 25th term of the sequence 4, 9, 14, 19, … is 124.
Choose the correct option.
a. Both are true
b. Both are false
c. Only I is true
d. Only II is true
Answer
A
