Students should refer to Worksheets Class 12 Mathematics Relations and Functions Chapter 1 provided below with important questions and answers. These important questions with solutions for Chapter 1 Relations and Functions have been prepared by expert teachers for Class 12 Mathematics based on the expected pattern of questions in the class 12 exams. We have provided Worksheets for Class 12 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Relations and Functions Worksheets Class 12 Mathematics
Question. If X = {8n – 7 – 1: n ∈ N): n∈N} and Y = {49(n–1): n∈N} then:
(a) X ⊆ Y
(b) Y ⊆ X
(c) X = Y
(d) None of these
Answer
A
Question: Let f :R→ R be defined by f (x)= x/√1+x2,then (fofof) (x) is
(a) x/√1+x2
(b) x/√1+3x2
(c) x
(d) 1
Answer
B
Question: Let f, g: R→ R be two functions defined as f (x)= |x |+ x and g (x)= |x |-x, ∀ x∈ R.Then, fog and gof are respectively.

Answer
A
Question: If f (x)={4-(x-7)3},then f-1 (x) is
(a) 7+ (4-x)1/3
(b) 7+ (4-x)3
(c) 7+ (x-4)1/3
(d) 7+(x-4)3
Answer
A
Question: If f (x)=(4x+3)/(6x-4),x≠2/3,then the value of (fof) (x) is, for all x ≠2/3
(a) 1/x
(b) x2
(c) x
(d) 1/x2
Answer
C
Question: Let f : x →y be an invertible function, then f has
(a) unique inverse
(b) not a unique inverse
(c) only two inverse
(d) None of these
Answer
A
Question: Let f :{1,3,4 } → {1,2,5} and g :{1,2,5}→ {1,3} be given by f :{ (1,2 ), ( 3,5), (4,1)} and g :{( 1,3), (2,3), ( 5,1)} then gof is
(a) {(3,1 ), (1,3), (3,4)}
(b) {(1,3 ), ( 3,1), (4,3)}
(c) {(1,1), (2,2), ( 4,4)}
(d) None of the above
Answer
B
Question: Let A ={−1,0,1,2}, B = {−4,-2,0,2} and f,g: A→ B be the function defined by f (x)= x2−x,x ∈ A A and g (x)=2////-1,x ∈ A ,then f and g
(a) does not exist
(b) are not equal
(c) are equal
(d) None of these
Answer
A
Question: Let f R→ R: be the Signum function defined as

greatest integer function given by g(x)= [x] is greatest integer less than or equal to x. Then, fog and gof do not coincide in
(a) (0,1)
(b) [0,1]
(c) [0,1)
(d) (0,1]
Answer
D
Question:
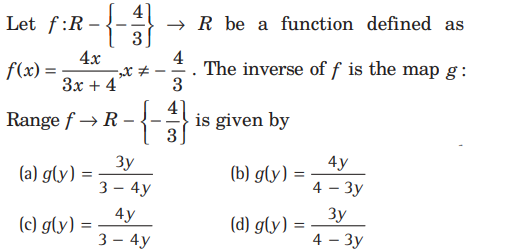
Answer
B
Question: If f(x)=ax+a-x/2 and f(x+y)+ f(x- y)=kf (x) f(y),then k is equal to
(a) 2
(b) 4
(c) –2
(d) None of these
Answer
A
Question:
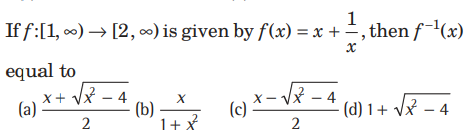
Answer
A
Question:

Answer
D
Question: Which of the following cannot have their inverse defined?
(a) f:[-π/2,π/2]→ [−1,1] defined by y= sin3 x
(b) f: R→ R+ defined by y ex
(c) f: R+→ R defined by y = log |x|
(d) f: R → R+ defined by y= e |x|
Answer
D
Question: If f:[π/2,3π/2] → [−1,1] is defined by f(x) =sin x, then f-1 (x) is given by
(a) sin −1x
(b) π +sin -1
(c) π − sin-1x
(d) None of these
Answer
C
Question:

Answer
D
Question: If the function f:[1,∞) → [1,∞) is defined by f (x=2x(x-1),then f-1 (x)is equal to
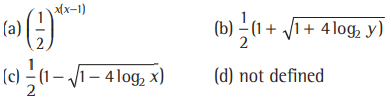
Answer
B
Question: If f (x)= lx+m and f (x+2)- f (x) =2, then
(a) l =1,m = 0
(b) l =0,m=1
(c) l =0,m=0
(d) l =1,m ∈ R
Answer
D
Question: If f (x)= cos (log x), then
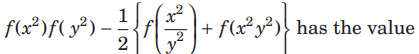
(a) −2
(b) −1
(c) 1/2
(d) None of these
Answer
D
Question: If f (x+ y, x-y)=x y, then f ( x, y) is equal to
(a) x y
(b) x2– y2
(c) x2 -y2
(d) x +y
Answer
C
Question: The function f (x)= log =(1+x/1-x) satisfies the equation
(a) f(x+2)- 2f(x+1)+ f(x)=0 )
(b) f(x+1)+ f(x) = f(x[x+1)]
(c) f (x1)⋅f(x2) = f(x1+x2)
(d) f (x1)⋅f(x2) = f(x1+x2/1+x1x2)
Answer
B
Question: If af (x)+bf(1/x)=x+5/x, (a≠b), then f(x) is equal to

Answer
C
Question: Two functions f and g are said to commute if ( fog)(x)= ( gof)(x), for all x, which of the following function are commute?
Answer
C
Question: Let g( x)=1+x-[x] and f(x)=
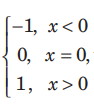
then for all x f[g(x) is equal to
(a) x
(b) 1
(c) f (x)
(d) g (x)
Answer
B
Question: If f (x)=x-1/x+1,then f(2x) is equal to
(a) f (x)+1/f(x)+3
(b) 3f(x)+1/f(x)+3
(c) f(x)+3/f(x)+1
(d) f(x)+3/3f(x)+1
Answer
B
Question. Let A = [x : x ∈ R, |x| < 1] B = [x : x ∈ R, |x – 1| ≥ 1] and A ∪ B = R − D, then the set D is:
(a) [x : 1 < x ≤ 2]
(b) [x : 1 ≤ x < 2]
(c) [x : 1 ≤ x ≤ 2]
(d) None of these
Answer
B
Question. If the sets A and B are defined as A = {(x, y) : y =1/x,0≠∈x R}= B = {(x, y) : y = −x, x ∈ R} , then:
(a) A ∩B = A
(b) A ∩ B = B
(c) A ∩ B =φ
(d) None of these
Answer
C
Question. Given the sets A = {1, 2, 3}, B = {3, 4} , C = {4, 5, 6}, then: A ∪ (B ∩ C) is
(a) {3}
(b) {1, 2, 3, 4}
(c) {1, 2, 4, 5}
(d) {1, 2, 3, 4, 5, 6}
Answer
B
Question. If A and B are any two sets, then A ∪ (A ∩ B) is equal to:
(a) A
(b) B
(c) c A
(d) c B
Answer
A
Question. If the set A has p elements, B has q elements, then the number of elements in A × B is:
(a) p + q
(b) p + q + 1
(c) pq
(d) p2
Answer
C
Question. If the sets A and B are defined as:
{( , ) : , } x A = x y y = e x∈R
B = {(x, y) : y = x, x∈ R}, then
(a) B ⊆ A
(b) A ⊆ B
(c) A ∩ B =φ
(d) A ∪ B = A
Answer
C
Question. If A,B and C are any three sets, then A×(B∩C) is equal to:
(a) (A × B) ∪ (A × C)
(b) (A × B) ∩ (A × C)
(c) (A ∪ B) × (A ∪ C)
(d) (A ∩ B) × (A ∩ C)
Answer
B
Question. Let 2 2 P = {(x, y) | x + y = 1, x, y∈R} .Then P is:
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Anti-symmetric
Answer
B
Question. If X = {4n – 3n – 1 : n ∈ N} and Y ={9(n – 1) : n ∈ N} then X ∪Y is equal to:
(a) X
(b) Y
(c) N
(d) None of these
Answer
B
Question. Let R and S be two non-void relations on a set (A) Which of the following statements is false:
(a) R and S are transitive ⇒ R ∪ S is transitive
(b) R and S are transitive ⇒ R ∩ S is transitive
(c) R and S are symmetric ⇒ R ∪ S is symmetric
(d) R and S are reflexive ⇒ R ∩ S is reflexive
Answer
A
Question. In a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C If 2% families buy all the three newspapers, then number of families which buy: A only is
(a) 3100
(b) 3300
(c) 2900
(d) 1400
Answer
B
Question. Which of the following is the empty set?
(a) {x : x is a real number and 2 x −1 = 0}
(b) {x : x is a real number and 2 x +1 = 0}
(c) {x : x is a real number and 2 x − 9 = 0}
(d) {x : x is a real number and 2 x = x + 2}
Answer
B
Question. In a city 20 percent of the population travels by car, 50 percent travels by bus and 10 percent travels by both car and bus. Then persons travelling by car or bus is:
(a) 80 percent
(b) 40 percent
(c) 60 percent
(d) 70 percent
Answer
C
Question. Let X = {1, 2, 3, 4,5} and Y = {1, 3,5, 7, 9} . Which of the following is/are relations from X to Y?
(a) 1 R = {(x, y) | y = 2 + x, x∈ X, y∈Y}
(b) 2 R = {(1,1), (2,1), (3, 3), (4, 3), (5, 5)}
(c) 3 R = {(1,1), (1, 3)(3, 5), (3, 7), (5, 7)}
(d) 4 R = {(1, 3), (2, 5), (2, 4), (7, 9)}
Answer
A,B,C
Question. In a class of 55 students, the number of students studying different subjects are 23 in mathematics, 24 in physics, 19 in chemistry, 12 in mathematics and physics, 9 in mathematics and chemistry, 7 in physics and chemistry and 4 in all the three subjects. The number of students who have taken exactly one subject is:
(a) 6
(b) 9
(c) 7
(d) 5
Laws of Algebra of Sets
Answer
D
Question. If A = {2, 4, 5}, B = {7, 8, 9}, then n(A× B) is equal to:
(a) 6
(b) 9
(c) 3
(d) 0
Answer
B
Question. If A ⊆ B , then A ∪ B is equal to:
(a) A
(b) B ∩ A
(c) B
(d) None of these
Answer
C
Question. If P, Q and R are subsets of a set A, then R×(Pc∪Qc)c =?
(a) (R × P) ∩ (R × Q)
(b) (R × Q)∩(R × P)
(c) (R × P)∪(R × Q)
(d) None of these
Answer
B
Question. The set of intelligent students in a class is:
(a) A null set
(b) A singleton set
(c) A finite set
(d) Not a well defined collection
Answer
D
Question. Let A = {1, 2, 3}. The total number of distinct relations that can be defined over A is:
(a) 9 2
(b) 6
(c) 8
(d) 5
Answer
A
41. Domain of definition of the function (Image 15)
Answer
C
Question. If f ( y) = log y, then f ( y) + f(1/y) is equal to:
(a) 2
(b) 1
(c) 0
(d) –1
Answer
C
Question. Function f : N → N, f (x) = 2x + 3 is:
(a) One-one onto
(b) One-one into
(c) 0 Many-one onto
(d) Many –one into
Answer
B
Question. Domain of the function 1/√x2-1 is:
(a) (−∞, − 1)∪ (1,∞)
(b) (−∞, − 1]∪(1,∞)
(c) (−∞, − 1)∪ [1,∞)
(d) None of these
Answer
A
Question. The relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on set A = {1, 2, 3} is:
(a) Reflexive but not symmetric
(b) Reflexive but not transitive
(c) Symmetric and Transitive
(d) Neither symmetric nor transitive
Answer
A
Question. With reference to a universal set, the inclusion of a subset in another, is relation, which is?
(a) Symmetric only
(b) Equivalence relation
(c) Reflexive only
(d) None of these
Answer
D
Question. Let X be a family of sets and R be a relation on X defined by ‘A is disjoint from B’. Then R is:
(a) Reflexive
(b) Symmetric
(c) Anti-symmetric
(d) Transitive
Answer
B
Question. If A,B and C are non-empty sets, then (A–B) ∪ (B – A) equals?
(a) (A ∪ B) – B
(b) A – (A ∩ B)
(c) (A ∪ B) – (A ∩ B)
(d) (A ∩ B) ∪ (A ∪ B)
Answer
C
Question. The solution set of 8 x ≡ 6(mod 14), x ∈ Z , are:
(a) [8] ∪ [6]
(b) [8] ∪ [14]
(c) [6] ∪ [13]
(d) [8] ∪ [6] ∪ [13]
Answer
C
Question. The function f : R → R defined by f (x) = (x −1)(x − 2)(x − 3) is:
(a) One-one but not onto
(b) Onto but not one-one
(c) Both one-one and onto
(d) Neither one-one nor onto
Answer
B
Question. If R be a relation < from A = {1,2, 3, 4} to B = {1, 3, 5}
i.e., (a, b)∈R⇔a < b, then −1 RoR is:
(a) {(1, 3), (1, 5), (2, 3), (2, 5), (3, 5), (4, 5)}
(b) {(3, 1) (5, 1), (3, 2), (5, 2), (5, 3), (5, 4)}
(c) {(3, 3), (3, 5), (5, 3), (5, 5)}
(d) {(3, 3) (3, 4), (4, 5)}
Answer
C
Question. The function f : R → R defined by x f(x) = ex is:
(a) Onto
(b) Many-one
(c) One-one and into
(d) Many one and onto
Answer
C
Question. If A contains 10 elements then total number of functions defined from A to A is:
(a) 10
(b) 210
(c) 1010
(d) 210 –
Answer
C
Question. The domain of the function f(x) = 1/√|x|-x is:
(a) R+
(b) R−
(c) R0
(d) R
Answer
B
Question. Let A = {1, 2, 3}, B = {1, 3, 5}. A relation R : A → B is defined by R = {(1, 3), (1, 5), (2, 1)}. Then −1 R is defined by:
(a) {(1,2), (3,1), (1,3), (1,5)}
(b) {(1, 2), (3, 1), (2, 1)}
(c) {(1, 2), (5, 1), (3, 1)
(d) None of these
Answer
C
Question. The domain of the function f (x) = √x-x2 + √(4 + x) + √(4 − x) is:
(a) [−4,∞)
(b) [−4, 4]
(c) [0, 4]
(d) [0,1]
Answer
D
Question. Suppose A1 , A2 , A3 ,…….., A30 are thirty sets each having 5 elements and B1, B2 , ……., Bn are n sets each with 3 elements. (Image13) and each elements of S belongs to exactly 10 of the Ais ‘ and exactly 9 of the Bjs’ .Then n is equal to:
(a) 15
(b) 3
(c) 45
(d) None of these
Answer
C
Question. The domain of the function √log(x2-6x+6) is:
(a) (−∞,∞)
(b) (−∞,3− √3)∪(3+ √3,∞)
(c) (−∞,1]∪[5,∞)
(d) (−∞,1]∪[3,∞)
Answer
C
Question. Let R be a relation on the set N of natural numbers defined by nRm ⇔ n is a factor of m (i.e., n|m). Then R is:
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric
Answer
D
Question. The domain of the derivative of the function (Image 15)
(a) R −{0}
(b) R −{1}
(c) R −{−1}
(d) R −{−1, 1}
Answer
C
Question. Range of the function f(x) = x2+x+2 /x2+x+1 ; x ∈ R is:
(a) (1,∞)
(b) (1,11/ 7)
(c) (1, 7 / 3]
(d) (1, 7 / 5]
Answer
C
46. Which of the following is an even function? (Image 15)
Answer
A
47. Which of the following is an even function? (Image 15)
Answer
B
Question. The period of the function f(x)=2cos 1/3 (x-Π) is:
(a) 6π
(b) 4π
(c) 2π
(d) π
Answer
A
Question. Given two finite sets A and B such that n(A) = 2, n(B) = 3.
Then total number of relations from A to B is?
(a) 4
(b)8
(c) 64
(d) 9
Answer
C
Question. The domain of the function 3 ( ) log x f x + = 2 (x −1) is:
(a) (−3, − 1)∪(1,∞)
(b) [−3, − 1)∪[1,∞)
(c) (−3,−2)∪(−2, − 1) ∪(1,∞)
(d) [−3, − 2)∪(−2, − 1)∪[1,∞]
Answer
C
Question. The period of | sin 2x | is:
a. π/4
b. π/2
c. π
d. 2π
Answer
B
