Students should refer to Worksheets Class 11 Mathematics Trigonometric Functions Chapter 3 provided below with important questions and answers. These important questions with solutions for Chapter 3 Trigonometric Functions have been prepared by expert teachers for Class 11 Mathematics based on the expected pattern of questions in the class 11 exams. We have provided Worksheets for Class 11 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Trigonometric Functions Worksheets Class 11 Mathematics
Question. If cos θ = –3/5 and π < θ < 3π/2, then the value of (cosecθ + cotθ/secθ – tanθ) is equal to 1/m . Value of m is
(a) 2
(b) 4
(c) 5
(d) 6
Answer
D
Question. If cos θ = –3/5 and π < θ < 3π/2 , then the value of (cosecθ + cotθ / secθ – tanθ) is equal to
(a) 1/3
(b) 2/3
(c) 13/2
(d) None of these
Answer
D
Question. Match the following in column-I with the given in column-II.
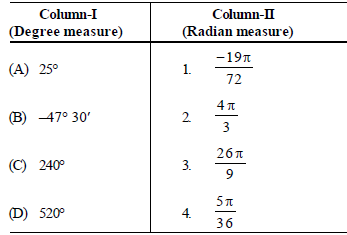
Codes:
A B C D
(a) 4 2 1 3
(b) 3 1 2 4
(c) 4 1 2 3
(d) 3 2 1 4
Answer
C
Question. The value of 4 sin α sin(α + π/3) sin(α + 2π/3) =
(a) sin 3α
(b) sin 2α
(c) sin α
(d) sin2 α
Answer
A
Question. If tan θ = 1/√7 , then (cosec2θ – sec2θ/cosec2θ + sec2θ is equal to m/m+1. The value of m is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question. The value of sin(–11π/3) is √3/m . Value of ‘m’ is
(a) 1
(b) 2
(c) 3
(d) 5
Answer
B
Question. General solution of the equation tan θ tan 2θ = 1 is given by
(a) (2n + 1)π/4 ,n ∈ I
(b) nπ + π/6, n ∈ I
(c) nπ – π/6, n ∈ I
(d) nπ ± π/6, n ∈ I
Answer
D
Question. The solution of the equation [sin x + cos x]1 + sin 2x = 2, –π ≤ x ≤ π is
(a) π/2
(b) π
(c) π/4
(d) 3π/4
Answer
C
Question. Match the following in column-I with the given in column-II.
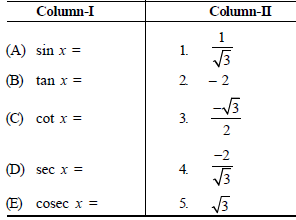
Codes:
A B C D E
(a) 3 5 1 2 4
(b) 1 5 3 2 4
(c) 3 5 1 4 2
(d) 3 1 5 4 2
Answer
A
Question. cos (3π/4+x) – cos (3π/4 –x) is equal to
(a) √2 sin x
(b) –2 sin x
(c) – √2 sin x
(d) None of these
Answer
C
Question. If sin 2θ + sin 2Φ = 1/2, cos 2θ + cos 2Φ = 3/2, then value of cos2 (θ – Φ) is
(a) 5/8
(b) 3/8
(c) –5/8
(d) 3/5
Answer
A
Question. If sin 3α = 4 sin α sin (x + α ) sin (x – α ), then x =
(a) nπ ± π/6
(b) nπ ± π/3
(c) nπ ± π/4
(d) nπ ± π/2
Answer
B
Question. sin x – sin 3x / sin2 x –cos2 x is equal to
(a) sin 2x
(b) cos 2x
(c) tan 2x
(d) None of these
Answer
D
Question. If sin A = 3/5 , 0 < A < π/2 and cos B = –12/13, π < B < 3π/2 , then value of sin (A – B) is
(a) –13/82
(b) –15/65
(c) –13/75
(d) –16/65
Answer
D
Question. If tan θ = –4/3 ,then sin θ is
(a) –4/5 but not 4/5
(b) –4/5 or 4/5
(c) 4/5 but not –4/5
(d) None of these
Answer
B
Question. If A + B = 45°, then (cot A – 1) (cot B – 1) is equal to
(a) 1
(b) 1/2
(c) –1
(d) 2
Answer
D
Question. Number of solutions of the equation tan x + sec x = 2 cos x lying in the interval [0, π] is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
C
Question. If n is any integer, then the general solution of the equation cos x – sin x = 1/√2 is
(a) x = 2nπ – π/12 or x = 2nπ + 7π/12
(b) x = nπ ± π/12
(c) x = 2nπ + π/12 or x = 2nπ – 7π/12
(d) x = nπ + π/12 or x = nπ – 7π/12
Answer
C
Question. If 5 tan θ = 4, then 5 sinθ – 3 cosθ /5 sinθ + 2 cosθ =
(a) 0
(b) 1
(c) 1/6
(d) 6
Answer
C
Question. If tan θ = 3 and θ lies in IIIrd quadrant, then the value of sin θ is
(a) 1/√10
(b) 2/√10
(c) –3/√10
(d) –5/√10
Answer
C
Question. If 2 tan2 θ = sec2θ, then general value of θ are
(a) nπ ± π/4 , n ∈ I
(b) nπ ± π/6 , n ∈ I
(c) 2nπ + π/4 , n ∈ I
(d) 2nπ ± π/6 , n ∈ I
Answer
A
Question. The angle in radian through which a pendulum swings and its length is 75 cm and tip describes an arc of length 21 cm, is
(a) 7/25
(b) 6/25
(c) 8/25
(d) 3/25
Answer
A
Question. Match the following in column-I with the given in column-II.

Codes:
A B C D
(a) 1 4 3 2
(b) 2 4 1 3
(c) 2 1 4 3
(d) 3 1 4 2
Answer
C
Question. What is the value of radian measures corresponding to the 25° measures ?
(a) 5π/36
(b) 2π/36
(c) 3π/36
(d) 4π/36
Answer
A
Question. If cos 7θ = cos θ – sin 4θ, then the general value of θ is
(a) nπ/4, nπ/3 + π/18
(b) nπ/3, nπ/3 + (–1)nπ/18
(c) nπ/4, nπ/3 + (–1)nπ/18
(d) nπ/6, nπ/3 + (–1)nπ/18
Answer
C
Question. Number of solutions of equation, sin 5x cos 3x = sin 6x cos 2x, in the interval [0, π] is
(a) 4
(b) 2
(c) 3
(d) 5
Answer
D
Question. sin 12° sin 24° sin 48° sin 84° =
(a) cos 20° cos 40° cos 60° cos 80°
(b) sin 20° sin 40° sin 60° sin 80°
(c) 3/15
(d) None of these
Answer
A
Question. If x + 1/x = 2 cos θ , then x3 + 1/x3 is:
(a) 1/2 cos 3θ
(b) 2 cos 3θ
(c) cos 3θ
(d) 1/3 cos 3θ
Answer
B
Question. Value of cot 5° cot 10° ….. cot 85° is
(a) 0
(b) –1
(c) 1
(d) 2
Answer
C
Question. If sin 2θ + sin 2Φ = 1/2 and cos 2θ + cos 2Φ = 3/2 ,then cos2 (θ – Φ) =
(a) 3/8
(b) 5/8
(c) 3/4
(d) 5/4
Answer
B
Question. If tan θ = – 1/√3 , then general solution of the equation is
(a) 2nπ + π/6 , n ∈ I
(b) nπ + π/6 , n ∈ I
(c) 2nπ – π/6 , n ∈ I
(d) nπ – π/6 , n ∈ I
Answer
D
Question. cot x cot 2x – cot 2x cot 3x – cot 3x cot x is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
Question. A circular wire of radius 3 cm is cut and bent so as to lie along the circumference of a hoop whose radius is 48 cm. The angle in degrees which is subtended at the centre of hoop is
(a) 21.5°
(b) 23.5°
(c) 22.5°
(d) 24.5°
Answer
C
Question. π radian in degree measure is equal to
(a) 18°
(b) 180°
(c) 200°
(d) 360°
Answer
B
Question. sin 6θ + sin 4θ + sin 2θ = 0, then θ =
(a) nπ/4 or nπ ± π/3
(b) nπ/4 or nπ ± π/6
(c) nπ/4 or 2nπ ± π/6
(d) None of these
Answer
A
Question. Value of 2cosπ/13cos9π/13+cos3π/13+cos5π/13 is
(a) –1/2
(b) 0
(c) 1
(d) √3/2
Answer
B
Question. The value of tan(α + β), given that cot α = 1/2, α ∈ (π, 3π/2) and sec β = –5/3 , β ∈ (π/2, π) is
(a) 1/11
(b) 2/11
(c) 5/11
(d) 3/11
Answer
B
Question. 1/sin 10° – √3/cos 10° =
(a) 0
(b) 1
(c) 2
(d) 4
Answer
D
Question. If sin 3θ = sinθ , then the general value of θ is:
a. 2nπ(2n+1)π/3
b. nπ(2n+1)π/4
c. nπ(2n+1)π/3
d. None of these
Answer
B
Question. If tanθ + tan 2θ +√3 tanθ tan 2θ = √3 then:

Answer
C
Question. The angle subtended at the centre of radius 3 metres by the arc of length 1 metre is equal to:
a. 20º
b. 60º
c. 1/3 radian
d. 3 radian
Answer
C
Question. General value of θ satisfying the equation tan2θ + sec2θ = 1 is:
a. mπ , nπ + π/3
b. mπ , nπ ± π/3
c. mπ , nπ ± π/6
d. None of these
Answer
B
Question. The most general value of θ satisfying the equation tan θ = −1 and cosθ = 1/√2 is:
a. nπ + 7π/4
b. nπ + (−1)n 7π/4
c. 2nπ + 7π/4
d. None of these
Answer
C
Question. If tan
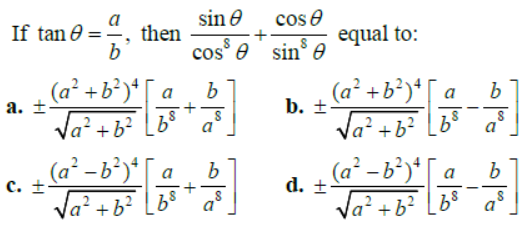
Answer
A
Question. If A + B + C = π , then cos2A + cos2B − cos2C equal to:
a. 1− 2 sin Asin B cosC
b. 1− 2 cos Acos B sin C
c. 1+ 2 sin Asin B cosC
d. 1+ 2 cos Acos B sin C
Answer
A
Question. If tan A + cot A = 4, then 4 4 tan A + cot A is equal to:
a. 110
b. 191
c. 80
d. 194
Answer
D
Question. If sin + cosx = 1/5 then tan 2x is:
a. 25/17
b. 7/25
c. 25/7
d. 24/7
Answer
D
Question. If sinx = 24/25 then the value of tan x is:
a. 24/25
b. 24/7
c. 25/24
d. None of these
Answer
B
Question. For
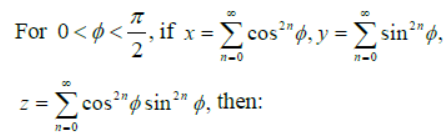
a. xyz = xz + y
b. xyz = xy + z
c. xyz = x + y + z
d. Both (b) and (c)
Answer
D
Question. sin 75º = :
a. 2–√3/2
b. √3+1/2√2
c. √3–1/2√2
d. √3–1/2√2
Answer
B
Question. The minute hand of a clock is 10 cm long. How far does the tip of the hand move in 20 minutes?
a. 10π/3
b. 20π/3
c. 30π/3
d. 40π/3
Answer
B
Question. If 4 sinθ = 3cosθ then Sec2θ/4[1–tan2θ] equals to:
a. 25/16
b. 25/28
c. 1/4
d. 1
Answer
B
Question.
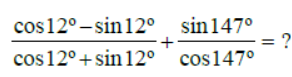
a. 2 tan 33º
b. 1
c. – 1
d. 0
Answer
D
Question. If 1 2 3 sinθ + sinθ + sinθ = 3, then cosθ1 + cosθ2 + cosθ3 = ?
a. 3
b. 2
c. 1
d. 0
Answer
D
Question. sin 47º + sin 61º − sin11º − sin 25º = ?
a. sin 36º
b. sin 7º
c. cos 36º
d. cos 7º
Answer
D
Question. The circular wire of radius 7 cm is cut and bend again into an arc of a circle of radius 12 cm. The angle subtended by an arc at the centre of the circle is:
a. 50º
b. 210º
c. 100º
d. 60º
Answer
B
Question. The degree measure corresponding to the given radian [2π/15]c
a. 21º
b. 22º
c. 23º
d. 24º
Answer
D
Question. sin163º cos 347º + sin 73º sin167º = ?
a. 0
b. 1/2
c. 1
d. None of these
Answer
B
Question. The value of cot 70º + 4 cos 70º is:
a. 1/√3
b. √3
c. 2√3
d. 1/2
Answer
B
Question. If sinα = −3/5 where π<α < 3π/2, then cos α/2 equal to:
a. 1/√10
b. –1/√10
c. 3/√10
d. –3/√10
Answer
D
Question.

a. tan(A− B)
b. tan(A+ B)
c. cot(A− B)
d. cot(A+ B)
Answer
B
Question. 2sin2 β + 4cos(α +β )sinα sinβ + cos2(α +β ) equal to: a. sin 2α b. cos 2β c. tan A / 2 d. sin 2β C
Answer
Question. cot 15º –1/cot 15º +1 = ?
a. 1/2
b. 3/2
c. 3√3/4
d. √3
Answer
B
Question. If sin2θ + sin 2Φ = 1/2 and cos2θ + cos2Φ =3/2 then 2 cos (θ −φ ) equal to:
a. 3/8
b. 5/8
c. 3/4
d. 5/4
Answer
B
Question. If x = ycos 2π/3 cos = zcos 4π/3 then xy + yz + zx = :
a. −1
b. 0
c. 1
d. 2
Answer
B
Question. If α + β +γ = 2π , then:
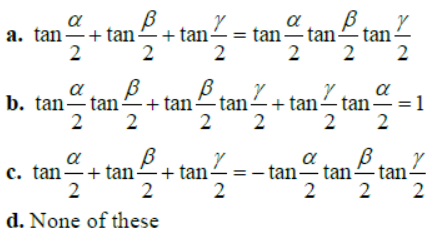
Answer
A
Question. If tan β = cosθ . tanα then tan2 θ/2 equal to:

Answer
A
Question. The general solution of tan 3x = 1 is :

Answer
A