VBQs Binomial Theorem Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Binomial Theorem Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Binomial Theorem VBQs Class 11 Mathematics
Question. r and n are positive integers r > 1, n > 2 and coefficient of (r+2)th term and 3rth term in the expansion of (1 + x)2n are equal, then n equals
(a) 3r
(b) 3r + 1
(c) 2r
(d) 2r + 1
Answer
C
Question. In every term, the sum of indices of a and b in the expansion of (a + b)n is
(a) n
(b) n + 1
(c) n + 2
(d) n – 1
Answer
A
Question. The term independent of x in the expansion of (6√x – 1/3√x )9 is
(a) – 9C3
(b) – 9C4
(c) – 9C5
(d) – 8C3
Answer
A
Question. The coefficient of the term independent of x in the expansion of
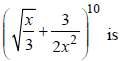
(a) 5/4
(b) 7/4
(c) 9/4
(d) None of these
Answer
A
Question. If in the binomial expansion of (1 + x)n where n is a natural number, the coefficients of the 5th, 6th and 7th terms are in A.P., then n is equal to:
(a) 7 or 13
(b) 7 or 14
(c) 7 or 15
(d) 7 or 17
Answer
B
Question. The coefficient of x–7 in the expansion of [ax – 1/bx2]–11 will be :
(a) 462a6/b5
(b) 462a5/b6
(c) –462a5/b6
(d) –462a6/b5
Answer
B
Question. One value of α for which the coefficients of the middle terms in the expansion of (1 + αx)4 and (1 – αx)6 are equal, is –3/10 . Other value of ‘α’ is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. If (1 + ax)n = 1 + 8x + 24 x2 + … then the values of a and n are
(a) n = 4, a = 2
(b) n = 5, a = 1
(c) n = 8, a = 3
(d) n = 8, a = 2
Answer
A
Question. The number of term in the expansion of [(x + 4y)3 (x – 4y)3]2 is
(a) 6
(b) 7
(c) 8
(d) 32
Answer
B
Question. If x is so small that x3 and higher powers of x may be neglected, then
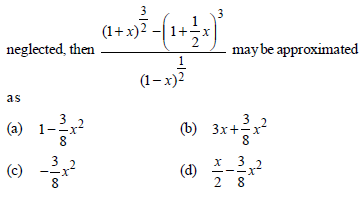
Answer
C
Question. In the expansion of (3√x/3 – √3/x)10 , x > 0, the constant term is
(a) –70
(b) 70
(c) 210
(d) –210
Answer
C
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 3 1 4 2
(b) 2 1 4 3
(c) 2 4 1 3
(d) 3 4 1 2
Answer
D
Question. The approximation of (0.99)5 using the first three terms of its expansion is
(a) 0.851
(b) 0.751
(c) 0.951
(d) None of these
Answer
C
Question. Notation form of (a + b)n is
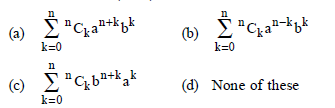
Answer
B
Question. If the fourth term in the expansion of (ax + 1/x)n is 5/2 , then the value of a × n is
(a) 2
(b) 6
(c) 3
(d) 4
Answer
C
Question. The coefficient of xn in expansion of (1+ x)(1– x)n is
(a) (–1)n–1n
(b) (–1)n (1– n)
(c) (–1)n–1(n –1)2
(d) (n –1)
Answer
B
Question. If the rth term in the expansion of (x/3 – 2/x2)10 contains x4, then the value of r is
(a) 2
(b) 3
(c) 4
(d) 5
Answer
B
Question. 1/√5+ 4x can be expanded by binomial theorem, if
(a) x < 1
(b) | x | < 1
(c) | x | < 5/4
(d) | x | < 4/5
Answer
C
Question. The term independent of x in the expansion of (1 – x/1 + x)2 is
(a) 4
(b) 3
(c) 1
(d) None of these
Answer
C
Question. Coefficient of x13 in the expansion of (1 – x)5 (1 + x + x2 + x3)4 is
(a) 4
(b) 6
(c) 32
(d) 5
Answer
A
Question. If A and B are coefficients of xn in the expansion of (1+ x)2n and (1+ x)2n –1 then :
(a) A = B
(b) 2A = B
(c) A = 2B
(d) AB = 2
Answer
C
Question. The coefficient of x–12 in the expansion of (x + y/x3)20
(a) 20C8
(b) 20C8 y8
(c) 20C12
(d) 20C12 y12
Answer
B
Question. What are the values of k if the term independent of x in the expansion of (√x + k/x2)10 is 405?
(a) ± 3
(b) ± 6
(c) ± 5
(d) ± 4
Answer
A
Question. In the expansion of (1 + x)18 , if the coefficients of (2r + 4)th and (r – 2)th terms are equal, then the value of r is :
(a) 12
(b) 10
(c) 8
(d) 6
Answer
D
Question. The expansion of 1/(4 – 3x)1/ 2 by binomial theorem will be valid, if
(a) x < 1
(b) | x | < 1
(c) –2/√3 <x<2/√3
(d) None of these
Answer
D
STATEMENT TYPE QUESTIONS
Question. Consider the following statements.
I. Coefficient of xr in the binomial expansion of (1 + x)n is nCr.
II. Coefficient of (r + 1)th term in the binomial expansionof (1 + x)n is nCr.
Choose the correct option.
(a) Only I is correct
(b) Only II is correct
(c) Both are correct.
(d) Both are incorrect.
Answer
C
Question. Consider the following statements.
I. General term in the expansion of (x2 – y)6 is ( – 1)r x12 – 2r · yr
II. 4th term in the expansion of (x – 2y)12 is –1760x9y3.
Choose the correct option.
(a) Only I is false
(b) Only II is false
(c) Both are false
(d) Both are true
Answer
A
Question. Consider the following statements.
I. The number of terms in the expansion of (x + a)n is n + 1.
II. The binomial expansion is briefly written as
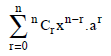
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
C
Question. Consider the following statements.
Binomial expansion of (x + a)n contains (n + 1) terms.
I. If n is even, then (n/2 + 1)th term is the middle term.
II. If n is odd, then (n + 1/2)th is the middle term.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
A
Question. The largest term in the expansion of (3 + 2x)50, where x=1/5 , is
I. 5th
II. 3rd
III. 7th
IV. 6th
Choose the correct option
(a) Only I
(b) Only II
(c) Both I and IV
(d) Both III and IV
Answer
D
Question. Consider the following statements.
I. General term of the expansion of (x + y)n is nCr xn – r yr.
II. The coefficients nCr occuring in the binomial theorem are known as binomial coefficients.
Choose the correct option.
(a) Only I is true
(b) Only II is true
(c) Both are true
(d) Both are false
Answer
C