Students should refer to Worksheets Class 12 Mathematics Matrices Chapter 3 provided below with important questions and answers. These important questions with solutions for Chapter 3 Matrices have been prepared by expert teachers for Class 12 Mathematics based on the expected pattern of questions in the class 12 exams. We have provided Worksheets for Class 12 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Matrices Worksheets Class 12 Mathematics
Question.
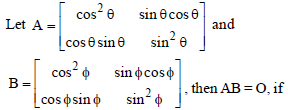
(a) θ = nΦ, n = 0, 1, 2, ……
(b) θ + Φ = n π , n = 0, 1, 2, …..
(c) θ = Φ + (2n + 1) π/2, n = 0, 1, 2, …
(d) θ = Φ + nπ/2, n = 0, 1, 2, …
Answer
C
Question.
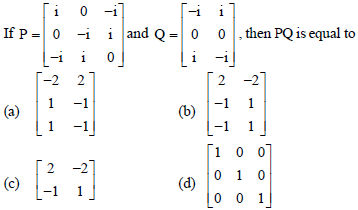
Answer
B
Question.
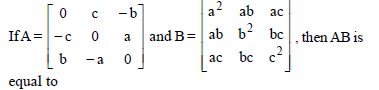
(a) B
(b) A
(c) O
(d) I
Answer
C
Question.
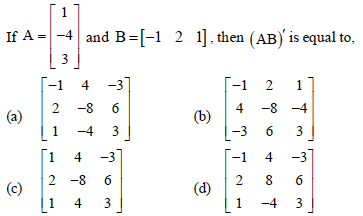
Answer
A
Question. Consider the matrix

(a) 2
(b) 3
(c) 4
(d) 5
Answer
B
Question. If A and B are 2 × 2 matrices, then which of the following is true?
(a) (A + B)2 = A2 + B2 + 2AB
(b) (A – B)2 = A2 + B2 – 2AB
(c) (A – B) (A + B) = A2 + AB – BA – B2
(d) (A + B) (A – B) = A2 – B2
Answer
C
Question.
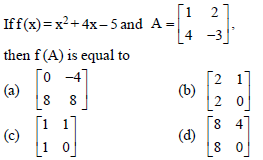
Answer
D
Question.
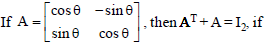
(a) θ = nπ, n ∈ Z
(b) θ =(2n + 1) , π/2 ,n ∈ Z
(c) θ = 2nπ + π/3, n ∈ Z
(d) None of these
Answer
C
Question.

[F(α)]−1 is equal to
(a) F(−α )
(b) F(α −1)
(c) F(2α )
(d) None of these
Answer
A
Question. If A and B are two matrices such that A + B and AB are both defined, then
(a) A and B are two matrices not necessarily of same order.
(b) A and B are square matrices of same order.
(c) Number of columns of A = Number of rows of B.
(d) None of these.
Answer
B
Question.
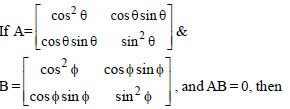
(a) (θ – Φ) is a multiple of π/2
(b) (θ – Φ) is an even multiple of π/2
(c) (θ – Φ) is a multiple of π/3
(d) (θ – Φ) is an odd multiple of π/2
Answer
D
Question. If A is a square matrix such that A2 = A, then (I + A)3 – 7A is equal to
(a) A
(b) I – A
(c) I
(d) 3 A
Answer
C
Question.

Answer
C
Question.
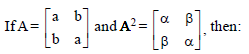
(a) α = a2 + b2, β = ab
(b) α = a2 + b2, β = 2ab
(c) α = a2 + b2, β = a2 – b2
(d) α = 2ab, β = a2 + b2
Answer
B
Question. The construction of 3 × 4 matrix A whose elements aij is

Answer
C
Question. If A and B are two square matrices such that B = – A–1 BA, then (A + B)2 =
(a) O
(b) A2 + B2
(c) A2 + 2 AB + B2
(d) A + B
Answer
B
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.
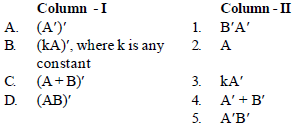
Codes
A B C D
(a) 2 4 3 5
(b) 1 4 3 2
(c) 3 1 4 2
(d) 2 3 4 1
Answer
D
Question.
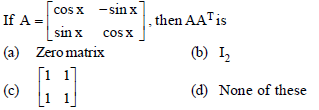
Answer
B
Question.
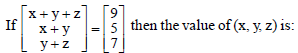
(a) (4, 3, 2)
(b) (3, 2, 4)
(c) (2, 3, 4)
(d) None of these
Answer
C
Question. If A is a square matrix of order m with elements aij, then
(a) A = [aij]n × n
(b) A = [aji]m × n
(c) A = [aij]m × m
(d) A = [aji]n × n
Answer
C
Question. If A is a square matrix such that (A – 2I) (A + I) = 0, then A–1 =
(a) A–I/2
(b) A+I/2
(c) 2 (A – I)
(d) 2A + I
Answer
A
Question.
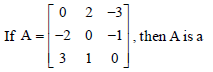
(a) symmetric matrix
(b) skew-symmetric matrix
(c) diagonal matrix
(d) none of these
Answer
B
Question. A square matrix B = [bij] m × m is said to be a diagonal matrix, if
(a) all its non-diagonal elements are non-zero i.e., bji ≠ 0; i ≠ j
(b) all its diagonal elements are zero, i.e., bji = 0, i = j
(c) all its non-diagonal elements are zero i.e, bji = 0 when i ≠ j
(d) None of the above
Answer
C
Question. If A2 – A + I = O, then the inverse of A is
(a) I – A
(b) A – I
(c) A
(d) A + I
Answer
A
Question. A square matrix A = [aij]n×n is called a diagonal matrix if aij = 0 for
(a) i = j
(b) i < j
(c) i > j
(d) i ≠ j
Answer
D
Question. Match the terms given in column-I with the terms given in column-II and choose the correct option from the codes given below.

Codes
A B C D
(a) 2 3 1 4
(b) 3 1 4 2
(c) 3 4 1 2
(d) 4 3 2 1
Answer
B
Question.
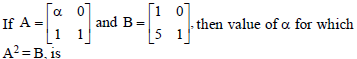
(a) 1
(b) –1
(c) 4
(d) no real values
Answer
D
Question.
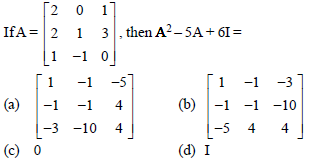
Answer
B
Question.
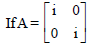
then A4n where n is a natural number, equals :
(a) I
(b) – A
(c) – I
(d) A
Answer
C
Question. A square matrix B = [bji]n × n is said to be a scalar matrix, if
(a) bji = 0 for i ≠ j and bji = k for i = j, for some constant k
(b) bji = 0 for i = j
(c) bji ≠ 0 for i = j and bji = 0 for i = j
(d) None of the above
Answer
A
Question. For a matrix A, AI = A and AAT = I is true for
(a) If A is a square matrix.
(b) If A is a non singular matrix.
(c) If A is symmetric matrix.
(d) If A is any matrix.
Answer
A
Question. If A and B are matrices of same order, then (AB’− BA’) is a
(a) skew symmetric matrix
(b) null matrix
(c) symmetric matrix
(d) unit matrix
Answer
A
Question.
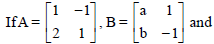
and (A + B)2 = A2 + B2 + 2AB, then values of a and b are
(a) a = 1, b = –2
(b) a = 1, b = 2
(c) a = –1, b = 2
(d) a = –1, b = –2
Answer
D
Question.
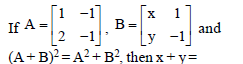
(a) 2
(b) 3
(c) 4
(d) 5
Answer
D
Question. Each diagonal element of a skew-symmetric matrix is
(a) zero
(b) positive
(c) non-real
(d) negative
Answer
A
Question. For what values of x and y are the following matrices equal
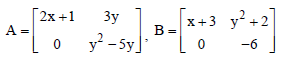
(a) 2, 3
(b) 3, 4
(c) 2, 2
(d) 3, 3
Answer
C
Question.
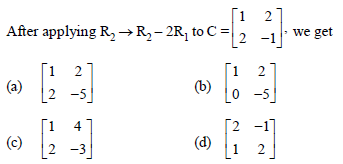
Answer
B
Question. If A is a 3 × 2 matrix, B is a 3 × 3 matrix and C is a 2 × 3 matrix, then the elements in A, B and C are respectively
(a) 6, 9, 8
(b) 6, 9, 6
(c) 9, 6, 6
(d) 6, 6, 9
Answer
B
Question.
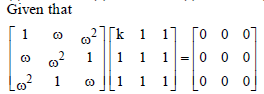
then k =
(a) 6
(b) 1
(c) 8
(d) 9
Answer
B
Question.
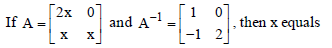
(a) 2
(b) −1/2
(c) 1
(d) 1/2
Answer
D
Question. If A = [aij]2×2, where aij = (i + 2j)2/2, then A is equal to
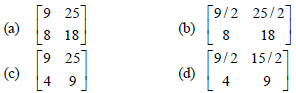
Answer
B
Question.
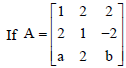
is a matrix satisfying AAT = 9I3, then the values of a and b respectively are
(a) 1, 2
(b) – 2, – 1
(c) – 1, 2
(d) – 2, 1
Answer
B
Question. If A is matrix of order m × n and B is a matrix such that AB’and B’A are both defined, then order of matrix B is
(a) m × m
(b) n × n
(c) n × m
(d) m × n
Answer
D
Question.
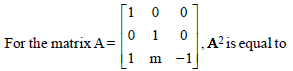
(a) 0
(b) A
(c) I
(d) None of these
Answer
C
Question.
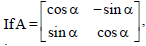
then A + A’ = I, then the value of α is
(a) π/6
(b) π/3
(c) π
(d) 3π/2
Answer
B

