Please refer to Class 12 Physics Sample Paper Term 1 Set F with solutions below. The following CBSE Sample Paper for Class 12 Physics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Physics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
CBSE Class 12 Physics Sample Paper for Term 1
SECTION – A
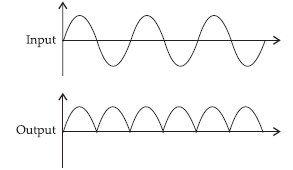
Question 1. In half-wave rectification, what is the output frequency if the input frequency is 50 Hz. What is the output frequency of a full-wave-rectifier for the same input frequency?
OR
What is hole in semiconductor?
Answer. In half wave rectification, only one ripple is obtained per cycle in the output.
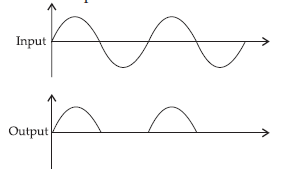
Output frequency of a half wave rectifier = input frequency = 50 Hz
In full wave rectification, two ripples are obtained per cycle in the output.
Output frequency = 2 × input frequency
= 2 × 50 = 100 Hz
OR
A vacancy is created when an electron leaves a covalent bond. This vacancy is known as hole.
Question 2. Why is the core of a transformer laminated ?
Answer.The core of a transformer is laminated to reduce the energy losses due to eddy currents, so that its efficiency may remain nearly 100%.
Question 3. Name the series of hydrogen spectrum lying in infra-red region.
Answer.Paschen series lies in infra-red region.
Question 4. Write the expression for the speed of light in a material medium of relative permittivity er and relative magnetic permeability mr.
Answer.The speed of electromagnetic wave in a medium,
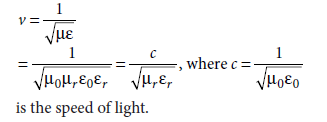
Question 5. At a given place on the earth’s surface, the horizontal component of earth’s magnetic field is 3 × 10–5 T and resultant magnetic field is 6 × 10–5 T. Calculate the angle of dip at this place.
OR
The horizontal and vertical components of earth’s magnetic field at a place are 0.3 G and 0.52 G. Find the earth’s resultant magnetic field and the angle of dip.
Answer.

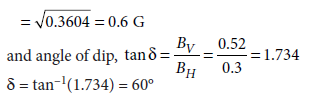
Question 6. Write the conditions on path difference under which (i) constructive (ii) destructive interference occur in Young’s double slit experiment.
Answer. For constructive interference,
Path difference, Dx = nl (where n = 0, 1, 2, …)
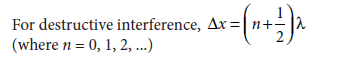
Question 7. Explain the term “sharpness of resonance” in ac circuit.
Answer. Sharpness of resonance : It is defined as the ratio of the voltage developed across the inductance (L) or capacitance (C) at resonance to the voltage developed across the resistance (R).
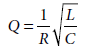
It may also be defined as the ratio of resonant angular frequency to the bandwidth of the circuit.
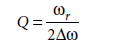
Question 8. The conductivity of a semiconductor increases with increase in temperature. Give reason.
OR
In a circuit as shown in the figure, the diode forward voltage drop is 0.3 V, the voltage difference between A and B?
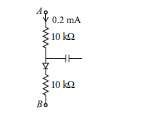
Answer.In a semiconductor, with rise in temperature number density of current carries increases, relaxation time decreases but effect of decrease in relaxation time is much less than the increase in number density.
OR
Let V be the potential difference between A and B, then
V – 0.3 = (10 + 10) × 103 × (0.2 × 10–3) = 4
or V = 4 + 0.3 = 4.3 V
Question 9. A resistance R is connected across a cell of emf e and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell as V. Write the expression for r in terms of e, V and R.
Answer.
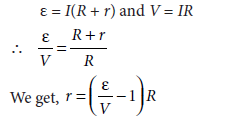
Question 10. Name the electromagnetic radiation used for water purification, and eye surgery.
OR
What do you understand by the statement, “Electromagnetic waves transport momentum”?
For question numbers 11, 12, 13 and 14, two statements are given-one labelled Assertion (A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
Answer.Ultraviolet rays.
OR
Electromagnetic waves transport momentum means that electromagnetic waves carry momentum from one place to another as they travel through medium or space.
Question 11. Assertion (A) : In the absence of an externally applied electric field, the displacement per unit volume of a polar dielectric material is always zero.
Reason (R) : In polar dielectrics, each molecule has a permanent dipole moment but these are randomly oriented in the absence of an externally applied electric field.
Answer
A
Question 12. Assertion (A) : Only a change in magnetic flux will maintain an induced current in the coil.
Reason (R) : The presence of large magnetic flux through a coil maintains a current in the coil if the circuit is continuous.
Answer
C
Question 13. Assertion (A) : Static crashes are heard on radio, when lightning flash occurs in the sky.
Reason (R) : Electromagnetic waves having frequency of radio wave range interfere with radio waves.
Answer
A
Question 14. Assertion (A) : The energy of charged particle moving in a uniform magnetic field does not change.
Reason (R) : Work done by magnetic field on the charge is zero.
Answer
D
SECTION – B
Question 15. An electric potential is the amount of work needed to move a unit of electric charge from a reference point to a specific point in an electric field without producing an acceleration. Typically, the reference point is the Earth or a point at infinity, although any point can be used. This value can be calculated in either a static (time‐invariant) or a dynamic (varying with time) electric field at a specific time in units of joules per coulomb (J C− 1), or volts (V). The electric potential at infinity is assumed to be zero.
(i) In bringing an electron towards another electron, the electrostatic potential energy of the system
(a) increases
(b) decreases
(c) remains uncharged
(d) becomes zero.
Answer
A
(ii) Some charge is being given to conductor. Then, its potential
(a) is maximum at surface.
(b) is maximum at centre
(c) remains the same throughout the conductor
(d) is maximum somewhere between surface and centre.
Answer
C
(iii) A point charge +q is placed at the origin O. Work done in taking another point charge –Q from the point A (0, a) to another point B (a, 0) along the straight path AB is

Answer
D
(iv) Two charge q1 and q2 are placed 30 cm apart as show in the figure. A third charge q3 is moved along the circular path of radius 40 cm from C to D. The change in the potential energy of the system is q3/4πε0 k,where k is
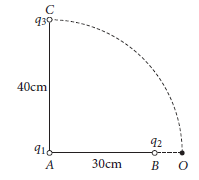
(a) 8 q1
(b) 6 q1
(c) 8 q2
(d) 6 q2
Answer
C
(v) The electric potential at a point (x, y) in (x-y) plane is given by V = −xy. The field intensity at a distance r from origin varies as
(a) r2
(b) r
(c) 1/r
(d) 1/r2
Answer
B
Question 16. According to Einstein, when a photon of light of frequency u or wavelength l is incident on a photosensitive metal surface of work function Φ0, where Φ0 < hu (here, h is Planck’s constant), then the emission of photoelectrons takes place. The maximum kinetic energy of the emitted photoelectrons is given by Kmax = hu – f0. If the frequency of the incident light is u0 (called threshold frequency), the photoelectrons are emitted from metal without any kinetic energy. So hu0 = Φ0.
(i) The photoelectric emission could be explained by the ________.
(a) wave nature of light
(b) particle nature of light
(c) dual nature of light
(d) quantum nature
Answer
B
(ii) A metal of work function 3.3 eV is illuminated by light of wavelength 300 nm. The maximum kinetic energy of photoelectron emitted is (taking h = 6.6 × 10–34 J s)
(a) 0.413 eV
(b) 0.825 eV
(c) 1.65 eV
(d) 1.32 eV
Answer
B
(iii) The variation to maximum kinetic energy (Kmax) of the emitted photoelectrons with frequency (u) of the incident radiations can be represented by

Answer
A
(iv) The variation of photoelectric current (i) with the intensity of the incident radiation (I) can be represented by
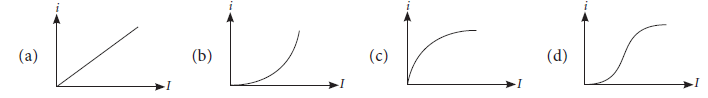
Answer
A
(v) Photons of energy 8 eV are incident on a potassium surface whose work function is 2.1 eV. The corresponding stopping potential required is
(a) 7.3 V
(b) 8.1 V
(c) 5.9 V
(d) 2.7 V
Answer
C
SECTION – C
Question 17. A beam of light travelling along x-axis is described by the magnetic field,
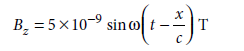
Calculate the maximum magnetic forces on an alpha particle moving along y-axis with a speed of 3 × 107 m s–1. (Charge on electron = 1.6 × 10–19 C)
Answer.B
Here, B0 = 5 × 10–9 T ;
charge on alpha particle, q = + 2e = 2 × 1.6 × 10–19
= 3.2 × 10–19 C,
v = 3 × 107 m s–1
Force on alpha particle due to magnetic field = qvB0
= (3.2 × 10–19) × (3 × 107) × (5 × 10–9)
= 4.80 × 10–20 N.
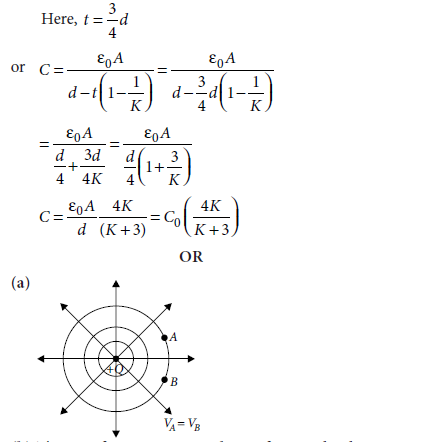
Question 18. A slab of material of dielectric constant K has the same area as the plates of a parallel plate capacitor, but has a thickness 3/4 d , where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates?
OR
(a) Draw equipotential surfaces due to point Q > 0.
(b) Are these surfaces equidistant from each other? If no, explain why?
Answer.

Question 19. A lamp is connected in series with a capacitor. Predict your observation when this combination is connected in turn across (i) ac source and (ii) a dc battery. What change would you notice in each case if the capacitance of the capacitor is increased?
Answer.
(i) As ω = 0 for dc, capacitive reactance, Xc will be infinite and hence no current will flow in the circuit. So the lamp will not glow even if we change the capacitance.
(ii) On the other hand as XC will be finite in a.c connections. Current will flow through the lamp , so the lamp will glow. When we reduce C, XC increases and hence lamp will glow less bright.
Question 20. Define the terms (i) cut-off voltage and (ii) threshold frequency in relation to the phenomenon of photoelectric effect.
OR
In the wave picture of light, intensity of light is determined by the square of the amplitude of the wave. What determines the intensity in the photon picture of light?
Answer.
(i) Cut-off voltage : For a particular frequency (u > u0) of incident radiation, the minimum negative potential V0 applied to the plate or anode, (A) for
which the photoelectric current just becomes zero is called cut-off voltage.
(ii) Threshold frequency : It is defined as the minimum frequency of incident radiation below which the photoelectric emission stops altogether.
OR
For a given frequency, intensity of light in the photon picture is determined by
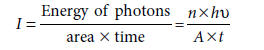
Where n is the number of photons incident normally on crossing area A in time t.
Question 21. What is the shape of the wavefront in each of the following cases:
(a) Light diverging from a point source.
(b) Light emerging out of a convex lens when a point source is placed at its focus.
(c) The portion of the wavefront of light from a distant star intercepted by the Earth.
Answer. (a) Spherical wavefront : All particles vibrating in same phase will lie on a sphere.
(b) Plane wavefront : Light will be a parallel beam after passing through the convex lens.
(c) Plane wavefront : Light rays from a distant star are nearly parallel as a small portion of a huge spherical wavefront is nearly plane.
Question 22. (i) Define the term ‘electric flux’. Write its SI unit.
(ii) What is the flux due to electric field E = 3 ×103 i N/C through a square of side 10 cm, when it is held normal to E ?
Answer. (i) Electric flux : Total number of electric field lines crossing a surface normally is called electric flux.
SI unit of electric flux is N m2 C–1.
(ii) The area of a surface can be represented as a vector along normal to the surface.
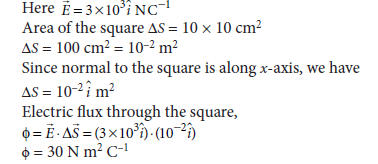
Question 23. The forbidden energy gap in semiconductors, insulators and metals are Es, Ei, and Em respectively. Arrange these in descending order. The band gap in silicon is 1.12 eV. What is the maximum wavelength of light that can be emitted by it?
OR
In the following diagram, which bulb out of B1 and B2 will glow and why?
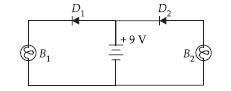
Answer.
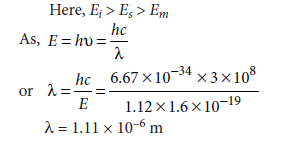
OR
Bulb B1 will glow, as diode D1 is forward biased. Bulb B2 will not glow as diode D2 is reverse biased.
Question 24. An equiconvex lens of focal length ‘f’ is cut into two identical plane convex lenses. How will the power of each part be related to the focal length of the original lens?
Answer. The focal length of original equiconvex lens is f.
Let the focal length of each part after cutting be F.
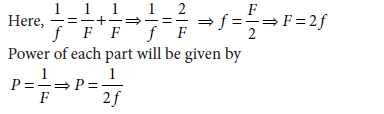
Question 25. Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20 cm. The distance of light source from the glass surface is 100 cm. At what position is the image formed ?
Answer.
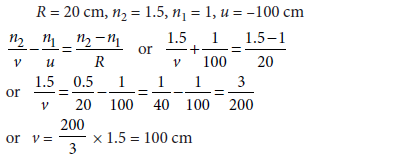
So, a real image is formed on the other side, 100 cm away from the surface.
SECTION – D
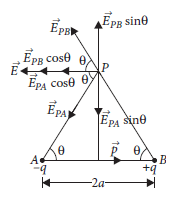
Question 26. Derive an expression for the electric field due to dipole of dipole moment p at a point on its perpendicular bisector.
Answer. Electric field on the equatorial line of an electric dipole : Electric field at any point on the perpendicular bisector of an electric dipole at distance r from its centre is
Enet = Ex = EPA cosθ + EPB cos θ (Vertical component cancel each other)

Question 27. A current is induced in coil C1 due to the motion of current carrying coil C2. (i) Write any two ways by which a large deflection can be obtained in the galvanometer G. (ii) Suggest an alternative device to demonstrate the induced current in place of a galvanometer.

OR
Two inductors of self-inductances L1 and L2 are connected in parallel. The inductors are so far apart that their mutual inductance is negligible. Derive the equivalent inductance of the combination.
Answer.
(i) To obtain large deflection in galvanometer we can take following steps :
(1) Connect the coil C2 to a powerful battery for large current.
(2) Switch on and off the key at a rapid rate.
(3) Develop a relative shift/motion between the two coils.
(4) Use a ferromagnetic material like iron inside the coil C2 to increase the magnetic flux.
(ii) Galvanometer is replaced by a torch bulb. Now a relative motion between two coils or switch on and off of the key glows the bulb and shows presence of induced current.
OR
Inductances in parallel : For the parallel combination, the total current I divides up through the two coils as
I = I1 + I2.

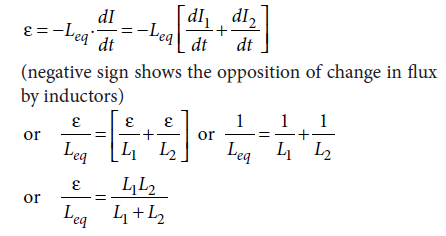
Question 28. Mention the important considerations required while fabricating a p-n junction diode to be used as a Light Emitting Diode (LED).
Answer. (i) There is very little resistance to limit the current in LED. Therefore, a resistor must be used in series with the LED to avoid any damage to it.
(ii) The reverse breakdown voltages of LEDs are very low, typically around 5 V. So care should be taken while fabricating a pn-junction diode so that the p side should only attached to the positive of battery and vice versa as LED easily get damaged by a small reverse voltage.
(iii) The semiconductor used for fabrication of visible LEDs must at least have a band gap of 1.8 eV (spectral range of visible light is from about 0.4 mm to 0.7 mm, i.e., from about 3 eV to 1.8 eV).
Question 29. Two monochromatic waves emanating from two coherent sources have the displacements represented by y1 = a cos wt and y2 = a cos (wt + f) where f is the phase difference between the two displacements.
Show that the resultant intensity at a point due to their superposition is given by I = 4 I0 cos2 Φ/2, where I0 = a2.
OR
A parallel beam of monochromatic light falls normally on a narrow slit of width ‘a’ to produce a diffraction pattern on the screen placed parallel to the plane of the slit.
Use Huygens’ principle to explain the necessary conditions of minima and maxima. Also draw the intensity pattern obtained on the screen.
Answer. y1 = a cos wt, y2 = a cos (wt +Φ)
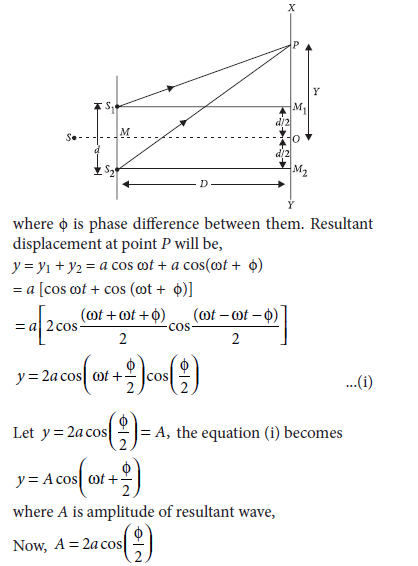
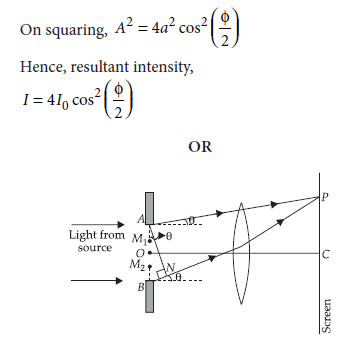
Consider a parallel beam of monochromatic light is incident normally on a single slit AB of width a as shown in the figure. According to Huygens principle every point of slit acts as a source of secondary wavelets spreading in all directions. The mid point of the slit is O.
A straight line through O perpendicular to the slit plane meets the screen at C. At the central point C on the screen, the angle q is zero. All path differences are zero and hence all the parts of the slit contribute in phase.
This gives maximum intensity at C. Consider a point P on the screen.
The observation point is now taken at P.

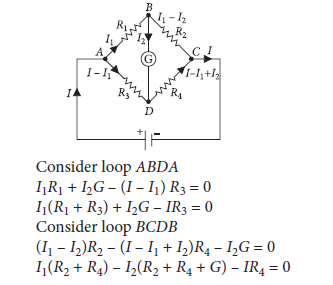
Question 30. Use Kirchhoff’s rules to obtain conditions for the balance condition in a Wheatstone bridge.
Answer.
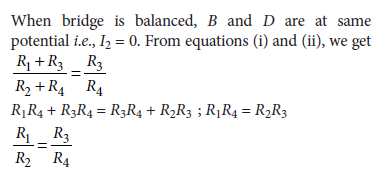
SECTION – E
Question 31. (a) Draw a ray diagram to show the working of a compound microscope. Deduce an expression for the total magnification when the final image is formed at the near point.
(b) In a compound microscope, an object is placed at a distance of 1.5 cm from the objective of focal length 1.25 cm. If the eye piece has a focal length of 5 cm and the final image is formed at the near point, estimate the magnifying power of the microscope.
OR
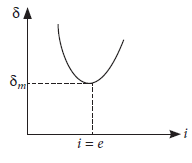
(a) Draw a graph showing variation of angle of deviation with angle of incidence when a ray of monochromatic light passing through a glass prism.
(b) Deduce the expression for the refractive index of glass in terms of angle of prism and angle of minimum deviation.
Answer.
(a) Formation of image by a compound microscope :
A schematic diagram of a compound microscope is shown in figure :

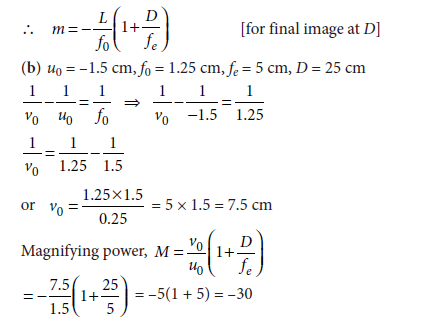
(a) If graph is plotted between angle of incidence i and angle of deviation d, it is found that the angle of deviation d first decreases with increase in angle of incidence i and then becomes minimum ‘dm’ when i = e and then increases with increase in angle of incidence i.
(b) Figure shows the path of a ray of light suffering refraction through a prism of refracting angle ‘A’. At minimum deviation, the inside beam travels parallel to base of the prism.
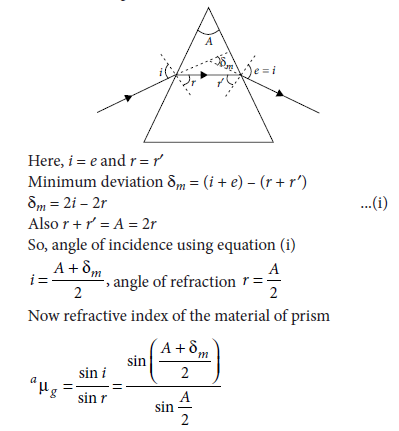
where A is the refracting angle of the prism and A = 60° for an equiangular prism.
Question 32. Using Ampere’s circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
OR
With the help of a circuit, show how a galvanometer can be converted into an ammeter of a given range.Write the necessary mathematical formula.
Answer. Magnetic field due to a toroidal
solenoid : A long solenoid shaped in the form of closed ring is called a toroidal solenoid (or endless solenoid). Let n be the number of turns per unit length of toroid and I the current flowing through it.
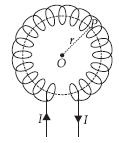
The current causes the magnetic field inside the turns of the toroid. The magnetic lines of force inside the toroid are in the form of concentric circles. By symmetry the magnetic field has the same magnitude at each point of circle and is along the tangent at every 0point on the circle.
For points inside the core of toroid
Consider a circle of radius r in the region enclosed by turns of toroid. Now we apply Ampere’s circuital law to this circular path, i.e.,

OR
An ammeter is a low resistance galvanometer and is connected in series in a circuit to read current directly in ampere.
The resistance of an ammeter is to be made as low as possible so that it may read current without any appreciable error. Therefore to convert a galvanometer into ammeter a shunt resistance (i.e. small resistance in parallel) is connected across the coil of galvanometer. Let G be the resistance of galvanometer and Ig the current required for full scale deflection. Suppose this galvanometer is to be converted into ammeter of range I ampere and the value of shunt required is S. If IS is current in shunt, then from figure.

If k is figure of merit of the galvanometer and n is the number of scale divisions, then Ig = nk. Out of the total main current I amperes, only a small permissible value Ig flows through the galvanometer and the rest IS = (I – Ig) passes through the shunt.
Question 33. How is the size of a nucleus experimentally determined? Write the relation between the radius and mass number of the nucleus. Show that the density of nucleus is independent of its mass number.
OR
(a) What is meant by size of nucleus? Are all nuclei of the same size?
(b) A nucleus of mass number 225 splits into two fresh nuclei having mass numbers in the ratio 3 : 2. If the nuclear radius is given by R = 1.1 × 10–15 A1/3 m, find the radii of the new nuclei formed.
Answer. Nucleus was first discovered in 1911 by Lord Rutherford and his associates by experiments on scattering of a-particle by atoms. He found that the scattering result could be explained, if atoms consists of a small, central, massive and positive core surrounded by orbiting electron. The experiment results indicated that the size of the nucleus is of the order of 10–14 metres and it thus 10,000 times smaller than the size of atom.
Relation between the radius and mass number of the
nucleus R = R0 A1/3
If m is the average mass of a nucleon and R is the nuclear radius, then mass of nucleus = mA, where A is the mass number of the element.
Volume of the nucleus, V = 4/3 π R3
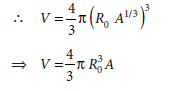
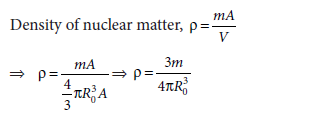
This shows that the nuclear density is independent of A.
OR
(a) The extremely small central core of the atom, in which whole of the positive charge and practically the entire mass is confined, is called nucleus.
All nuclei are not of the same size. The size (radius) of the nucleus is directly proportional to A1/3, where A is its mass number.
(b) Here, A = 225; R = 1.1 × 10–15 A1/3
Let A1 and A2 be the respective mass numbers of the two new nuclei formed.


