MCQ Chapter 12 Areas related to Circles Class 10 Mathematics

Please refer to Areas related to Circles MCQ Questions Class 10 Mathematics below. These MCQ questions for Class 10 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Areas related to Circles will help you to prepare for the exams and get more marks.

Areas related to Circles MCQ Questions Class 10 Mathematics

Please see solved MCQ Questions for Areas related to Circles in Class 10 Mathematics. All questions and answers have been prepared by expert faculty of standard 10 based on the latest examination guidelines.

MCQ Questions Class 10 Mathematics Areas related to Circles

Question. If the area of circle is numerically equal to twice its circumference, then the diameter of the circle is
(a) 4 units
(b) 6 units
(c) 8 units
(d) 12 units

Question. The perimeter (in cm) of a square circumscribing a circle of radius a cm is
(a) 2a
(b) 4a
(c) 6a
(d) 8a

Question. The cost of fencing a circular field at the rate of ₹ 24 per metre is ₹ 5280. The radius of the field is
(a) 15 m
(b) 35 m
(c) 25 m
(d) 30 m

Question. What is the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm?
(a) 20 cm
(b) 30 cm
(c) 50 cm
(d) 80 cm

Question. What is the area of the circle that can be inscribed in a square of side 6 cm?
(a) 9 π cm²
(b) 11 π cm²
(c) 16 π cm²
(d) 15 π cm²

Question. The area of a quadrant of a circle whose circumference is 25 cm is
(a) 24 cm²
(b) 28 cm²
(c) 32.5 cm²
(d) 38.5 cm²

Question. If area of quadrant of a circle is 38.5 cm², then its diameter is [Use π = 22/7]
(a) 10 cm
(b) 14 cm
(c) 21 cm
(d) None of these

Question. The areas of two circles are in the ratio 9 : 4, then what is the ratio of their circumferences?
(a) 1 : 2
(b) 2 : 1
(c) 3 : 2
(d) 2 : 3

Question. If the perimeter of a circle is equal to that of a square, then the ratio of their areas is
(a) 22 : 7
(b) 14 : 11
(c) 7 : 22
(d) 11 : 14

Question. The radii of two circles are 8 cm and 6 cm respectively. The radius of the circle having area equal to the sum of the areas of the two circles is
(a) 5 cm
(b) 10 cm
(c) 12 cm
(d) 15 cm

Question. An athlete runs on a circular track of radius 49 m and covers a distance of 3080 m along its boundary. How many rounds has he taken to cover this distance ? [Take π = 22 / 7]
(a) 5
(b) 8
(c) 10
(d) 15

Question. It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park is
(a) 10 m
(b) 12 m
(c) 15 m
(d) 18 m

Question. The area of the largest triangle that can be inscribed in a semi-circle of radius r units will be
(a) r sq. units
(b) r /2 sq. units
(c) r² sq. units
(d) 2r sq. units

Question. The cost of fencing a circular field at the rate of ₹ 24 per metre is ₹ 5280. The field is to be ploughed at the rate of ₹ 0.50 per m². The cost of ploughing the field is  [Take π = 22/ 7]
(a) ₹ 1925
(b) ₹ 1650
(c) ₹ 2010
(d) ₹ 2525

Question. The area of circle whose circumference is 22 cm is
(a) 32/ 2 cm²
(b) 45/ 2 cm²
(c) 55/ 2 cm²
(d) 77/2 cm²

Question. A road which is 7 m wide surrounds a circular park whose circumference is 88 m. The area of the road is
(a) 220 m²
(b) 340 m²
(c) 550 m²
(d) 770 m²

Question. In the given figure, a square of diagonal 8 cm is inscribed in a circle. The area of the shaded region is

(a) 12, 1/ 2 cm
(b) 18, 2/ 7 cm²
(c) 24, 3/ 4 cm²
(d) 11, 2/ 9 cm²

Question. The diameter of a circle whose circumference is equal to the sum of the circumference of the two circles of diameters 36 cm and 20 cm is
(a) 22 cm
(b) 32 cm
(c) 56 cm
(d) 84 cm

Question. The outer diameter and the inner diameter of a circular path are 728m and 700 m respectively. Find the area of the 22 circular path. (Use π = 22/7).   
(a) 45260 m²
(b) 25012 m²
(c) 31416 m²
(d) 19541 m²

Question. How many plants will be there in a circular bed whose outer edge measures 30 cm allowing 4 cm² for each plant?   
(a) 18
(b) 750
(d) 24
(d) 120

Question. Each wheel of a car makes 5 revolutions per second. If the diameter of a wheel is 84 cm, find the speed of the car in km/h.     
(a) 48 km / h
(b) 32 km / h
(c) 41 km / h
(d) 25 km / h

Question. The figure given shows a rectangle with a semicircle and 2 identical quadrants inside it. 

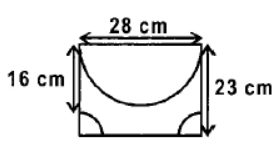
What is the shaded area of the figure? (Use π = 22/7).
(a) 363 cm²
(b) 259 cm²
(c) 305 cm²
(d) 216 cm²

Question. Mrs. Vidya bought a piece of cloth as shown in the figure. The portion of the cloth that is not coloured consists of 6 identical semicircles. 

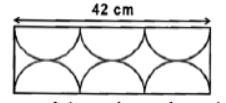
Find the area of the coloured portion.
(a) 144 cm²
(b) 126 cm²
(c) 195 cm²
(d) 243 cm²

Question. A regular hexagon is inscribed in a circle of radius 14 cm. Find the area of the circle falling outside the hexagon.   
(a) 106.79 cm²
(b) 241.8 cm²
(c) 79.27 cm²
(d) 173.9 cm²

Question. A sector of120° cut out from a circle has an area of 9 , 3/7 . What is the radius of the circle?     
(a) 3cm
(b) 2.5 cm
(c) 3.5 cm
(d) 3.6 cm

Question. In the given figure, O is the centre of the circle whose diameter is 14 cm.   
Find the perimeter of the figure. (Use π = 22/7) .
(a) 134cm
(b) 124cm
(c) 112cm
(d) 160cm

Question. David cut out the given figure during one of his art classes. The figure is made up of rectangles and quadrants.   

If David wanted to colour the figure red. Find the total area that he needs to colour. (Use π = 3.14 )
(a) 383.68 cm²
(b) 197.59 cm²
(c) 173.45 cm²
(d) 242.52 cm²

Question. Find the area of the sector of a circle, whose radius is 6 m when the angle at the centre is 42° .   
(a) 13. 2m²
(b) 14. 2m²
(c) 13. 4m²
(d) 14. 4m²

Question. A square shaped bus shelter is supported on four circular poles-The circumference of each pole is ‘x’ m and the length of each side of the shelter is ‘y’ m. Find the area of the unsupported part of the shelter.   
(a) (x² – y²/p)m²
(b) (y² + x²/p)m²
(c) (x² – y²/p)m²
(d) (y² – x²/p)m²

Question. Four equal circles are described about the four corners of a square so that each of them touches two of the others. If each side of the square measures 14 cm, find the area of the remaining portion of the square apart from four circles in cm² .     
(a) 20
(b) 24
(c) 42
(d) 40

Question. If the circumference of a circle is increased by 50%, by what percent will its area be increased?   
(a) 75%
(b) 100%
(c) 125%
(d) 150%

Question. Kill In the given figure, ABC is a right-angled triangle in which ∠ABC = 90° , AB = 6 cm and BC = 8 cm. 0 is the centre of the in circle.   

Find the area of shaded region. (Use π = 22/7).     
(a) 12.56 cm²
(b) 11.42 cm²
(c) 13.65 cm²
(d) 10.57 cm²

Question. What is The area of a sector of a circle of radius 16 cm cut off by an arc which is 18.5 cm long?   
(a) 168 cm²
(b) 148 cm²
(c) 154 cm²
(d) 176 cm²

Question. The area of the square that can be inscribed in a circle of radius 8 cm is
(a) 256 cm²
(b) 128 cm²
(c) 64 √2 cm²
(d) 64 cm²

Question. The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is
(a) 31 cm
(b) 25 cm
(c) 62 cm
(d) 50 cm

Question. In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Choose the correct choice as:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
1. Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius.
2. Assertion (A): If the outer and inner diameter of a circular path is 10 m and 6 m respectively, then area of the path is 16 π m².
Reason (R): If R and r be the radius of outer and inner circular path respectively, then area of circular path = π (R² – r²).

Question. The area of the sector in the following figure showing a chord AB of a circle of radius 18 cm subtending an angle of 60° at the centre O is [Take π = 3.14]

(a) 151.31 cm²
(b) 169.56 cm²
(c) 173.33 cm²
(d) None of these

Question. A horse is tied to a pole with 28 m long rope. The perimeter of the field where the horse can graze is (Take π = 22/7)
(a) 60 cm
(b) 85 cm
(c) 124 cm
(d) 176 cm

Question. A car has two wipers which do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle 120°. The total area cleaned at each sweep of the blades is [Take π = 7/ 22 ]
(a) 360 cm²
(b) 448 cm²
(c) 556 cm²
(d) 924 cm

Question. In the given figure, APB and CQD are semicircles of diameter 7 cm each, while ARC and BSD are semicircles of diameter 14 cm each. The perimeter of the shaded region is [Take π = 7/ 22 ]

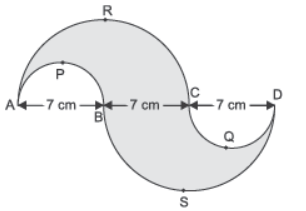
(a) 22 cm
(b) 33 cm
(c) 44 cm
(d) 66 cm

Question. A piece of wire 22 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. The radius of the circle is [Take π = 7/22 ]
(a) 7 cm
(b) 14 cm
(c) 21 cm
(d) 28 cm

Question. The area of the shaded region in the given figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle is [Take π = 3.14] 9

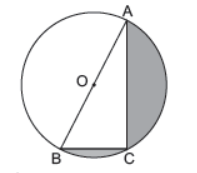
(a) 128.56 cm²
(b) 145.33 cm²
(c) 248.16 cm²
(d) None of these

Question. In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, the area of the shaded region is [Use π = 3.14]

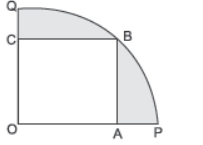
(a) 126 cm²
(b) 200 cm²
(c) 228 cm²
(d) None of these

Question. In the given figure, the shape of the top of a table is that of a sector of a circle with centre O and ∠AOB = 90°. If AO = OB = 42 cm, then the perimeter of the top of the table is [Take π = 7/ 22 ]

(a) 282 cm
(b) 266 cm
(c) 320 cm
(d) 480 cm

Question. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. The length of the arc is
(a) 11 cm
(b) 22 cm
(c) 27 cm
(d) 44 cm

Question. An arc of length 15.7 cm subtends a right angle at the centre of the circle. Then the radius of the circle is
(a) 20 cm
(b) 10 cm
(c) 15 cm
(d) 12 cm

Question. In the given figure, the boundary of shaded region consists of four semicircular arcs, two smallest being equal. If diameter of the largest is 14 cm and that of the smallest is 3.5 cm, the area of the shaded region is [Take π = 7/ 22 ]

(a) 72.225 cm²
(b) 86.625 cm²
(c) 92.330 cm²
(d) None of these

Question. The angle described by a minute hand in 5 minutes is
(a) 30°
(b) 60°
(c) 90°
(d) None of these

Question. The short and long hands of a clock are 4 cm and 6 cm long respectively. The sum of distances travelled by their tips in 2 days is
(a) 1148 cm
(b) 1426.35 cm
(c) 1910.85 cm
(d) None of these

Question. The area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm is
(a) 3.25 cm²
(b) 8.75 cm²
(c) 4.60 cm²
(d) 5.50 cm²

Question. The area of the largest circle that can be drawn inside the given rectangle of length ‘a’ cm and breadth ‘b’ cm (a > b) is
(a) 1/ 2 πb² cm²
(b) 1/ 3 πb² cm²
(c) 1/ 4 πb² cm²
(d) π b² cm²

Question. All the vertices of a rhombus lie on a circle. The area of the rhombus, if the area of the circle is 1256 cm2 is [Use π = 3.14]
(a) 300 cm²
(b) 600 cm²
(c) 800 cm²
(d) 900 cm²

Question. The difference of the areas of two segments of a circle formed by a chord of radius 5 cm subtending an angle of 90° at the centre is
(a) (25π/4 − 25/2) cm²
(b) (15π/ 4 − 7/ 2) cm²
(c) (7π/ 4 − 3/ 2) cm²
(d) None of these

Question. The area of the major segment APB in figure of a circle of radius 35 cm and ∠AOB = 90° is [Take π = 7/ 22 ]

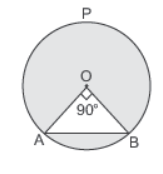
(a) 1200 cm²
(b) 2400 cm²
(c) 3500 cm²
(d) None of these

Question. In a circle of diameter 42 cm,if an arc subtends an angle of 60° at the centre where π = 22/ 7 , then what will be the length of arc ?
(a) 11 cm
(b) 20 cm
(c) 22 cm
(d) 28 cm

Question. In the given figure, PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. The perimeter of the shaded region is [Use π = 3.14]

(a) 22.5 cm
(b) 31.4 cm
(c) 36.6 cm
(d) None of these

Question. The given figure is a sector of circle of radius 10.5 cm. The perimeter of the sector is [Take π = 7/ 22 ]

(a) 32 cm
(b) 44 cm
(c) 54 cm
(d) None of these

Question. There are three semi-circles A, B and C having diameter 3 cm each and another semicircle E having a circle D with diameter 4.5 cm as shown in the figure. The area of the shaded region is

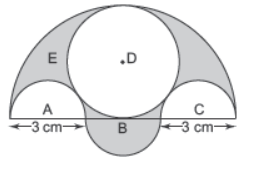
(a) 15 /16 π cm²
(b) 18 /19 π cm²
(c) 37 /54 π cm²
(d) 63 /16 π cm²

Question. The area of the shaded region given in the figure is

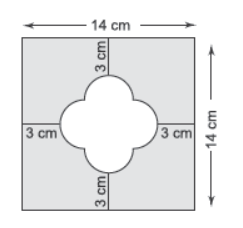
(a) (180 – 2π) cm²
(b) (90 – 8π) cm²
(c) (180 – 8π) cm²
(d) (90 – 2π) cm²

Question. The area of the shaded region in the given figure, if PR = 12 cm, PQ = 5 cm and O is the centre of the circle is [Take π = 7/ 22 ]

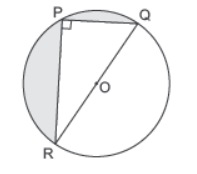
(a) 36.39 cm²
(b) 48.24 cm²
(c) 28.76 cm²
(d) 62.62 cm²

Question. If the perimeter and area of a circle are numerically equal; its radius will be   
(a) 1 unit
(b) 2 units
(c) 4 units
(d) None of these

Question. The area of a sector of a circle with radius 6 cm if angle of the sector is 60° is   
(a) 15, 2/ 3 cm²
(b) 16, 1/ 2 cm²
(c) 18, 6/ 7 cm²
(d) 19, 3/8  cm

Question. A chord AB of a circle of radius 10 cm subtends a right angle at the centre. The area of the minor-sector is [Take p = 3.14]     

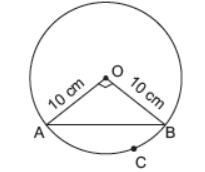
(a) 38.5 cm²
(b) 42 cm2
(c) 78.5 cm²
(d) 82 cm2

Question. In the given figure, PQ = 24 cm, PR = 7 cm and O is the centre of the circle. The area of the shaded portion is   
(a) 132.58 cm²
(b) 148.20 cm²
(c) 154.36 cm²
(d) 161.54 cm²

Question. A square ABCD is inscribed in a circle of radius 10 units. The area of the circle, not included in the square is (Take π = 3.14)   
(a) 84 cm²
(b) 108 cm²
(c) 114 cm²
(d) 122 cm

Question. The area of an equilateral triangle is 17320.5 cm2. With each vertex as centre, a circle is described with radius equal to half the length of the side of the triangle. The area of the triangle not included in the circles is (Use π = 3.14 and 3 = 1.73205).   
(a) 1620.51 cm²
(b) 1810.25 cm²
(c) 2430.60 cm²
(d) None of these

Question. The area of the circle, the circumference of which is equal to the perimeter of a square of side 11 cm is   
(a) 122 cm²
(b) 144 cm²
(c) 154 cm²
(d) 180 cm²

Question. A wheel has diameter 84 cm. Number of complete revolutions must it make to cover 792 metres will be   
(a) 100
(b) 160
(c) 220
(d) 300

Question. The area of a ring shaped region enclosed between two concentric circles of radii20 cm and 15 cm is   
(a) 330 cm²
(b) 415 cm²
(c) 520 cm²
(d) 550 cm²

Question. The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?   
(a) 2275
(b) 2650
(c) 3815
(d) 4375

Question. The area of the shaded portion in the figure, given below, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre is   
(a) 156.64 cm²
(b) 188.46 cm²
(c) 256.64 cm²
(d) 310.25 cm²

Question. In a circular table cover of radius 32 cm, a design is formed having an equilateral triangle ABC in the middle, as shown below. The area of the design is   
(a) 777.36 cm²
(b) 1888.11 cm²
(c) 2010.54 cm²
(d) None of these

Question. ABCD is a square of side 4 cm. At each corner of the square, a quarter circle of radius 1 cm, and at the centre, a circle of radius 1 cm, are drawn, as shown in the given figure. The area of the shaded region is   
(a) 8.46 cm²
(b) 7.25 cm²
(c) 9.71 cm²
(d) 10.43 cm²

Question. In the given figure, ABCD is a square of side 14 cm. Semicircles are drawn with each side of square as diameter. The area of the shaded region is [Take π = 7/ 22 ]

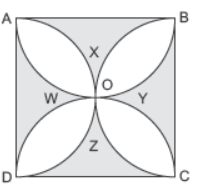
(a) 84 cm²
(b) 96 cm²
(c) 110 cm²
(d) 220 cm²

Question. In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Choose the correct choice as:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
1. Assertion (A): In a circle of radius 6 cm, the angle of a sector is 60°. Then the area of the sector is 18, 6/ 7 cm².
Reason (R): Area of the circle with radius r is πr².
2. Assertion (A): The length of the minute hand of a clock is 7 cm. Then the area swept by the minute hand in 5 minute is 12, 5/ 6 cm².
Reason (R): The length of an arc of a sector of angle q and radius r is given by l = θ / 360 ° × 2πr .