MCQ Chapter 1 Real Numbers Class 10 Mathematics

Please refer to Real Numbers MCQ Questions Class 10 Mathematics below. These MCQ questions for Class 10 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Real Numbers will help you to prepare for the exams and get more marks.

Real Numbers MCQ Questions Class 10 Mathematics

Please see solved MCQ Questions for Real Numbers in Class 10 Mathematics. All questions and answers have been prepared by expert faculty of standard 10 based on the latest examination guidelines.

MCQ Questions Class 10 Mathematics Real Numbers

Question. Which of the following is a pair of co-primes ?
(a) (16, 62)
(b) (18, 25)
(3) (21, 35)
(d) (23, 92)

Question. If x: Every whole number is a natural number and y: 0 is not a natural number, Then which of the following statement is true?
(a) x is false and y is the correct explanation of x.
(b) x is true and y is the correct explanation of x.
(3) x is true and y is false.
(d) Both x and y are true.

Question. The remainder when 7⁸⁴ is divided by 3⁴² is
(a) 0
(b) 1
(3) 49
(d) 341

Question. If a = 1/ 3−2√2 , b = 1/ 3+ 2√2 then the value of a² + b² is
(a) 34
(b) 35
(3) 36
(d) 37

Question. 8 − 8 ×2,1/5 – 1,2/7/2-1/6-1/6 is equal to
(a) 6
(b) 2
(3) 4
(d) 8

Question. The rational form of 2.74¯35 is
(a) 27161/ 9999
(b) 27/ 99
(3) 27161/ 9900
(d) 27161/ 9000

Question. If √3 -1/ √3 + 1 = a + b√3 , then the value of ‘a’ and ‘b’ is
(a) a = 2, b = − 1
(b) a = 2, b = 1
(3) a = − 2, b = 1
(d) a = − 2, b = − 1

Question. The HCF of two numbers, obtained in three steps of division, is 7 and the first 3 quotients are 2,4 and 6 respectively. Find the numbers.
(a) 175, 392
(b) 189, 392
(3) 168, 385
(d) None

Question. The L.C.M. of 2³ × 3² × 5 × 11, 2⁴ × 3⁴ × 5² × 7 and 2⁵ × 3³ × 5³ × 7² × 11 is
(a) 2³ × 3² × 5
(b) 2⁵ × 3⁴ × 5³
(3) 2³ × 3² × 5 × 7 × 11
(d) 2⁵ × 3⁴ × 5³ × 7² x 11

Question. Find the greatest four digit number which when divided by 18 and 12 leaves a remainder of 4 in each case
(a) 9976
(b) 9940
(3) 9904
(d) 9868

Question. The value of 1/√3 +√ 2−1 + on simplifying upto 3 decimal places, given that √2 = 1.4142 and √6 = 2.4495 is
(a) 0.166
(b) 0.366
(3) 0.466
(d) 0.566

Question. The decimal expansion of the rational number 43/ 2⁴ 5³ will terminate after how many places of decimals?   
(a) 2 places
(b) 3 places
(c) 4 places
(d) 5 places

Question. The decimal expansions (without actual division) and its nature (terminating or nonterminating) of 987 10500 will be   
(a) 0.094 __ , non-terminating
(b) 0.094, terminating
(c) 0.094, non-terminating
(d) 0.049, terminating

Question. Rational number between 2 and 3 is     
(a) 1.5
(b) 1.6
(c) 1.7
(d) All of these

Question. If x = 7 + 4√3 + , then the value of x² +1/ x² is
(a) 193
(b) 194
(3) 195
(d) 196

Question. If x = 7 + 4√3, then the value of √x +1/√x is
(a) 8
(b) 6
(3) 5
(d) 4

Question. π is
(a) Rational
(b) Irrational
(3) Imaginary
(d) An integer

Question. The following are the first and last steps in finding the H.C.F. of 408 and 1032 using Euclid’s algorithm.   
Step 1: 1032 = 408X2 + 216
Step 2: ___________
Step 3: ___________
Step 4: 192 = 24 X 8+0
Choose the steps 2 and 3.
(i) 408=2161+1921
(ii) 408=216+180+12
(iii) 216 =192 1 + 24
(iv) 192 = 24 8 + 0
(a) (i) and (ii)
(b) (i) and (iii)
(c) (ii) and (iii)
(d) (iii) and (iv)

Question. By what number must 1789 be divided to get a quotient 29 and remainder 49?     
(a) 60
(b) 61
(c) 59
(d) 52

Question. Given a = 3- √2 . and b = 3+√2 , which of the following is correct?     
(a) a + b is irrational.
(b) a – b is rational.
(c) ab is rational.
(d) a/b is rational.

Question. What is the L.C.M. of 6/14 and 2/7 ?     
(a) 3/7
(b) 6/7
(c) 4/7
(d) 5/7

Question. In a school, the duration of a period in junior section is 40 minutes and in senior section is 60 minutes. If the first bell for each section rings at 9 a.m., when will the two bells ring together again?     
(a) 10:45 a.m.
(b) 10:15 a.m.
(c) 12:00 p.m.
(d) 11:00 a.m.

Question. Which of the following is true for two coprime numbers?     
(a) Their H.C.F. is 1.
(b) TheirL.CM.is1.
(c) Their H.C.F. is equal to their product.
(d) Their L.C.M. is twice their H.C.F.

Question. A circular field has a circumference of 360 km. Two cyclists Sumeet and John start together and cycle at speeds of 12 km/hr and 15 km/hr respectively, a round the circular field. After how many hours will they meet again at the starting point?     
(a) 100 hours
(b) 171 hours
(c) 120 hours
(d) 140 hours

Question. For what value of ‘x’ does 6″ end with 5?   
(a) 0
(b) 1
(c) 5
(d) Never ends with 5.

Question. The difference of the L.C.M. and H.C.F. of 210 and 55 is expressed as 210 x 6 + 55y. What is the value of 3 y ?     
(a) 361
(b) 19
(c) 55
(d) 6859

Question. M The prime factorization of two numbers are 3² x 7³ x 11 and 3 x 7² x 11³ x 17 . Which of the following is a common factor of the numbers?     
(a) 1683
(b) 5831
(c) 1089
(d) 539

Question. The L.C.M. of two numbers is 39780 and their ratio is 13 : 15 then the numbers are
(a) 273,315
(b) 2652,3
(3) 516, 685
(d) none

Question. The L.C.M. of two numbers is 14 times of their H.C.F. The sum of L.C.M. and H.C.F. is 600. If one of the number is 80, then other is
(a) 280
(b) 218
(3) 25
(d) 45

Question. An irrational number is
(a) A terminating and nonrepeating decimal
(b) A nonterminating and nonrepeating decimal
(3) A terminating and repeating decimal
(d) A nonterminating and repeating decimal

Question. Which of the following statement is true ?
(a) Every point on the number line represents a rational number
(b) Irrational numbers cannot be represented by points on the number line
(3) 22/ 7 is a rational number
(d) None of these

Question. 0.¯230.¯22 + = ?
(a) 0.45
(b) 0.43
(3) 0.45
(d) 0.45

Question. 0.0¯18 can be expressed in the rational form as
(a) 18/ 1000
(b) 18/ 990
(3) 18/ 9900
(d) 18/ 999

Question. The equivalent rational form of 17.¯6 is
(a) 53 /3
(b) 88/ 5
(3) 44 /25
(d) None of these

Question. 961/ 625 is a
(a) Terminating decimal
(b) Nonterminating decimal
(3) Cannot be determined
(d) None of these

Question. When simplified, the product (1−1/3)(1−1/4))(1−1/5)……(1−1/n) equals ;
(a) 1/ n
(b) 2/ n
(3) 2(n−1)/ n 
(d) 2/ n(n+1)

Question. Which of the following has most number of divisors ?
(a) 99
(b) 101
(3) 176
(d) 182

Question. A number n is said to be perfect if the sum of all its divisors (excluding n itself) is equal to n. An example of perfect number is
(a) 6
(b) 9
(3) 15
(d) 21

Question. The H.C.F. of 2² × 3³ × 5⁵, 2³ × 3² × 5² × 7 and 2⁴ × 3⁴ × 5 × 7² × 11 is
(a) 2² × 3² × 5
(b) 2² × 3² × 5 × 7 × 11
(3) 2⁴ × 3⁴ × 5⁵
(d) 2⁴ × 3⁴ × 5⁵ × 7 × 11

Question. The sum of rational and irrational number is always
(a) Rational
(b) Irrational
(3) Both
(d) Can’t say

Question. The product of rational and irrational number is always
(a) Rational
(b) Irrational
(3) Both
(d) Can’t say

Question. The least number which should be added to 2497 so that the sum is exactly divisible by 5, 6, 4 and 3 is
(a) 3
(b) 13
(3) 23
(d) 33

Question. The smallest number by which 3600 can be divided to make it a perfect cube is
(a) 9
(b) 50
(3) 300
(d) 450

Question. The least number which is a perfect square and is divisible by each of the numbers 16, 20 and 24, is
(a) 1600
(b) 3600
(3) 6400
(d) 14400

Question. Rational number between √2 and √3 is
(a) √2 +√3/2
(b) √2 X √3 /2 ´
(3) 1.5
(d) 1.8

Question. The number 5 − √5/ 5 +√ 5 is
(a) Rational
(b) Irrational
(3) Both
(d) Can’t say

Question. The largest four-digit number which when divided by 4, 7 or 13 leaves a remainder of 3 in each case, is
(a) 8739
(b) 9831
(c) 9834
(d) 9893

Question. For P ∈ N, 3^4P – 2^4P  is always divisible by ____  
(a) 15
(b) 5
(c) 13
(d) Both
(b) and (c)

Question. If A =14 + (1x 2 x 3 x 4 x 5 …………….A x 10 and B = 19+ (1 x 2 x 3 x 4 x 5 …………….10 x 19) then which one of the following is/are correct?   
(i) B – A is a prime number.
(ii) B + A is a composite number.
(iii) A is a composite number.
(iv) B is a prime number.
(a) Both (i) and (ii)
(b) Both (ii) and (iii)
(c) Both (iii) and (iv)
(d) All (i), (ii), (iii) and (iv)
(e) None of these

Question. The greatest number of 5 digits exactly divisible by 15, 24 and 36 is ____   
(a) 99620
(b) 99720
(c) 99968
(d) 99960
(e) None of these

Question. The greatest number of 6 digits exactly divisible by all the numbers between 1 and 10 (both inclusive) is _________   
(a) 997920  
(b) 999768
(c) 999660
(d) 999760
(e) None of these

Question. The smallest number, which when increased by 19 is exactly divisible by both 2079 and 1404, is _______   
(a) 6200
(b) 625
(c) 6218
(d) 3208
(e) None of these

Question. Without actually performing the Song division, choose which among the following rational numbers will not have a terminating decimal expansion.     
(a) 123/16
(b) 351/2⁷ x 5⁸ x 7¹⁸
(c) 32/28 x 59
(d) 833/49 x 2⁷
(e) None of these

Question. √7 + 4√3/2 equals to ________     
(a) √2 + √6
(b) 2√2 + √6/2
(c) √2 + √6/2
(d) √3 + 2/4
(e) None of these

Question. The largest number that divides 588, 1999 and 1650 leaving 3, 10 and 12 respectively is ______   
(a) 117
(b) 109
(c) 27
(d) 43
(e) None of these

Question. If LCM and HCF of two numbers are equal, then the numbers will be _________         
(a) Composite
(b) Prime
(c) Equal
(d) Co-prime
(e) None of these

Question. The sum of LCM and HCF of two numbers is 29610. If their LCM is 140 times v the HCF of the numbers then which among the following can be one of the numbers?   
(a) 330
(b) 1470
(c) 525
(d) 462
(e) None of these

Question. The least multiple of 7, which leaves a remainder of 4, when divided by 6, 9, 15 and 18 is
(a) 74
(b) 94
(3) 184
(d) 364

Question. The least number, which when divided by 48, 60, 72, 108 and 140 leaves 38, 50, 62, 98 and 130 as remainders respectively, is
(a) 11115
(b) 15110
(3) 15120
(d) 15210

Question. Find the least multiple of 23, which when divided by 18, 21 and 24 leaves remainders 7, 10 and 13 respectively.
(a) 3002
(b) 3013
(3) 3024
(d) 3036

Question. The largest number which divides 133 and 245 leaving a remainder 5 is
(a) 17
(b) 15
(3) 8
(d) 16

Question. The least number which when divided by 5, 6, 7 and 8 leaves a remainder 3, but when divided by 9 leaves no remainder, is
(a) 1677
(b) 1683
(3) 2523
(d) 3363

Question. The H.C.F,. of two numbers is 1/ 5 of their L.C.M. If the product of two number is 720, then the H.C.F. of the numbers is
(a) 13
(b) 12
(3) 14
(d) 18

Question. Four bells begin to toll together and toll respectively at intervals of 5, 6, 8 and 12 seconds. How many times will they toll together in an hour excluding the one at the start
(a) 30
(b) 19
(3) 13
(d) 5

Question. Two ropes of length 28 m and 36 m are to be cut into bits of same length. The greatest possible length of each is
(a) 7
(b) 3
(3) 4
(d) 5

Question. 28 mango trees, 42 apple trees and 21 orange trees have to be planted in rows such that each row contains the same number of trees of one variety only. The minimum number of rows in which the above trees may be planted
(a) 13
(b) 12
(3) 11
(d) 10

Question. A heap is to be formed with lots of 8, 10 and 15 pebbles of different colours. The smallest number of pebbles in the heap is
(a) 121
(b) 120
(3) 110
(d) 8

Question. The smallest number which when diminished by 7, is divisible by 12, 16, 18, 21 and 28 is
(a) 1008
(b) 1015
(3) 1022
(d) 1032

Question. The least number which when increased by 5 is divisible by each one of 24, 32, 36 and 54, is
(a) 427
(b) 859
(3) 869
(d) 4320

Question. The least number, which when divided by 12, 15, 20 and 54 leaves in each case a remainder of 8, is
(a) 504
(b) 536
(3) 544
(d) 548

Question. Three measuring tapes are 64 cm, 72 cm, 96 cm, the shortest length that can measured by any one of the tapes exactly is
(a) 576
(b) 120
(3) 8
(d) 10.

Question. The L.C.M. of two numbers is 48. The numbers are in the ratio 2 : 3. The sum of the numbers is
(a) 28
(b) 32
(3) 40
(d) 64

Question. The value of [(x^a−a−1)1/^a−1]^a/a+1 =
(a) x
(b) 1/x
(3) x^a
(d) 1/x^a

Question. If a = 2 +√3/ 2−√3 , b = 2−√3/ 2 +√3 , then the value of a + b is
(a) 14
(b) −14
(3) 8 √3
(d) − √3

Question. The product of two numbers is 960. If H.C.F. is 8, then the numbers are
(a) 24,40
(b) 8, 120 or 24, 40
(3) 8, 140
(d) none of these

Question. (x^a+b)²(x^b+c)²(x^c+a)²/(xa.xb.xc)⁴ 
(a) −1
(b) 0
(3) 1
(d) None

Question. 2ⁿ⁺⁴ −2(b)n/2(2ⁿ⁺³) +2⁻³ is equal to
(a) 2ⁿ⁺¹
(b) −2ⁿ⁺¹ + 1/ 8
(3) 9/8−2ⁿ 
(d) 1

Question. The least number divisible by 12, 15, 20, and is perfect square is
(a) 900
(b) 400
(3) 36
(d) 256

Question. The HCF of 405, 840 and 960 is     
(a) 9
(b) 15
(c) 45
(d) none of these

Question. Which of the following number is rational :     
(a) √2 + 3
(b) (7 − √5) (7 +√5)
(c) 3/√5
(d) ( √3 − √7)²

Question. 1/7 , when expressed as a non-terminating and recurring decimal is given by :       
(a) 0.142857
(b) 0.428571
(c) 0.857142
(d) none of these

Question. Which of the following number have a terminating decimal representation :   
(a) 7/ 80
(b) 3/ 345
(c) 8/ 17
(d) 5/ 224

Question. The product of three consecutive positive integers is always divisible by :     
(a) 4
(b) 5
(c) 6
(d) 12

Question. The largest number which divides 615 and 963 leaving remainder 6 in each case is :     
(a) 29
(b) 87
(c) 116
(d) none of these

Question. Which of the following number do not have a terminating decimal representation :     
(a) 7/ 50
(b) 19/ 1000
(c) 12 /105
(d) 113 /2500

Question. The HCF of the smallest composite number and the smallest prime number is         
(a) 1
(b) 2
(c) 3
(d) 5

Question. Four bells toll at an interval of 8, 12, 15 and 18 seconds respectively. All the four begin to toll together. The number of times they toll together in one hour excluding the one at the start will be       
(a) 5
(b) 8
(c) 10
(d) 12

Question. On a morning walk, three persons step off together and their steps measure 40 cm, 42 cm and 45 cm, respectively. The minimum distance each should walk so that each can cover the same distance in complete steps is 
(a) 1260 cm
(b) 1920 cm
(c) 2242 cm
(d) 2520 cm

Question. The values of A and B in the following factor tree, respectively are   

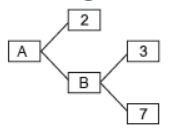
(a) 42, 21
(b) 21, 42
(c) 12, 10
(d) 10, 12

Question. [HCF × LCM] for the numbers 100 and 190 is       
(a) 190
(b) 1900
(c) 19000
(d) None of these

Question. When 2120 is expressed as the product of its prime factors we get   

(a) 2 × 5³ × 53
(b) 2³ × 5 × 53
(c) 5 × 7² × 31
(d) 5² × 7 × 33

Question. The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then the other number is     
(a) 20
(b) 28
(c) 60
(d) 80

Question. The HCF of 657and 963 is :     
(a) 3
(b) 6
(c) 9
(d) none of these

Very Short Answer and Question :

Question. Which number should be multiplied to ( √7 −√5) to get a rational number?   

Question. Express 0.2545454…………..as a fraction in simplest form.   

Question. The decimal expansion of the rational no.43/2⁴5³ will terminate after how many places of decimal?  

Question. Write a rational number between √2 and √3 .    

Question. Write one rational and one irrational number lying between 0.25 and 0.32.   

Question. Find the HCF of 65&117 and express it in the form of 65m+117n. 

Question. Find the HCF and LCM of 6,72 and 120 using the prime factorization method.   

Question. Find the LCM & HCF of 26 and 91 and verify that HCF x LCM=product of the two numbers. 

Question. Check whether 6n can end with the digit 0, where n is any natural number.   

Question. Write down the decimal expansion of 7 / 80 .  

Question. If HCF (72, 120) = 24, then what is the LCM (72, 120) ? 

Question. How many prime factors are there in the prime factorisation of 420.   

Question. Express 156 as a product of its prime factors. 

Question. If LCM (24, 80) = 240, then what is the HCF (24, 80)?