Please refer to Statistics MCQ Questions Class 10 Mathematics below. These MCQ questions for Class 10 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Statistics will help you to prepare for the exams and get more marks.
Statistics MCQ Questions Class 10 Mathematics
Please see solved MCQ Questions for Statistics in Class 10 Mathematics. All questions and answers have been prepared by expert faculty of standard 10 based on the latest examination guidelines.
MCQ Questions Class 10 Mathematics Statistics
Question. For the following distribution the modal class is

(a) 50 – 60
(b) 40 – 50
(c) 20 – 30
(d) 30 – 40
Answer
D
Question. The mean of 25 observations is 36. If the mean of first 13 observations is 32 and that of the last 13 observations is 39, then the 13th observation is
(a) 13
(b) 23
(c) 32
(d) 36
Answer
B
Question. To represent ‘the more than type’ graphically, we plot the ____________ on the x – axis.
(a) class marks
(b) lower limits
(c) upper limits
(d) class size
Answer
B
Question. If ∑ƒ;X;=1860 and ∑ ƒ;= 30, then the value of ¯x is
(a) 26
(b) 63
(c) 64
(d) 62
Answer
D
Question. The mean of the first 10 natural numbers is
(a) 4.5
(b) 5
(c) 6
(d) 5.5
Answer
D
Question. The wickets taken by a bowler in 10 cricket matches are 2, 6, 4, 5, 0, 2, 1, 3, 2, 3. The median of the data is
(a) 2.5
(b) 1
(c) 2
(d) 3
Answer
A
Question. The measure of central tendency that can be obtained graphically is
(a) none of these
(b) median
(c) mode
(d) mean
Answer
B
Question. In the given data if n = 230, l = 40, cf = 76, h = 10, f = 65, then its median is
(a) 48
(b) 40
(c) 47
(d) 46
Answer
D
Question. The marks obtained by 9 students in Mathematics are 59, 46, 30, 23, 27, 44, 52, 40 and 29. The median of the data is
(a) 35
(b) 29
(c) 30
(d) 40
Answer
D
Question. To represent ‘the less than type’ graphically, we plot the ________ on the x – axis.
(a) class marks
(b) class size
(c) lower limits
(d) upper limits
Answer
D
Question. Upperclasslimit + Lowerclasslimit /2 = .
(a) frequency
(b) Class mark
(c) None of these
(d) class size
Answer
B
Question. The times, in seconds, taken by 75 athletes to run a 500m race are tabulated as below:

The number of athletes who completed the race in less than 125 seconds is
(a) 20
(b) 17
(c) 18
(d) 27
Answer
D
Question. In a data, if l = 40, h = 15, f1= 7, f0 = 3, f2 = 6, then the mode is
(a) 82
(b) 62
(c) 52
(d) 72
Answer
C
Question. The mean of the first 10 prime numbers is
(a) 129
(b) 1.29
(c) 12.9
(d) 11.9
Answer
C
Question. The mean of the first 10 natural odd numbers is
(a) 9
(b) 12
(c) 11
(d) 10
Answer
D
Question. For the following distribution

the sum of lower limits of the median class and modal class is
(a) 190
(b) 20
(c) 180
(d) 170
Answer
D
Question. The mean of ‘n’ observations is . If the first item is increased by 1, second by 2 and so on, then the new mean is
(a) ¯x −n−1/2
(b) ¯x−n+1/2
(c) ¯x+n+1/2
(d) ¯x
Answer
C
Question. The arithmetic mean of a set of 40 values is 65. If each of the 40 values is increased by 5, what will be the mean of the set of new values:
(a) 65
(b) 60
(c) 70
(d) 50
Answer
C
Question. The most frequent value in the data is known as
(a) mean
(b) mode
(c) all the three
(d) median
Answer
B
Question. If x ; are the midpoints of the class intervals of grouped data ƒ; are the corresponding frequencies and ¯x is the mean, then ∑(ƒ;x; −¯x) is equal to
(a) 2
(b) 0
(c) -1
(d) 1
Answer
B
Question. The marks obtained by 9 students in Mathematics are 59, 46, 30, 23, 27, 40, 52, 35 and 29. The median of the data is
(a) 29
(b) 35
(c) 40
(d) 30
Answer
B
Question. The median of first 10 prime numbers is
(a) 12.5
(b) 13
(c) 11
(d) 12
Answer
D
Question. Mode + 2/3 (Mean −Mode ) =.
(a) Mode
(b) Median
(c) Mean
(d) None of these
Answer
B
Question. Construction of cumulative frequency table is useful to determine
(a) mean
(b) all the three
(c) median
(d) mode
Answer
C
Question. The empirical relationship between the three measures of central tendencies is
(a) 3 mode = mean + 2 median
(b) Mode= 3 median – 2 mean
(c) 3 mean = median + 2 mode
(d) None of these
Answer
B
One Word Questions :
Question. Find the mean of first five natural numbers.
Answer
3
Question. The mean of 20 numbers is 17. If 3 is added to every number, then find the new mean.
Answer
20
Question. If ¯x is the mean of n obeservations x1,x2,. . . . . . . . , xn then find n ∑i=i (xi – ¯x) .
Answer
0
Question. If 27 is taken out from the given data then what is the new median?
20, 24, 25, 26, 27, 28, 29, 30
Answer
26
Question. When 93 is added to the data given below what is the new median?
43, 47, 51, 53, 67, 79, 84, 97
Answer
67
Question. Find the mean of first five prime numbers.
Answer
5.6
Question. The mean of 6, 4, 7, x and 14 is 8. Find x.
Answer
9
Question. Find the frequencies of the data:-
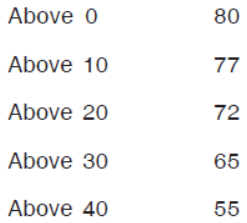
Answer
3, 5, 7, 10
Question. The mean of 5 numbers is 18. If one number is excluded their mean is 16. Find the excluded number .
Answer
26
Question. In the following data what is Σfi ?

Answer
23 + p
Question. What is the mean of n numbers x1,x2, . . . . . . . . . .xn ?
Answer
∑xi/n
Question. Find the sum of deviations of the variate values 3, 4 ,6, 8, 14 from their mean.
Answer
0
Question. What is the mode of the given data?
2, 2, 3, 5, 5, 7, 7, 2, 3, 4, 7, 2
Answer
2
Question. Find the value of x if the mode of the data is 18.
16, 18, 17, 16, 18, x, 19, 17, 14
Answer
18
Question. What is the value of x if the median of given data is 27.5?
24, 25, 26, x + 2, x + 3, 30, 31, 34
Answer
x = 25
Question. If ui = xi – 25 /10 , ∑fi ui = 20 and ∑fi = 100 then find the value of ¯x .
Answer
27
Question. The mean of 20 numbers is 35. If each number is divided by 5 then what is the new mean.
Answer
7
Question. What is the mean of data x, x + 2, x + 4, x + 6, x + 8 ?
Answer
x + 4
Question. Find the median of the numbers :–
7, 8, 9, 11, 13, 14, 15, 16
Answer
12
Question Find the mean of first five odd natural numbers.
Answer
5
Question. What is the mode of the given data?
2, 2, 3, 5, 5, 7, 7, 2, 3, 4, 7, 2
Answer
2
Question. Find the value of x if the mode of the data is 18.
16, 18, 17, 16, 18, x, 19, 17, 14
Answer
18
Question. The scores of two batsmen A and B in five innings of a test series are 18
What is the mean score of batsman B?
Answer
52
Question. If mode of the data (given) is 43 then what is the value of x + 2?
34, 43, 48, 43, x, 48, 60, 64
Answer
45
Question. What is the mean of first five composite numbers?
Answer
7.4
Question. Find the frequencies:-

Answer
5, 4, 8, 12, 16
Question. Find the missing frequency p if Σfi = 30 and

Answer
8
Question. In the following data what is fixi ?

Answer
235 + 10p
Question. The number of children of 10 families of a locality are 2, 4, 3, 4, 2, 0, 3, 5, 1, 1. What is the mean number of children per family?
Answer
2.5
Question. What is the median of numbers:-
16, 17, 18, 20, 21, 24, 25, 26, 28?
Answer
21
Question. For the numbers 9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9 find 7
Answer
0
Question. The mean of 40 observations was 160.It was detected on rechecking that the value of 165 was wrongly copied as 125 for computing of mean. Find the correct mean.
Answer
161
Question. What is the mean of observations x1,x2, . . . . . . . . . .xn with frequencies f1, f2, . . . . . . ,fn?
Answer
∑xi fi/∑fi
Question. What is the mean of the data 6, 8, 7, 3, 2?
Answer
5.2
Question. In a factory the daily wages of 5 workers are 20, 40, 42, 45 and 33. If the daily wages of each worker is increased by Rs. 5, find the mean wage.
Answer
41



