Please refer to Class 12 Mathematics Sample Paper Term 1 Set D with solutions below. The following CBSE Sample Paper for Class 12 Mathematics has been prepared as per the latest pattern and examination guidelines issued by CBSE. By practicing the Mathematics Sample Paper for Class 12 students will be able to improve their understanding of the subject and get more marks.
CBSE Class 12 Mathematics Sample Paper for Term 1
Section A
In this section, attempt any 16 questions out of Questions 1-20. Each question is of 1 mark weightage.
1. If matrix A given by A=

then the order of the matrix A is
(a) 1 x 2
(b) 2 x 3
(c) 3 x 2
(d) 2 x 2
Answer
C
2. The minimum value of the function f (x) = x – 4 exists at
(a) x = 0
(b) x = 2
(c) x = 4
(d) x = – 4
Answer
C
3. The domain of sec-1 x is
(a) R -[-1, 1]
(b) R
(c) [- 1, 1]
(d) None of these
Answer
D
4. The region represent by the inequation system x, y ≥ 0, y ≤ 5 and x + y ≤ 2 is
(a) unbounded in Ist quadrant
(b) unbounded in Ist and IInd quadrants
(c) bounded in Ist quadrant
(d) None of these
Answer
C
5. The value of
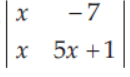
at x = – 1 is
(a) – 1
(b) – 3
(c) 2
(d) – 5
Answer
B
6. The function f given by f (x) = 3x + 17, is
(a) strictly increasing on R
(b) strictly decreasing on R
(c) decreasing on R
(d) Both (b) and (c) are correct
Answer
A
7. Maximise Z =10x + 5y subject to constraints x ≤ 4, y ≤ 6 and x, y ≥ 0.
(a) 40 at (0,0)
(b) 40 at (4,0)
(c) 70 at (4, 6)
(d) 30 at (0, 6)
Answer
C
8. The value of

(a) 0
(b) 1
(c) 2
(d) 3
Answer
B
9. A vertex of a feasible region by the linear constraints 2x + y ≤ 30, x + 2y ≤ 24 and x, y ≥ 0 is
(a) (0, 10)
(b) (12, 6)
(c) (0,2)
(d) (14, 0)
Answer
B
10. If
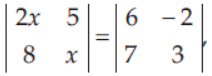
then value of x/6 is
(a) – 5
(b) ± 1
(c) ± 6
(d) 0
Answer
B
11. The value of determinant
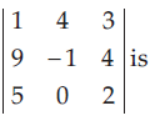
(a) 21
(b) 166
(c) 64
(d) None of these
Answer
A
12. The feasible solution for a LPP is shown in following figure. Let Z = 2x – 3y be the objective function. (Maximum Value of Z +Minimum Value of Z) is equal to

(a) 0
(b) – 2
(c) – 1
(d) – 3
Answer
D
13. The function f (x) = x2 – x4 , x ∈[0, 4] attains minimum value at
(a) x = 0
(b) x = 1
(c) x = 2
(d) x = 4
Answer
C
14. If A is 3 x 3matrix such that A = 10 , then 3A equals
(a) 270
(b) 240
(c) 72
(d) 216
Answer
A
15. The range of cosec -1x is
(a) [-π/2 , π/2]
(b) ]-π/2 , π/2[
(c) [-π/2 , π/2] – {0}
(d) None of these
Answer
C
16. The domain in which sine function will be one-one, is
(a) [-π/2 , π/2]
(b) [π/2 , 3π/2]
(c) [0, π]
(d) Both (a) and (b)
Answer
D
17. If Radha has 15 notebooks and 6 pens, Fauzia has 10 notebooks and 2 pens and Simran has 13 notebooks and 5 pens, then the above information is expressed as

(a) Only by I
(b) Only by II
(c) Both I and II
(d) None of these
Answer
C
18. If

then the values of x, y, z, a, b and c are
(a) x = – 3, y = – 5, z = 2, a = – 2, b= – 7 and c = – 1
(b) x = – 2, y = – 7, z = – 1, a = – 3, b = – 5 and c = 2
(c) x = – 3, y = – 5, z = 2, a = 2, b = 7 and c =1
(d) x = 3, y = 5, z = 2, a = 2, b = 7 and c = 1
Answer
A
19. If A is a matrix defined by A = [aij ] = [sinjx i]; 1 ≤ i ≤ 3, 1 ≤ j ≤ 3 and B is a matrix defined by B = [bij ] = [cos i x j]; 1 ≤ i ≤ 3, 1 ≤ j ≤ 3.
Then, the value of a22/b12 is
(a) 2 cos x2
(b) 2 sin x2
(c) 2 sin x2
(d) None of these
Answer
C
20. The value of Δ =
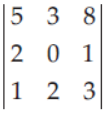
using cofactors of elements of second row is
(a) -14
(b) 14
(c) -7
(d) 7
Answer
D
Section B
In this section, attempt any 16 questions out of Questions 21-40. Each question is of 1 mark weightage.
21. If f(x) = √4+x-2/x , ≠ 0 be continuous at x = 0, then 4 f (0) is equal to
(a) 1/2
(b) 1/4
(c) 1
(d) 3/2
Answer
C
22. If
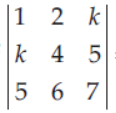
=0 , then the possible values of k are
(a) -3 and 3
(b) -3 and -8/3
(c) -3 and -1/3
(d) 3 and 8/3
Answer
D
23. The least value of f(x) = ex + e-x is
(a) -2
(b) 2
(c) 0
(d) 1
Answer
B
24. The points on the curve x 2 + y2 – 2x – 3 = 0 at which the tangents are parallel to the X-axis, are
(a) (1, ± 2)
(b) (1, ± 3)
(c) (2, ± 2)
(d) None of these
Answer
A
25. Which of the following statements is true for f (x) = 4x3 – 6x2 – 72x + 30 ?
I. f is strictly increasing in the interval (- ∞, – 2).
II. f is strictly increasing in the interval (3, ∞).
III. f is strictly decreasing in the interval (- 2, 3).
IV. f is neither increasing nor decreasing in R.
(a) I and Il are true
(b) II and III are true
(c) II and IV are true
(d) All are true
Answer
D
26. Let f(x) = In (1+ax) – In (1-bx)/x , x ≠ 0. If f (x) is continuous at x = 0, then f (0) – a – b is equal to
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
27. All the points of discontinuity of f defined by f (x) =|x|-|x + 1|is/are
(a) 0, 1
(b) 1, 0, 2
(c) no point of discontinuity
(d) None of these
Answer
C
28. Secant function is bijective when its domain and range are ..A.. and R – (-1, 1) respectively. Here, A refers to
(a) [0,π]
(b) [0,π/2]
(c) [0,π] – {π/2}
(d) None of these
Answer
C
29. The domain of the function y = sin-1(-x2) is
(a) [0, 1]
(b) [0,1]
(c) [-1, 1]
(d) φ
Answer
C
30. Which of the following is true?
(a) tan tan -1 = 1 1
(b) tan1 tan 1 > -1
(c) tan1 tan 1 < -1
(d) None of these
Answer
B
31. The function f (x) = 4 sin3 x – 6 sin2 x + 12 sin x + 100 is strictly
(a) increasing in (π , 3π/2)
(b) decreasing in (π/2 ,π)
(c) decreasing in [-π/2 ,π/2]
(d) decreasing in [0,π/2]
Answer
B
32. The interval in which y = x2 e-x is increasing, is
(a) (- ∞, ∞)
(b) (-2,0)
(c) (2, ∞)
(d) (0, 2)
Answer
D
33. Derivative of log [log (log x5 )] w.r.t. x is
(a) 1/x log x . log(log x5)
(b) 1/x log x (logx5)
(c) 5/x log (logx5)
(d) None of these
Answer
A
34. If y = log(x2/1+x2) , then dy/dx is equal to
(a) 1/x(1+x2)
(b) 2x/1+x2
(c) 2/x(1+x2)
(d) x/(1+x2)
Answer
C
35. If area of triangle is 4 sq units with vertices (-2, 0), (0, 4) and (0, k), then k is equal to
(a) 0 and -8
(b) 8
(c) -8
(d) 0 and 8
Answer
D
36. The equation of the tangent to the curve y = √4x + 5, which is parallel to the line 2x – y + 3 = 0, is
(a) 2x – y +3 = 0
(b) x – y +3 = 0
(c) 2x + y +3 = 0
(d) x -2y +3 = 0
Answer
A
37. The equations of the tangent and normal to the parabola y2 =4ax at the point (at2 , 2at) are respectively
(a) ty = x + at2 and y = – tx + 2at + at3
(b) ty = x – at2 and y = tx – 2at + at3
(c) y = tx + 2at + at3 and ty = x + at2
(d) y = – tx + 2at + at3 and ty = x + at2
Answer
A
38. If x = a (cos θ + θ sin θ) and y = a(sinq – θ cosθ), then dy/dx is equal to
(a) tan θ
(b) cot θ
(c) sin θ
(d) cos θ
Answer
A
39. The value of y – x from the equation 2
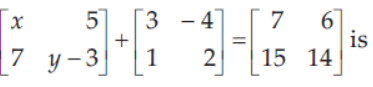
(a) – 5
(b) 5
(c) – 7
(d) 7
Answer
D
40. If Z = 2x + 3y, subject to constraints x + 2y ≤ 10, 2x + y ≤ 14 and x, y ³ 0, then one of the corner point of feasible region is
(a) (0, 7)
(b) (6, 2)
(c) (5, 0)
(d) (8, 1)
Answer
B
Section C
In this section, attempt any 8 questions. Each question is of 1 mark weightage. Questions 46-50 are based on Case-Study.
41. The maximum value of the objective function, Z = 34x + 45y Subject to constraints x + y ≤ 300, 2x + 3y ≤ 70 and x, y ≥ 0, is
(a) 1190
(b) 1100
(c) 1150
(d) 1290
Answer
A
42. If y = √(x-1)(x-2)/x-3 , then dy/dx is equal to
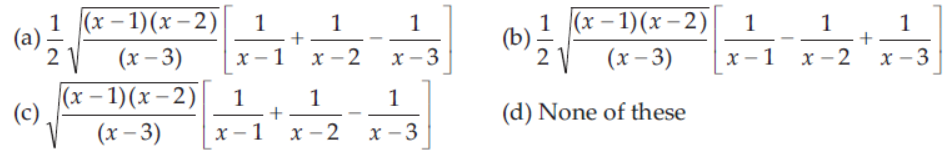
Answer
D
43. The function f(x) =

is continuous at x = π/2 , when k equals
(a) -6
(b) 6
(c) 5
(d) -5
Answer
B
44. If f (x) =
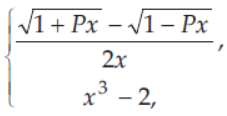
is continuous at x = 0, then P is equal to
(a) -4
(b) -3
(c) -2
(d) -1
Answer
A
45. If 2x + 3y =
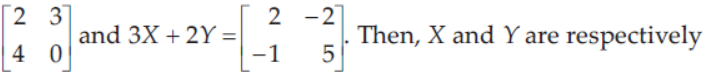
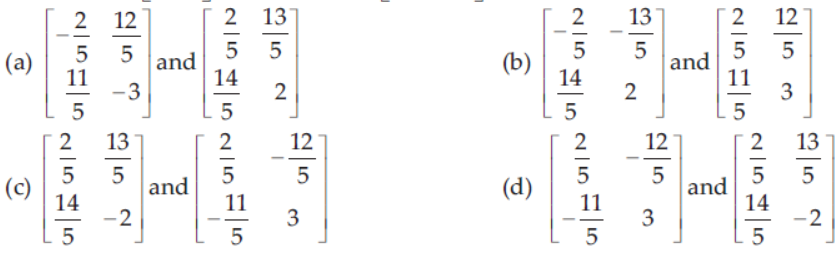
Answer
D
CASE STUDY
A relation R in a set Ais called:
Reflexive, if (a, a) ∈ R, for every a∈ A.
Symmetric, if (a1 , a2 ) R ∈ , implies that (a2 , a1 ) R ∈ , for all a1, a2 ∈ A
Transitive, if (a1, a2) ∈ R and (a2, a3) ∈ R implies that (a1, a3) ∈ R for all a1, a2, a3 ∈ A.
Based on the above information, answer the following questions.
46. If R = {(a, b) : a and b work at the same place}, then R is
(a) reflexive
(b) symmetric
(c) transitive
(d) an equivalence relation
Answer
D
47. If R ={(x, y): x is father of y}, then R is
(a) reflexive but not symmetric
(b) symmetric and transitive
(c) neither reflexive nor symmetric nor transitive
(d) symmetric but not reflexive
Answer
C
48. Let R be the relation in the set A of all books in a library of a college given by R = {{x, y): x and y have same number of pages}. Then, R is
(a) not reflexive
(b) not symmetric
(c) not transitive
(d) an equivalence relation
Answer
D
49. If R = {(x, y): x is exactly 7cm taller than y}, then R is
(a) not symmetric
(b) reflexive
(c) symmetric but not transitive
(d) an equivalence relation
Answer
A
50. The relation R in the set A = {1, 2, 3} given by R = {(1,2), (2, 1)} is
(a) reflexive
(b) symmetric
(c) transitive
(d) reflexive and symmetric
Answer
B
