Please refer to Relations and Functions MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Relations and Functions will help you to prepare for the exams and get more marks.
Relations and Functions MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Relations and Functions in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Relations and Functions
Question. let R be the relation in the set N given by R={(a,b):a=b-2,b>6}.Choose the correct answer.
(a) (2,4)€R
(b) (3,8) € R
(c) (6,8)€ R
(d) (8,10) € R
Answer
D
Question:
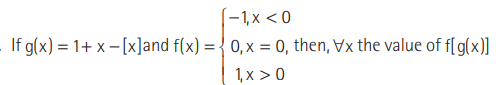
is
(a) x
(b) 1
(c) f (x )
(d) g (x)
Answer
B
Question: f : [-3π,2π] →[-1,1] defined by f (x) sin = 3x is
(a) into
(b) onto
(c) one one
(d) None of these
Answer
B
Question: If f = {( 5,2 ), (6, 3)} and g = {(2,5 ), ( 3,6 )}, then the range of f and g respectively.
(a) (5,3) and (2, 3)
(b) (5, 6) and (3,2)
(c) (2,3) and (5,6)
(d) (2,3) and (6,5)
Answer
C
Question: Let A = {0,1,2,3} and define a relation R on A as follows R = {(0,0), (0,1), (0,3), (1 ,0), (1,1), (2,2), (3,0), (3,3), then R is
(a) reflexive and symmetric
(b) symmetric and transitive
(c) reflexive and transitive
(d) a equivalence relation
Answer
A
Question: Relation R in set N of natural numbers defined as R {(x ,y) :y=x+5 and x < 4} are
(a) reflexive
(b) symmetric
(c) not reflexive not symmetric
(d) not reflexive not symmetric not transitive
Answer
D
Question: Let R be a relation on the set N of natural numbers defined by nRm, if n divides m. Then, R is
(a) reflexive and symmetric
(b) transitive and symmetric
(c) equivalence
(d) reflexive, transitive but not symmetric
Answer
D
Question: Relation R in the set Z of all integers defined as R={( x, y ) :x-y is an integer} is/are
(a) reflexive and symmetric
(b) only transitive
(c) symmetric but not transitive
(d) an equivalence relation
Answer
D
Question: Relation R in the set A = {1,2,3,4,5,6} as R={(x ,y) :y is divisible by x} are
(a) reflexive and transitive
(b) reflexive and symmetric
(c) symmetric and transitive
(d) None of the above
Answer
A
Question: The relation R in R defined by R ={(a ,b ):≤b3} is
(a) reflexive
(b) symmetric
(c) transitive
(d) None of these
Answer
D
Question. Let T be the set of all triangles in the Euclidean plane, and let a relation R on T be defined as aRb if a is congruent to b ∀ a, b ∈ T. Then R is
(a) reflexive but not transitive
(b) transitive but not symmetric
(c) equivalence
(d) None of these
Answer
C
Question. Let S = {1, 2, 3, 4, 5} and let A = S × S. Define the relation R on A as follows: (a, b) R (c, d) iff ad = cb. Then, R is
(a) reflexive only
(b) Symmetric only
(c) Transitive only
(d) Equivalence relation
Answer
D
Question. Let f: R → R is defined as f(x) = 3x then f is
(a) f is one-one and onto
(b) f is one-one but not onto
(c) f is many-one
(d) f is neither one-one nor onto
Answer
A
Question. If f : R → R defined by f (x) = 2x-7/4 is an invertible function, then f –1 is equal to
(a) (4x+5)/2
(b) (4x+7)/2
(c) 3x+2/2
(d) 9x+3/5
Answer
B
Question. Let A = {1, 2, 3} and B = {a, b, c}, then the number of bijective functions from A to B are
(a) 2
(b) 8
(c) 6
(d) 4
Answer
C
Question. Consider the function f in A = R – {2/3} defined as f (x) = 4x+3/6x-4 , then f –1 is equal to
(a) 3+4x/6x-4
(b) 6x-4/3+4x
(c) 3-4x/6x-4
(d) 9+2x/6x-4
Answer
A
Question. If the binary operation x on the set of integers Z, is defined by a x b = a + 3b2, then the value of 8 x 3 is
(a) 32
(b) 40
(c) 36
(d) 35
Answer
D
Question. Consider the non-empty set consisting of children in a family and a relation R defined as a R b if a is brother of b. Then R is
(a) symmetric but not transitive
(b) transitive but not symmetric
(c) neither symmetric nor transitive
(d) both symmetric and transitive
Answer
B
Question. Let us define a relation R in R as aRb if a ≥ b. Then R is
(a) an equivalence relation
(b) reflexive, transitive but not symmetric
(c) symmetric, transitive but not reflexive
(d) neither transitive nor reflexive but symmetric
Answer
D
Question. Let f : R → R be defined by f(x) = 1/x ∀ ∈ R . Then f is
(a) one-one
(b) onto
(c) bijective
(d) f is not defined
Answer
D
Question. Let f : R → R be defined by f(x) = 3x2 – 5 and g : R → R by g(x) = x/x2+1 . Then gof is
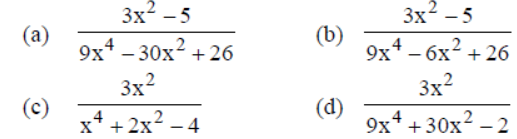
Answer
A
Question. Let f(x) = 2x2, g(x) = 3x + 2 and fog (x) = 18 x2 + 24x + c, then c =
(a) 2
(b) 8
(c) 6
(d) 4
Answer
B
Question. If f(x) = |x| and g(x) = |5x – 2|, then
(a) gof (x) = |5x – 2|
(b) gof (x) = |5| x | – 2|
(c) fog (x) = |5| x | – 2|
(d) fog (x) = |5x + 2|
Answer
B
Question. Let A = {1, 2, 3, 4} and let R = {(2, 2), (3, 3), (4, 4), (1, 2)} be a relation on A. Then R is:
(a) reflexive
(b) symmetric
(c) transitive
(d) None of these
Answer
C
Question. If R is a relation in a set A such that (a, a)∈ R for every a ∈ A, then the relation R is called
(a) symmetric
(b) reflexive
(c) transitive
(d) symmetric or transitive
Answer
B
Question. Let f : R → R be defined as f (x) = 2x3. then
(a) f is one-one onto
(b) f is one-one but not onto
(c) f is onto but not one-one
(d) f is neither one-one nor onto
Answer
A
Question. If f : R → R is given by f (x) =√1-x2 , then fof is
(a) √x
(b) x2
(c) x
(d) 1– x2
Answer
C
Question. If f is an even function and g is an odd function, then the function fog is
(a) an even function
(b) an odd function
(c) neither even nor odd
(d) a periodic function
Answer
B
Question. If f : R → R be a mapping defined by f(x) = x3 + 5, then f–1(x) is equal to:
(a) (x + 3)1/3
(b) (x – 5)1/3
(c) (5 – x)1/3
(d) (5 – x)
Answer
B
Question. The relation “less than” in the set of natural numbers is :
(a) only symmetric
(b) only transitive
(c) only reflexive
(d) equivalence relation
Answer
B
Question. Let f : R → R be defined as f(x) = x2+1/2 , then
(a) f is one-one onto
(b) f is one-one but not onto
(c) f is onto but not one-one
(d) f is neither one-one nor onto
Answer
D
Question. A relation R in a set A is called empty relation, if
(a) no element of A is related to any element of A
(b) every element of A is related to every element of A
(c) some elements of A are related to some elements of A
(d) None of the above
Answer
A
Question. If f (x) is defined on [0, 1] by the rule
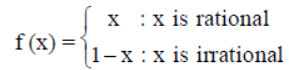
then for all x ∈ R, f (f(x)) is
(a) constant
(b) 1 + x
(c) x
(d) None of these
Answer
C
Question. A relation R in a set A is said to be an equivalence relation, if R is
(a) symmetric only
(b) reflexive only
(c) transitive only
(d) All of these
Answer
D
Question. If N be the set of all natural numbers, consider f : N → N such that f(x) = 2x, ∀ x ∈ N, then f is
(a) one-one onto
(b) one-one into
(c) many-one onto
(d) None of these
Answer
B
Question. Let A = {1, 2, 3} and R = {(1, 2), (2, 3)} be a relation in A.
Then, the minimum number of ordered pairs may be added, so that R becomes an equivalence relation, is
(a) 7
(b) 5
(c) 1
(d) 4
Answer
A
Question. Let f(x) = ax-b/cx+d . Then fof (x) = x provided that
(a) d = – a
(b) d = a
(c) a = b = c = d = 1
(d) a = b = 1
Answer
A
Question. If f (x) = sin x + cos x, g (x) = x2 – 1, then g (f (x)) is invertible in the domain
(a) [0,π/2]
(b) [-π/4 , π/4]
(c) [-π/2 , π/2]
(d) [0, π]
Answer
B
Question. Let g(x) = x2 – 4x – 5, then
(a) g is one-one on R
(b) g is not one-one on R
(c) g is bijective on R
(d) None of these
Answer
B
Question. A function f from the set of natural numbers to integers defined by

(a) neither one-one nor onto
(b) one-one but not onto
(c) onto but not one-one
(d) one-one and onto both
Answer
D
Question. Given f (x) = log(1+x/1-x) and g(x) = 3x+x3/1+3x2 , then fog(x) equals
(a) – f (x)
(b) 3f(x)
(c) [f (x)]3
(d) None of these
Answer
B
Question. If R = {(x, y) : x is father of y}, then R is
(a) reflexive but not symmetric
(b) symmetric and transitive
(c) neither reflexive nor symmetric nor transitive
(d) Symmetric but not reflexive
Answer
C
Question. Let P = {(x, y) l x2 + y2 = 1, x, y ∈ R}. Then, P is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Anti-symmetric
Answer
B
Question. Set A has 3 elements and set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer
C
Question. Let R be a relation on the set N of natural numbers denoted by nRm⇔ n is a factor of m (i.e. n | m). Then, R is
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric
Answer
D
Question. A Relation from A to B is an arbitrary subset of:
(a) AxB
(b) BxB
(c) AxA
(d) BxB
Answer
A
Question. Set A has 3 elements and the set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is
(a) 144
(b) 12
(c) 24
(d) 64
Answer
C
Question. The maximum number of equivalence relations on the set A = {1, 2, 3} are
(a) 1
(b) 2
(c) 3
(d) 5
Answer
D
Question. Let A = {x : -1 ≤ x ≤ 1} and f : A → A is a function defined by f(x) = x |x| then f is
(a) a bijection
(b) injection but not surjection
(c) surjection but not injection
(d) neither injection nor surjection
Answer
A
Question. Let R be a relation on set of lines as L1 R L2 if L1 is perpendicular to L2. Then
(a) R is Reflexive
(b) R is transitive
(c) R is symmetric
(d) R is an equivalence relation
Answer
C
Question. Let X = {-1, 0, 1}, Y = {0, 2} and a function f : X → Y defined by y = 2×4, is
(a) one-one onto
(b) one-one into
(c) many-one onto
(d) many-one into
Answer
C
Question. Let R be a relation on the set L of lines defined by l1 R l2 if l1 is perpendicular to l2, then relation R is
(a) reflexive and symmetric
(b) symmetric and transitive
(c) equivalence relation
(d) symmetric
Answer
D
Read Assertion and reason carefully and write correct option for each question
(a) Both A and R are correct; R is the correct explanation of A.
(b) Both A and R are correct; R is not the correct explanation of A.
(c) A is correct; R is incorrect.
(d) R is correct; A is incorrect.
Question. Assertion (A)The relation R in the set {1, 2, 3} given by R = {(1, 1), (2, 2),(3, 3), (1, 2), (2, 3)} is reflexive but neither symmetric nor transitive.
Reason (R)R is not symmetric, as (1, 2) ∈R but (2, 1) ∉R. Similarly, R is not transitive, as (1, 2) ∈R and (2, 3) ∈R
but (1, 3) ∉R.
Answer
A
Question. Assertion (A) Let R be the relation defined in the set A = {1, 2, 3, 4, 5, 6, 7} by R = {(a, b) : both a and b are either odd or even}. R is an equivalence relation
Reason (R) Since R is reflexive, symmetric but R is not transitive.
Answer
C
Question. Assertion (A) The Modulus Function f :R→R, given by f (x) = | x | is not one one and onto function
Reason (R) The Modulus Function f :R→R, given by f (x) = | x | is bijective function
Answer
C
Question. Assertion (A) Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function From A to B. Then f is one-one.
Reason (R) Since the function f : N→N, given by f (x) = 2x, is not onto
Answer
B
Question. Assertion (A)The relation R in the set Z of integers given by R = {(a, b) : 2 divides a – b} is reflexive and symmetric
Reason (R)R is reflexive, as 2 divides (a – a) for all a ∈Z.
Answer
B
Question. Assertion (A)A function f : X →Y is said to be one-one and onto (or bijective)
Reason (R) if f is both one-one and onto.
Answer
A
Question. Assertion (A) The relation R in R defined as R = {(a, b) :a≤b} is not equivalence relation.
Reason (R) Since R is not reflexive but it is symmetric and transitive.
Answer
C
Question. Assertion (A) Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Then f is one-one.
Reason (R) f is bijective function
Answer
C
Question. Assertion (A) Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y) 😡 and y have same number of pages} is not equivalence relation.
Reason (R) Since R is reflexive, symmetric and transitive.
Answer
C
Question. Assertion (A) A one-one function f : {1, 2, 3} →{1, 2, 3} must be onto.
Reason (R) Since f is one-one, three elements of {1, 2, 3} must be taken to 3 different elements of the co- domain {1, 2, 3} under f.
Answer
A


