Please refer to Vector Algebra MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Vector Algebra will help you to prepare for the exams and get more marks.
Vector Algebra MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Vector Algebra in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Vector Algebra
Question. The perpendicular distance of A(1, 4, –2) from BC, where coordinates of B and C are respectively (2, 1, –2) and (0, –5, 1) is
(a) 3/7
(b) √26/7
(c) 3/√26/7
(d) √26
Answer
C
Question. If two vectors a and b represented by two adjacent sides of a parallelogram in magnitude and direction then a + b is represented as
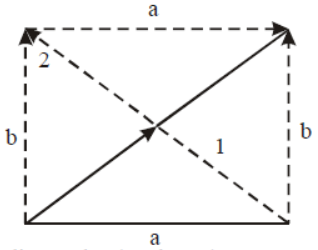
(a) diagonal 1 (as shown)
(b) diagonal 2 (as shown)
(c) sides opposite to either of the side
(d) None of the above
Answer
A
Question. If l, m and n are the direction cosines of a vector, and α, β and γ are the angles which the vector makes with X, Y and Z-axes respectively, then the unit vector in the direction of that vector is
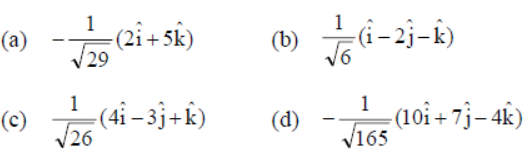
Answer
B
Question. Which of the following is an example of two different vectors with same magnitude?
(a) (2î +3ĵ + k̂) and (2î +3ĵ – k̂)
(b) (3î + 5ĵ + k̂) and (3î + 4ĵ + k̂)
(c) (ĵ + k̂) and (2ĵ + 3k̂)
(d) None of the above
Answer
A
Question.
Answer
B
Question. ABCD be a parallelogram and M be the point of intersection of the diagonals, if O is any point, then OA + OB + OC + OD is equal to
(a) 3 OM
(b) 2 OM
(c) 4 OM
(d) OM
Answer
C
Question. Let a̅ , b̅ , c̅ be three vectors of magnitudes 3, 4 and 5 respectively. If each one is perpendicular to the sum of the other two vectors, then | a̅ + b̅ + c̅ | =
(a) 5
(b) 3 √2
(c) 5 √2
(d) 12
Answer
C
Question. If position vector of a point A is a̅ + 2b̅ and any point P(a̅) divides A̅B̅ in the ratio of 2 : 3, then position vector of B is
(a) 2 a̅ -b̅
(b) b̅ – 2a̅
(c) a̅ -3b̅
(d) b̅
Answer
C
Question. Which of the following is true?
(a) î.î = ĵ.ĵ = k̂.k̂ = 0
(b) î.ĵ = ĵ.k̂= k̂.î = 0
(c) Both (a) and (b) are true
(d) Both (a) and (b) are not true
Answer
D
Question. Multiplication of two vectors is defined in two ways, namely
(a) scalar product and dot product
(b) vector product and cross product
(c) scalar product and vector product
(d) None of the above
Answer
C
Question. Consider points A, B, C and D with position vectors 7î – 4ĵ + 7k̂ , î – 6ĵ + 10k̂ , -î – 3ĵ + 4k̂ and 5î – ĵ + 5k̂ respectively. Then ABCD is a
(a) parallelogram but not a rhombus
(b) square
(c) rhombus
(d) None of these
Answer
D
Question. A unit vector in xy- plane makes an angle of 45° with the vector î + ĵ and an angle of 60° with the vector 3î – 4ĵ is

Answer
C
Question. The three vectors î + ĵ , ĵ + k̂ , k̂+ î taken two at a time form three planes. The three unit vectors drawn perpendicular to these three planes form a parallelopiped of volume :
(a) 1/3
(b) 4
(c) 3√3/4
(d) 4/3√3
Answer
D
Question. Let a̅ , b̅ , c̅ be unit vectors such that a̅ + b̅ + c̅ = o̅ . Which one of the following is correct ?
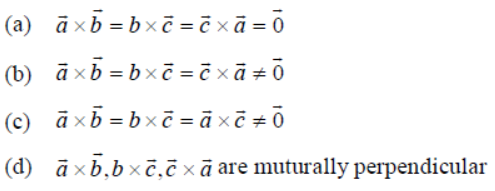
Answer
B
Question. If a̅ is perpendicular to

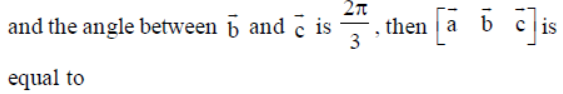
(a) 4 √3
(b) 6 √3
(c) 12 √3
(d) 18 √3
Answer
C
Question. If a = 2î + ĵ + 3k̂ , b = -î + 2ĵ + k̂ and c = 3î + ĵ + 2k̂ then a.(b × c) is equal to
(a) – 15
(b) 15
(c) – 10
(d) – 5
Answer
C
Question. Which of the following statement is correct?
(a) a.(b x c) = [b c a]
(b) [a b c] = [c a b]
(c) [c a b] = c.(a x b) = (a x b).c
(d) All are correct
Answer
D
Question. Which of the following is correct?
(a) [a b c] = [a c b]
(b) [a c b] = 0
(c) Both (a) and (b) are correct
(d) Both (a) and (b) are incorrect
Answer
A
Question. The altitude through vertex C of a triangle ABC, with position vectors of vertices a̅, b̅, c̅, respectively is :
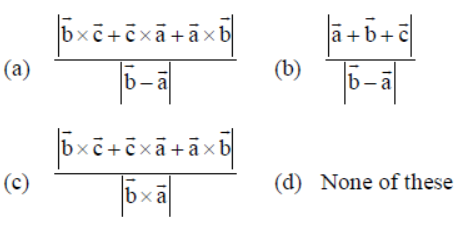
Answer
A
Question. The two vectors

(a) for no real value of x
(b) for x = –1
(c) for x = 1/2
(d) for x = – 1/2 and x = 1
Answer
D
Question. If θ is the angle between any two vectors a and b, then |a.b| = a x b| , where θ is equal to
(a) zero
(b) π/4
(c) π/2
(d) π
Answer
B
Question.

(a) π/3
(b) π/2
(c) π/6
(d) π/4
Answer
A
Question.
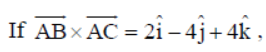
then the area of ΔABC is
(a) 3 sq. units
(b) 4 sq. units
(c) 16 sq. units
(d) 9 sq. units
Answer
A
Question. If a is a vector of magnitude 50, collinear with the vector b = 6î – 8ĵ – 15/2 k̂ and makes an acute angle with the positive direction of Z-axis, then a is equal to

Answer
A
Question. The vectors
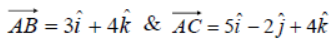
are the sides of a triangle ABC. The length of the median through A is
(a) √288
(b) √18
(c) √72
(d) √33
Answer
D
Question. If a̅ , b̅, c̅ are mutually perpendicular unit-vector, then |a̅ + b̅ + c̅| equals :
(a) 1
(b) √2
(c) √3
(d) 2
Answer
C
Question.
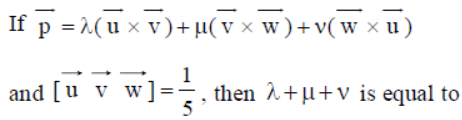
(a) 5
(b) 10
(c) 15
(d) None of these
Answer
D
Question. If |a̅ | = 3, |b̅ | = 4 , then a value of λ for which a̅ + λ b̅ is perpendicular to a̅ – λb̅ is :
(a) 9/16
(b) 3/4
(c) 3/2
(d) 4/3
Answer
B
Question. Which one of the following statement is not correct ?
(a) Vector product is commutative
(b) Vector product is not associative
(c) Vector product is distributive over addition
(d) Scalar product is commutative
Answer
A
Question. ABCDEF is a regular hexagon where centre O is the origin.
If the position vectors of A and B are î – ĵ + 2k̂ and 2î + ĵ – k̂ respectively, then B̅C̅ is equal to
(a) î + ĵ – 2k̂
(b) -î + ĵ – 2k̂
(c) 3î + 3ĵ – 4k̂
(d) None of these
Answer
B
Question. Three points (2, –1, 3), (3, –5, 1) and (– 1, 11, 9) are
(a) Non-collinear
(b) Non-coplanar
(c) Collinear
(d) None of these
Answer
C
Question. If p, q, r be three non-zero vectors, then equation p .q = p . r implies:
(a) q = r
(b) p is orthogonal to both q and r.
(c) p is orthogonal to q – r.
(d) either q = r or p is perpendicular to q – r.
Answer
D
Question. If a̅ , b̅, c̅ are vectors such that [a̅ b̅ c̅] = 4, then [a̅ x b̅ b̅ x c̅ c̅ x a̅] =
(a) 16
(b) 64
(c) 4
(d) 8
Answer
A
Question. | (a × b).c| = |a| |b||c| , if
(a) a.b = b. c = 0
(b) b.c = c. a = 0
(c) c.a = a.b = 0
(d) a.b = b.c = c.a = 0
Answer
D
Question. If C is the middle point of AB and P is any point outside AB, then
(a) P̅A̅ + P̅B̅ + = P̅C̅
(b) P̅A̅ + P̅B̅ + = 2P̅C̅
(c) P̅A̅ + P̅B̅ + = P̅C̅ = O̅
(d) P̅A̅ + P̅B̅ + = 2P̅C̅ = O̅
Answer
B
Question. If unit vector c̅ makes an angle π/3 with î + ĵ , then minimum and maximum values of (î x ĵ) .c̅ respectively are
(a) 0, √3/2
(b) -√3/2 , √3/2
(c) -1 , √3/2
(d) None of these
Answer
B
Question. If ABCDE is a pentagon, then resultant of AB, AE, BC, DC, ED and AC is
(a) 2AC
(b) 3AC
(c) AB
(d) None of these
Answer
B
Question. The non-zero vectors a, b and c are related by a = 8b and c = – 7b, then the angle between a and c is
(a) π
(b) 0
(c) π/4
(d) π/2
Answer
A
Question. For any two vectors a and b, (a × b)2 equals
(a) a2b2 – (a.b)2
(b) a2 + b2
(c) a2 – b2
(d) None of these
Answer
A
Question. The dot product of a vector with the vectors î + ĵ – 3k̂, î + 3ĵ – 2k̂and 2î + ĵ -4k̂ are 0, 5 and 8 respectively. Find the vector.
(a) î + 2ĵ + k̂
(b) -î + 3ĵ + 2k̂
(c) î + 2ĵ + 3k̂
(d) î – 3ĵ – 3k̂
Answer
A

