Please refer to Linear Programming MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Linear Programming will help you to prepare for the exams and get more marks.
Linear Programming MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Linear Programming in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Linear Programming
Question. If a point (h, k) satisfies an inequation ax + by ≥ 4, then the half plane represented by the inequation is
(a) The half plane containing the point (h, k) but excluding the points on ax + by = 4
(b) The half plane containing the point (h, k) and the points on ax + by = 4
(c) Whole xy-plane
(d) None of these
Answer
B
Question. Z = 6x + 21y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4, 0)
(b) (28, 8)
(c) (2 , 1/2)
(d) (0, 3)
Answer
C
Question. The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20).
Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is
(a) p = q
(b) p = 2 q
(c) q = 2 p
(d) q = 3 p
Answer
D
Question. The lines 5x + 4y ≥ 20, x ≤ 6, y ≤ 4 form
(a) A square
(b) A rhombus
(c) A triangle
(d) A quadrilateral
Answer
D
Question. Shaded region is represented by
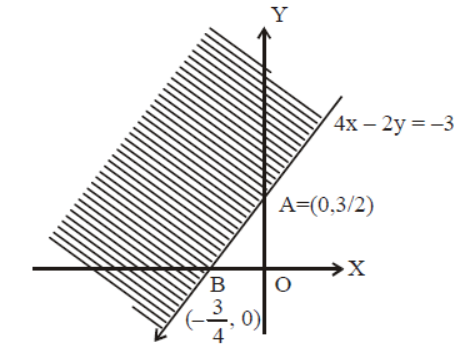
(a) 4x – 2y ≤3
(b) 4x – 2y ≤–3
(c) 4x – 2y ≥3
(d) 4x – 2y ≥–3
Answer
D
Question. Inequation y – x ≤ 0 represents
(a) The half plane that contains the positive X-axis
(b) Closed half plane above the line y = x, which contains positive Y-axis
(c) Half plane that contains the negative X-axis
(d) None of these
Answer
A
Question. Objective function of a L.P.P. is
(a) a constant
(b) a function to be optimised
(c) a relation between the variables
(d) None of these
Answer
B
Question. Corner points of the feasible region for an LPP are (0, 2) (3, 0) (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function.
The minimum value of F occurs at
(a) (0, 2) only
(b) (3, 0) only
(c) the mid-point of the line segment joining the points (0, 2) and (3, 0) only
(d) any point on the line segment joining the points (0, 2) and (3, 0)
Answer
D
Question. The feasible region for an LPP is shown shaded in the figure.
Let Z = 3 x – 4 y be the objective function. Minimum of Z occurs at
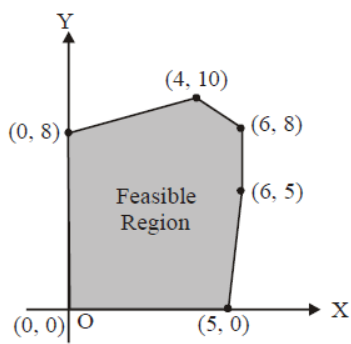
(a) (0, 0)
(b) (0, 8)
(c) (5, 0)
(d) (4, 10)
Answer
B
Question. The maximum value of P = x + 3y such that 2x + y ≤ 20, x + 2y ≤ 20, x ≥0, y ≥0 is
(a) 10
(b) 60
(c) 30
(d) None of these
Answer
C
Question. The maximum value of z = 2x + 5y subject to the constraints 2x + 5y ≤ 10, x + 2y ≥1, x – y ≤ 4, x ≥ y ≥ 0, occurs at
(a) exactly one point
(b) exactly two points
(c) infinitely many points
(d) None of these
Answer
C
Question. The feasible solution of a L.P.P. belongs to
(a) Only first quadrant
(b) First and third quadrant
(c) Second quadrant
(d) Any quadrant
Answer
D
Question. Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0, is
(a) 16 at (4,0)
(b) 24 at (0, 4)
(c) 24 at (6, 0)
(d) 36 at (0, 6)
Answer
D
Question. Shamli wants to invest `50,000 in saving certificates and PPE. She wants to invest atleast `15,000 in saving certificates and at least `20,000 in PPF. The rate of interest on saving certificates is 8% p.a. and that on PPF is 9% p.a.
Formulation of the above problem as LPP to determine maximum yearly income, is
(a) Maximize Z = 0.08x + 0.09y Subject to, x + y ≤ 50,000, x ≥ 15000, y ≥ 20,000
(b) Maximize Z = 0.08x + 0.09y Subject to, x + y ≤ 50,000, x ≥ 15000, y ≤ 20,000
(c) Maximize Z = 0.08x + 0.09y Subject to, x + y ≤ 50,000, x ≤ 15000, y ≥ 20,000
(d) Maximize Z = 0.08x + 0.09y Subject to, x + y ≤ 50,000, x ≤ 15000, y ≤ 20,000
Answer
A
Question. A furniture manufacturer produces tables and bookshelves made up of wood and steel. The weekly requirement of wood and steel is given as below.

The weekly variability of wood and steel is 450 and 100 units respectively. Profit on a table ₹1000 and that on a bookshelf is ₹1200. To determine the number of tables and bookshelves to be produced every week in order to maximize the total profit, formulation of the problem as L.P.P. is
(a) Maximize Z = 1000x + 1200 y Subject to 8x + 11y ≥ 450, 2x + 3y ≤ 100, x ≥ 0, y ≥ 0
(b) Maximize Z = 1000x + 1200 y Subject to 8x + 11y ≤ 450, 2x + 3y ≤ 100, x ≥ 0, y ≥ 0
(c) Maximize Z = 1000x + 1200 y Subject to 8x + 11y ≤ 450, 2x + 3y ≥ 100, x ≥ 0, y ≥ 0
(d) Maximize Z = 1000x + 1200 y Subject to 8x + 11y ≥ 450, 2x + 3y ≥ 100, x ≥ 0, y ≥ 0
Answer
B
Question. A company manufactures two types of products A and B.
The storage capacity of its godown is 100 units. Total investment amount is ₹ 30,000. The cost price of A and B are ₹ 400 and ₹ 900 respectively. Suppose all the products have sold and per unit profit is ₹ 100 and ₹ 120 through A and B respectively. If x units of A and y units of B be produced, then two linear constraints and iso-profit line are respectively
(a) x + y =100; 4x + 9y = 300, 100x + 120y = c
(b) x + y ≤100; 4x + 9y ≤ 300, x + 2y = c
(c) x + y ≤100; 4x + 9y ≤ 300,100x +120y = c
(d) x + y ≤100; 9x + 4y ≤ 300, x + 2y = c
Answer
C
Question. For the constraint of a linear optimizing function z = x1 + x2, given by x1+ x2 ≤1, 3×1+ x2 ≥ 3 and x1, x2 ≥ 0,
(a) There are two feasible regions
(b) There are infinite feasible regions
(c) There is no feasible region
(d) None of these.
Answer
C
Question. The optimal value of the objective function is attained at the points
(a) Given by intersection of inequations with axes only
(b) Given by intersection of inequations with x- axis only
(c) Given by corner points of the feasible region
(d) None of these.
Answer
C
Question. Feasible region for an LPP is shown shaded in the following figure. Minimum of Z = 4 x + 3 y occurs at the point.
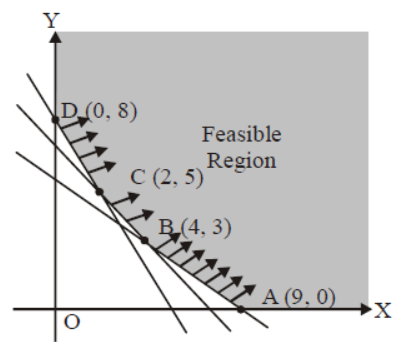
(a) (0, 8)
(b) (2, 5)
(c) (4, 3)
(d) (9, 0)
Answer
B
Question. Which of the following cannot be considered as the objective function of a linear programming problem?
(a) Maximize z = 3x + 2y
(b) Minimize z = 6x + 7y + 9z
(c) Maximize z = 2x
(d) Minimize z = x2 + 2xy + y2
Answer
D
Question. The number of corner points of the L.P.P.
Max Z = 20x + 3y subject to the constraints x + y ≤ 5, 2x + 3y ≤ 12, x ≥ 0, y ≥ 0 are
(a) 4
(b) 3
(c) 2
(d) 1
Answer
A
Question. Graph of the inequalities x ≥ 0, y ≥ 0, 2x + 3y ≥ 6, 3x + 2y ≥ 6 is
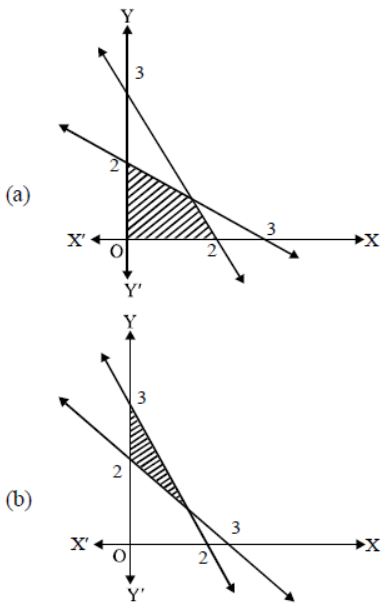
Answer
C
Question. A printing company prints two types of magazines A and B.
The company earns `10 and `15 on each magazine A and B respectively. These are processed on three machines I, II & III and total time in hours available per week on each machine is as follows: 56
The number of constraints is
(a) 3
(b) 4
(c) 5
(d) 6
Answer
C
Question. The maximum value of z = 4x + 2y subject to constraints 2x + 3y ≤ 18, x + y ≥10 and x, y ≥ 0, is
(a) 36
(b) 40
(c) 20
(d) None
Answer
D
Question. The solution set of the following system of inequations: x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥1, is
(a) bounded region
(b) unbounded region
(c) only one point
(d) empty set
Answer
D
Question. A linear programming of linear functions deals with
(a) Minimizing
(b) Optimizing
(c) Maximizing
(d) None of these
Answer
B
Question. The maximum value of P = x + 3y such that 2x + y ≤ 20, x + 2y ≤ 20, x ≥0, y ≥0 is
(a) 10
(b) 60
(c) 30
(d) None
Answer
C
Question. Region represented by x ≥ 0, y ≥ 0 is
(a) first quadrant
(b) second quadrant
(c) third quadrant
(d) fourth quadrant
Answer
A
Question. The maximum value of z = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24 and x ≥ 0, y ≥ 0 is
(a) 90
(b) 120
(c) 96
(d) 240
Answer
B
Question. A wholesale merchant wants to start the business of cereal with ₹ 24000. Wheat is ₹ 400 per quintal and rice is ₹ 600 per quintal. He has capacity to store 200 quintal cereal. He earns the profit ₹ 25 per quintal on wheat and ₹ 40 per quintal on rice. If he store x quintal rice and y quintal wheat, then for maximum profit, the objective function is
(a) 25 x + 40 y
(b) 40x + 25 y
(c) 400x + 600y
(d) 400/40 x + 600/5 y
Answer
B
Question. Graph of the constraints x/3 + y/4 ≤1, x ≥ 0, y 0 is


Answer
B
Question. The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is
(a) 10
(b) 26
(c) 35
(d) 70
Answer
C
Question. L.P.P is a process of finding
(a) Maximum value of objective function
(b) Minimum value of objective function
(c) Optimum value of objective function
(d) None of these
Answer
C
Question. Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4 x + 6 y be the objective function.
The minimum value of F occurs at
(a) (0, 2) only
(b) (3, 0) only
(c) the mid point of the line segment joining the points (0, 2) and (3, 0).
(d) any point on the line segment joining the points (0, 2) and (3, 0).
Answer
D
Question. Children have been invited to a birthday party. It is necessary to give them return gifts. For the purpose, it was decided that they would be given pens and pencils in a bag. It was also decided that the number of items in a bag would be atleast 5. If the cost of a pen is `10 and cost of a pencil is `5, minimize the cost of a bag containing pens and pencils. Formulation of LPP for this problem is
(a) Minimize C = 5x + 10y subject to x + y ≤ 10, x ≥ 0, y ≥ 0
(b) Minimize C = 5x + 10y subject to x + y ≥10, x ≥ 0, y ≥ 0
(c) Minimize C = 5x + 10y subject to x + y ≥ 5, x ≥ 0, y ≥ 0
(d) Minimize C = 5x + 10y subject to x + y ≤ 5, x ≥ 0, y ≥ 0
Answer
A
Question. For the following feasible region, the linear constraints are

(a) x ≥ 0, y ≥ 0, 3x + 2y ≥12, x + 3y ≥11
(b) x ≥ 0, y ≥ 0, 3x + 2y ≤12, x + 3y ≥11
(c) x ≥ 0, y ≥ 0, 3x + 2y ≤12, x + 3y ≤11
(d) None of these
Answer
A
Question. The no. of convex polygon formed bounding the feasible region of the L.P.P. Max. Z = 30x + 60y subject to the constraints 5x + 2y ≤ 10, x + y ≤ 4, x ≥ 0, y ≥ 0 are
(a) 2
(b) 3
(c) 4
(d) 1
Answer
D
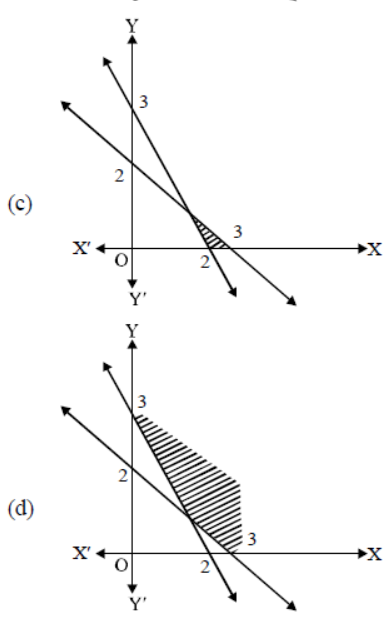
Question. The linear inequations for which the shaded area in the following figure is the solution set, are

(a) x + y ≤ 1, 2x + y ≥ 2, x – 2y ≥ 8, x ≤ 0, y ≥ 0
(b) x – y ≥ 1, 2x + y ≥ 2, x + 2y ≥ 8, x ≥ 0, y ≥ 0
(c) x – y ≤ 1, 2x + y ≥ 2, x + 2y ≤ 8, x ≥ 0, y ≥ 0
(d) x + y ≥ 1, 2x + y ≤ 2, x + 2y ≥ 8, x ≥ 0, y ≥ 0
Answer
C
Question. Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y, ≤ 9, x ≥ 0, y ≥ 0, is
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)
Answer
C
Question. Corner points of feasible region of inequalities gives
(a) optional solution of L.P.P.
(b) objective function
(c) constraints.
(d) linear assumption
Answer
A

