Please refer to Linear Equations MCQ Questions Class 10 Mathematics below. These MCQ questions for Class 10 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Linear Equations will help you to prepare for the exams and get more marks.
Linear Equations MCQ Questions Class 10 Mathematics
Please see solved MCQ Questions for Linear Equations in Class 10 Mathematics. All questions and answers have been prepared by expert faculty of standard 10 based on the latest examination guidelines.
MCQ Questions Class 10 Mathematics Linear Equations
Question. The value of k for which the system of linear equations 3x + y = 1, (2k –1)x + (k –1)y = 2k + 1 have no solution is
(a) k = 2
(b) k = 4
(c) k = 6
(d) k = 8
Answer
A
Question. If a pair of linear equations is consistent, then the line represented by them are
(a) parallel
(b) intersecting or coincident
(c) always coincident
(d) always intersecting
Answer
B
Question. If 2x + 5y – 1 = 0, 2x + 3y – 3 = 0, then
(a) x = 1, y = – 3
(b) x = 3, y = –1
(c) x = 2, y = 5
(d) x = 5, y = – 3
Answer
B
Question. If the equations kx – 2y = 3 and 3x + y = 5 represent two intersecting lines at unique point, then the value of k is
(a) Only 4
(b) Only 5
(c) Only 6
(d) Any number other than –6
Answer
D
Question. The value of k for which the given system has unique solution 2x + 3y – 5 = 0, kx – 6y – 8 = 0 is
(a) k = 2
(b) k ≠ 4
(c) k = 4
(d) k ≠ 4
Answer
D
Question. If 3 – (x – 5) = y + 2, 2(x + y) = 4 – 3y, then
(a) x = 13/ 4 , y = 9 /10
(b) x = 7/ 16 , y = 5 /8
(c) x = 4/ 9 , y = 9/ 12
(d) x = 26/ 3 , y = −8/ 3
Answer
D
Question. For what values of p, the pair of equations 4x + py +8 =0 and 2x +2y +2 = 0 have unique solution?
(a) p = 4
(b) p ≠ 4
(c) p = 7
(d) p ≠ 7
Answer
B
Question. What type of straight lines will be represented by the system of equations 2x + 3y = 5 and 4x + 6y = 7?
(a) Intersecting
(b) Parallel
(c) Conincident
(d) None of these
Answer
B
Question. For what value of p, the following pair of linear equations have infinitely many solutions? (p – 3)x + 3y = p, px + py = 12
(a) 4
(b) 6
(c) 9
(d) 11
Answer
B
Question. If 4/x +3y =8; 6/x -4y =-5 , then
(a) x = 2, y = 2
(b) x = 1, y = –1
(c) x = 2, y = –2
(d) x = 3, y = – 3
Answer
A
Question. The value of k for which the following pair of linear equations have infinitely many solutions: 2x + 3y = 7, (k – 1)x + (k + 2)y = 3k is
(a) 2
(b) 4
(c) 7
(d) 9
Answer
C
Question. The value(s) of k for which the pair of linear equations kx + y = k2 and x + ky = 1 have infinitely many solutions is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question. Solution of the simultaneous linear equations: 2x/y -y/2 =-1/6 and x/2 +2y/3 =3 is
(a) x = 2, y = – 3
(b) x = – 2, y = 3
(c) x = 2, y = 3
(d) x = – 2, y = – 3
Answer
C
Question. The value of x satisfying both the equations 4x – 5 = y and 2x – y = 3, when y = –1 is
(a) 1
(b) –1
(c) 2
(d) –2
Answer
A
Question. Which of the following is not a solution of the pair of equations 3x – 2y = 4 and 6x – 4y = 8?
(a) x = 2, y = 1
(b) x = 4, y = 4
(c) x = 6, y = 7
(d) x = 5, y = 3
Answer
D
Question. If x + 2y – 3 = 0, 3x – 2y + 7 = 0, then
(a) x = –1, y = 2
(b) x = 1, y = 2
(c) x = 2, y = 3
(d) x = – 2, y = – 3
Answer
D
Question. For what value of k, the following system of equations have infinite solutions: 2x – 3y = 7, (k + 2)x – (2k + 1)y = 3 (2k – 1)?
(a) k = 2
(b) k = 3
(c) k = 4
(d) k = 8
Answer
C
Question. The value of m for which the pair of linear equations 2x + 3y – 7 = 0 and (m – 1) x + (m + 1) y = (3m – 1) has infinitely many solutions is
(a) 5
(b) 8
(c) – 5
(d) 8
Answer
A
Question. If 2x + 3y = 11 and 2x – 4y = –24, then the value of ‘m’ for which y = mx + 3 is
(a) 0
(b) 1
(c) –1
(d) – 2
Answer
C
Question. If 2x + 3y = 11 and x – 2y = –12, then the value of ‘m’ for which y = mx + 3 is
(a) 1
(b) –1
(c) 2
(d) – 2
Answer
B
Question. If 7(y + 3) – 2(x + 2) = 14, 4(y – 2) + 3(x – 3) = 2, then
(a) x = 1, y = 4
(b) x = 3, y = 5
(c) x = 5, y = 1
(d) None of these
Answer
C
Question. The pair of linear equations 3x/2 +5y/3 = 7 and 9x + 10y = 14 is
(a) consistent
(b) inconsistent
(c) consistent with one solution
(d) consistent with many solutions
Answer
B
Question. If 2x = 5y + 4, 3x – 2y + 16 = 0, then
(a) x = 2, y = –2
(b) x = 3, y = –3
(c) x = 4, y = 5
(d) x = – 8, y = – 4
Answer
D
Question. The value of k for which the system of equations kx + 4y = k – 4, 16x + ky = k have infinite number of solutions is
(a) k = 2
(b) k = 4
(c) k = 6
(d) k = 8
Answer
D
Question. The value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent is
(a) −14/ 3
(b) 2/ 5
(c) 5
(d) 10
Answer
D
Question. If 4/x +5y =7 ;3/x+4y = 5 , then
(a) x = 1 3 y = –1
(b) x = 8, y = 3
(c) x = 4, y = 7
(d) x = 5, y = 9
Answer
A
Question. The value of k for which the system of equations kx + 4y = k – 4, 16x + ky = k have infinite number of solutions is
(a) k = 2
(b) k = 4
(c) k = 6
(d) k = 8
Answer
D
Question. The solution of given system of equations:
x + y = a + b, ax – by = a2 – b2 is
(a) x = 2a, y = b
(b) x = a, y = 2b
(c) x = a, y = b
(d) x = 1/ a , y = 1/b
Answer
C
Question. In figure, ABCD is a rectangle. The values of x and y, respectively are
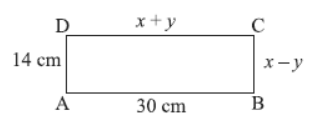
(a) x = 12, y = 16
(b) x = 16, y = 10
(c) x = 22, y = 8
(d) x = 15, y = 18
Answer
C
Question. The solution of the system of equations x + y = 5, x – y = 2 using substitution method is:
(a) x = 7/ 2 , y = 3/ 2
(b) x = 3 /5 , y = 1/ 2
(c) x = 3 /5 , y = 1 /4
(d) x = 2 /5 , y = 5/ 2
Answer
A
Question. When 3x + 2y = 11 3 and –7x + 5y = 313 are solved by elimination method, we get
(a) x = 5 /19 , y =111/ 37
(b) x = 9 /85 , y = 160/ 27
(c) x = −4/ 71 , y = 5/ 28
(d) x = y −7/ 87 ,Y = 170/87
Answer
D
Question. Solving 3x – 5y – 4 = 0 and 9x = 2y + 7 by the elimination method, we get the values of x and y as
(a) x = 9 /13 , y = −5/ 13
(b) x = 11/24 , y = 15/ 23
(c) x =17 / 25 , y =16 / 9
(d) None of these
Answer
A
Question. The value(s) of k for which the pair of linear equations kx + y = k2 and x + ky = 1 have infinitely many solutions is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
A
Question. For what values of p and q, the following pair of linear equations have infinitely many solutions?
4x + 5y = 2; (2p + 7q)x + (p + 8q)y = 2q – p + 1
(a) p = 1, q = 3
(b) p = 3, q = 4
(c) p = –2, q = 5
(d) p = –1, q = 2
Answer
D
Question. If the equations kx – 2y = 3 and 3x + y = 5 represent two intersecting lines at unique point, then the value of k is
(a) Only 4
(b) Only 5
(c) Only 6
(d) Any number other than –6
Answer
D
Question. The values of a and b for which the following pair of linear equations have infinitely many solutions:
2x + 3y = 7, (a + b)x + (2a – b)y = 21, respectively are
(a) a = 5, b = 1
(b) a = 2, b = 3
(c) a = 4, b = 7
(d) None of these
Answer
A
Question. For what value of p, the following pair of linear equations have infinitely many solutions?
(p – 3)x + 3y = p, px + py = 12
(a) 4
(b) 6
(c) 9
(d) 11
Answer
B
Question. For which values of k, the pair of equations kx + 3y = k – 3 and 12x + ky = k have no solution?
(a) k = 2
(b) k = 6
(c) – 6
(d) k = –2
Answer
C
Question. For what value of k, the following system of equations have infinite solutions:
2x – 3y = 7, (k + 2)x – (2k + 1)y = 3 (2k – 1)?
(a) k = 2
(b) k = 3
(c) k = 4
(d) k = 8
Answer
C
Question. The value of k for which the following pair of linear equations have infinitely many solutions:
2x + 3y = 7, (k – 1)x + (k + 2)y = 3k is
(a) 2
(b) 4
(c) 7
(d) 9
Answer
C
Question. The value of p if the lines represented by the equations 3x – y – 5 = 0 and 6x – 2y – p = 0 are parallel is
(a) only 8
(b) only 10
(c) only 15
(d) All values of ‘p’ except 10
Answer
C
Question. The value of m for which the pair of linear equations 2x + 3y – 7 = 0 and (m – 1) x + (m + 1) y = (3m – 1) has infinitely many solutions is
(a) 5
(b) 8
(c) – 5
(d) 8
Answer
A
Question. The pair of linear equations 3x/2 + 5y/3 and 9x + 10y = 14 is
(a) consistent
(b) inconsistent
(c) consistent with one solution
(d) consistent with many solutions
Answer
B
Question. The value of k for which the given system has unique solution 2x + 3y – 5 = 0, kx – 6y – 8 = 0 is
(a) k = 2
(b) k ≠ 4
(c) k = 4
(d) k ≠ 4
Answer
D
Question. For what value of k, the pair of linear equations 3x + y = 3 and 6x + ky = 8 does not have a solution?
(a) 2
(b) –2
(c) 4
(d) –4
Answer
A
Question. For what values of p, the pair of equations 4x + py +8 =0 and 2x +2y +2 = 0 have unique solution?
(a) p = 4
(b) p ≠ 4
(c) p = 7
(d) p ≠ 7
Answer
B
Question. What type of straight lines will be represented by the system of equations 2x + 3y = 5 and 4x + 6y = 7?
(a) Intersecting
(b) Parallel
(c) Conincident
(d) None of these
Answer
B
Question. The vertices of the triangle formed by the lines, 5x – y = 5, x + 2y = 1 and 6x + y = 17 are
(a) (1, 0), (3, –1), (2, 5)
(b) (2, 3), (5, 6), (3, –1)
(c) (1, 2), (2, 5), (3, 6)
(d) None of these
Answer
A
Question. The value of k for which the system of linear equations 3x + y = 1, (2k –1)x + (k –1)y = 2k + 1 have no solution is
(a) k = 2
(b) k = 4
(c) k = 6
(d) k = 8
Answer
A
Question. The value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent is
(a) −14/ 3
(b) 2/ 5
(c) 5
(d) 10
Answer
D
Question. If a pair of linear equations is consistent, then the line represented by them are
(a) parallel
(b) intersecting or coincident
(c) always coincident
(d) always intersecting
Answer
B
Question. The system of simultaneous equations 3m+ n =1 and (2k -1) m+ (k -1)n = 2k +1 , is inconsistent. What is the value of ‘k’?
(a) 3
(b) 1
(c) 2
(d) 0
Answer
C
Question. The course of an enemy submarine as plotted on a set of rectangular axes gives the equation 2x + 3y = 5. On the same axes. the course of a destroyer is indicated by the equation x + y = 10 . Find the point (x, y) at which the submarine can be destroyed.
(a) (-7, 3)
(b) (7, -3)
(c) (-3, 7)
(d) (3, -7)
Answer
B
Question. Which of the following solutions do the system of equations 2x + y = 5 and x + 2y = 4 have?
(a) Consistent and a unique solution
(b) Consistent and infinitely many solutions
(c) Inconsistent
(d) No solution
Answer
A
Question. Choose the dependent system from the following.
(a) m+ n = 7, 3m+3n = 21
(b) 3x – 2y = 5 , 2x – 3y = 7
(c) 3x – 3y =18 , x – y =10
(d) 2x + y = 6 , 4x – 2y = 4
Answer
A
Question. The sum of a two-digit number and the number obtained by reversing its digits is 154. If the digits differ by 4, find the number.
(a) 95
(b) 73
(c) 84
(d) 62
Answer
A
Question. If x + 1/y = 5 and 2x + 3/y = 13 , what is the value of (2x – 3y) ?
(a) 1
(b) 2
(c) 3
(d) 5
Answer
D
Question. Rajesh buys 7 books and 6 pens for `3800 and Amar buys 3 books and 5 pens of the same kind for ₹ 1750. What are the respective costs of a book and a pen?
(a) ₹ 350, ₹ 50
(b) ₹ 500, ₹ 75
(c) ₹ 250, ₹ 100
(d) ₹ 500, ₹ 50
Answer
D
Question. The angles A, B, C and D in order in a cyclic quadrilateral are (2x + y)o ,(2(x + y))o , (3x + 2y )o , and (4x + 2y )o . Find their measures in the same order.
(a) 70°, 110°, 80°, 100°
(b) 70°, 80°, 110°, 100°
(c) 70°, 80°, 100°, 110°
(d) 80° , 100° , 110° , 70°
Answer
B
Question. What type of a system of equations is the pair of linear equations 2x – 3y = 8 and 4x – 6y = 9?
(a) Consistent system
(b) Inconsistent system
(c) Dependent system
(d) Independent system
Answer
B
Question. Find the values of ‘x’ and y, for the equations a2/x – b2/y = 0 , a2b/x + b2a/y = a + b where x, y ≠ 0 .
(a) x = a2 , y = b2
(b) x = b2 , x = a2
(c) x = b/a , y = a/b
(d) x = 1/b , y = 1/a
Answer
A
Question. The value of m and n so that the pair of linear equations (2m – 1)x + 3y = 5; 3x + (n – 1)y = 2 has infinite number of solutions respectively are
(a) 15/ 4 , 13/ 8
(b) 17, 4 , 11/ 5
(c) 11/ 8, 11/ 9
(d) None of these
Answer
B
Question. In the following questions, a statement of assertion (A) is followed by a statement reason (R). Choose the correct choice as:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
1. Assertion (A): Pair of linear equations x + y = 14, x – y = 4 is consistent.
Reason (R): By comparing a1/ a2 and b1/ b2 if we get a1/a2 ≠ b1/ b2 , then given system of equations is consistent.
2. Assertion (A): For k = 6, the system of linear equations x + 2y + 3 = 0 and 3x + ky + 6 = 0 is inconsistent.
Reason (R): The system of linear equations a1 x + b1 y + c1 = 0 and a2 x + b2 y + c2 = 0 is inconsistent if a1/ a2 = b1/ b2 = c1/ c2
Answer
1. (A) ,2. (C)
Question. The value of x and y for the following system of equations, respectively are
21/x + 47/y = 110
47/x + 21/y = 162 ⇒ x, y ≠ 0
(a) x = 1 2 , y = –1
(b) x = 1 3 , y = 1
(c) x = 1 4 , y = 2
(d) x = 1 3 , y = 1 4
Answer
B
Question. If x + 2y – 3 = 0, 3x – 2y + 7 = 0, then
(a) x = –1, y = 2
(b) x = 1, y = 2
(c) x = 2, y = 3
(d) x = – 2, y = – 3
Answer
A
Question. If 2x + y = 23 and 4x – y = 19, then the value of (5y – 2x) and (y/x – 2) respectively are
(a) 31, −5/ 7
(b) 28, 3 /11
(c) 24, 5/ 8
(d) 10, 17/ 21
Answer
A
Question. Which of the following is not a solution of the pair of equations 3x – 2y = 4 and 6x – 4y = 8?
(a) x = 2, y = 1
(b) x = 4, y = 4
(c) x = 6, y = 7
(d) x = 5, y = 3
Answer
D
Question. If 2x + y = 35 and 3x + 2y = 65, the value of x y is
(a) 1/ 2
(b)1/ 3
(c) 1/ 4
(d) 1 / 5
Answer
D
Question. If 2x = 5y + 4, 3x – 2y + 16 = 0, then
(a) x = 2, y = –2
(b) x = 3, y = –3
(c) x = 4, y = 5
(d) x = – 8, y = – 4
Answer
D
Question. If 4/x + 3y = 8 ; 6/x − 4y = −5 , then
(a) x = 2, y = 2
(b) x = 1, y = –1
(c) x = 2, y = –2
(d) x = 3, y = – 3
Answer
A
Question. In the figure, ABCDE is a pentagon with BE Q CD and BC Q DE. BC is perpendicular to CD. AB = 5 cm, AE = 5 cm, BE = 7 cm, BC = x – y and CD = x + y. If the perimeter of ABCDE is 27 cm, the value of x and y, given x, y ≠ 0, respectively are
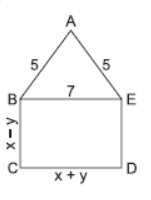
(a) x = 6, y = 1
(b) x = 3, y = 4
(c) x = 2, y = 5
(d) x = 0, y = 2
Answer
A
Question. If x/2 + y = 0.8 ; 7/x + y/2 = 10 then
(a) x = 2, y = 0.5
(b) x = 0.4, y = 0.6
(c) x = 0.3, y = 3
(d) x = 0.5, y = 0.8
Answer
B
Question. If 6(ax + by) = 3a + 2b; 6(bx – ay) = 3b – 2a, then
(a) x = 1/ 2 , y = 1/ 2
(b) x = – 1/ 2 , y = – 1/ 2
(c) x = 1/ 2 , y = 1/ 3
(d) x = – 1/ 2 , y = – 1/ 3
Answer
C
Question. If 2x + 5y – 1 = 0, 2x + 3y – 3 = 0, then
(a) x = 1, y = – 3
(b) x = 3, y = –1
(c) x = 2, y = 5
(d) x = 5, y = – 3
Answer
B
Question. If 7(y + 3) – 2(x + 2) = 14, 4(y – 2) + 3(x – 3) = 2, then
(a) x = 1, y = 4
(b) x = 3, y = 5
(c) x = 5, y = 1
(d) None of these
Answer
C
Question. Solution of the simultaneous linear equations: 2x/y − y/2 = − 1/6 and x/2 + 2y/3 = 3 is
(a) x = 2, y = – 3
(b) x = – 2, y = 3
(c) x = 2, y = 3
(d) x = – 2, y = – 3
Answer
C
Question. If 4/x + 5y = 7; 3/x + 4y = 5 , then
(a) x = 1 3 , y = –1
(b) x = 8, y = 3
(c) x = 4, y = 7
(d) x = 5, y = 9
Answer
A
Question. If 2x + 3y = 11 and 2x – 4y = –24, then the value of ‘m’ for which y = mx + 3 is
(a) 0
(b) 1
(c) –1
(d) – 2
Answer
C
Question. If 2x + 3y = 11 and x – 2y = –12, then the value of ‘m’ for which y = mx + 3 is
(a) 1
(b) –1
(c) 2
(d) – 2
Answer
B
Question. If 3 – (x – 5) = y + 2, 2(x + y) = 4 – 3y, then
(a) x = 13 /4 , y = 9/ 10
(b) x = 7/ 16 , y = 5 /8
(c) x = 4/ 9 , y = 9 /12
(d) x = 26 /3 , y = −8/ 3
Answer
D
Question. The value of x satisfying both the equations 4x – 5 = y and 2x – y = 3, when y = –1 is
(a) 1
(b) –1
(c) 2
(d) –2
Answer
A
Question. If 44/x+y + 30/x−y = 10 and 55/x+y + 40/x−y = 13 , then
(a) x = 7 , y = 7
(b) x = 2, y = 3
(c) x = 5 , y = 2
(d) x = 8, y = 3
Answer
D
Question. Aruna has only ` 1 and ` 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is ` 75, then the number of ` 1 and ` 2 coins are, respectively
(a) 35 and 15
(b) 35 and 20
(c) 15 and 35
(d) 25 and 25
Answer
D
Question. The sum of a two-digit number and the number obtained by interchanging the digits is 132. If the two digits differ by 2, the number is
(a) 45
(b) 75
(c) 85
(d) 115
Answer
B
Question. The two consecutive odd positive integers, sum of whose squares is 290 are
(a) 5, 13
(b) 11, 13
(c) 13, 17
(d) None of these
Answer
B
Question. Two years ago, a father was five times as old as his son. Two years later, his age will be 8 more than three times the age of the son. The present age of father and son, respectively are
(a) 40 years, 12 years
(b) 30 years, 6 years
(c) 32 years, 8 years
(d) 42 years, 10 years
Answer
D
Question. If 3 chairs and 1 table costs ` 1500 and 6 chairs and 1 table costs ` 2400, the pair of linear equations to represent this situation is
(a) 6x + y = 1500, 3x + y = 2400
(b) x 3 + y = 1500, x 6 + y = 2400
(c) 3x + y = 1500, 6x + y = 2400
(d) None of these
Answer
C
Question. A boat travels for 7 hours. If it travels 4 hours downstream and 3 hours upstream, then it covers the distance of 116 km. But if it travels 3 hours downstream and 4 hours upstream, it covers the distance of 108 km. The speed of the boat is
(a) 16 km/h
(b) 22 km/h
(c) 18 km/h
(d) None of these
Answer
A
Question. If 1/2x − 1/y = –1 and 1/x +1/ 2y = 8, (x ≠ 0, y ≠ 0), then
(a) x = 1/ 4 , y = 1/ 2
(b) x = 1/ 3 , y = 1/ 5
(c) x = 1/ 6 , y = 1/ 8
(d) x = 1/ 6 , y = 1/ 4
Answer
D
Question. If 2/x + 2y = 15 and 2/x − 4y = 3, then the values of x and y, respectively are
(a) 2/ 11 , 2
(b) 3, 1/ 3
(c) 4, 1/ 4
(d) 1/ 4 , 4
Answer
A
Question. The difference between two numbers is 26 and the larger number exceeds thrice of the smaller number by 4. The numbers are
(a) 39, 13
(b) 12, 38
(c) 37, 11
(d) None of these
Answer
C
Question. 1/ 3x + y + 1/ 3x – y = 3/ 4 and 1/ 2(3x +y) −1/2(3x − y) = −1/ 8 , where 3x + y ≠ 0, 3x – y ≠ 0, then
(a) 1, 2
(b) 1, 1
(c) 1, 3
(d) 1, 4
Answer
B
Question. When the following pair of equations is solved by reducing them to a pair of linear equations, we get 1/x − 4 /y = 2 and 1/x + 3/ y = 9
(a) x = 1/ 6 , y = 1
(b) x = 1, y = 1/ 5
(c) x = 1/ 3 , y = 5
(d) x = 1/ 4 , y = 1/ 3
Answer
A
Question. If 2/x + 3/y = 13 and 5/x − 4/y = –2, then x + y equals
(a) 1/ 6
(b) −1/ 6
(c) 5/ 6
(d) −5/ 6
Answer
C
Question. A purse contains 25 paise and 10 paise coins. The total amount in the purse is ` 8.25. If the number of 25 paise coins is one-third of the number of 10 paise coins in the purse, then the total number of coins in the purse is
(a) 60
(b) 40
(c) 80
(d) 72
Answer
A
Question. The vertices of the triangle formed by the graphs of the equations 4x – 3y – 6 = 0, x + 3y – 9 and y-axis are
(a) (1, 3), (2, 4), (–3, 5)
(b) (0, 3), (3, 2), (0, –2)
(c) (0, 4), (3, 3), (2, 6)
(d) None of these
Answer
B
Question. The nature of the system of equations 2x – 2y – 2 = 0 and 4x – 4y – 5 = 0 is
(a) Unique
(b) Consistent
(c) Inconsistent
(d) None of these
Answer
C
Question. Given: 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz. The pair of linear equations representing the above situation and their solution, respectively are
(a) x + y = 10, x – y = –4; (3, 7)
(b) x – y = 10, x + y = 4; (3, 5)
(c) 2x + y = 10, 2x – y = 4; (2, 5)
(d) 2x – y = 10, 2x + y = 4
Answer
A
Question. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. The dimensions of the garden are (use graphical method)
(a) Length = 20 m, width = 16 m
(b) Length = 16 m, width = 24 m
(c) Length = 18 m, width = 12 m
(d) Length = 24 m, width = 15 m
Answer
A
Question. The solution of the following system of equations when solved graphically is:
2x – 3y – 6 = 0 2x + y + 10 = 0
(a) (3, 4)
(b) (–3, –4)
(c) (4, 5)
(d) (–4, –5)
Answer
B
Question. On comparing a1/ a2 , b1/ b2 , c1/ c2 , the graphical representation of equations 2x – 3y = 8 and 4x – 6y – 9 = 0 will
(a) Intersecting lines
(b) Coincident lines
(c) Parallel lines
(d) None of these
Answer
C
Question. The coordinates of vertices of a triangle formed by the equations x – y + 1 = 0, 3x + 2y – 12 = 0 and x-axis are
(a) (1, 3), (–2, 3), (3, 0)
(b) (3, 4), (–3, 5), (2, 3)
(c) (2, 5), (–3, 0), (5, 0)
(d) (2, 3), (–1, 0), (4,0)
Answer
D
Question. Given: 5 pencils and 7 pens together cost ` 50, whereas 7 pencils and 5 pens together cost ` 46. The pair of linear equations representing the above situation and the cost of one pencil and that of one pen, respectively are
(a) 5x – 7y = 50, 7x – 5y = 46; (3, 5)
(b) 5x + 7y = 50, 7x + 5y = 46; (3, 5)
(c) 3x – 8y = 48, 3x + 8y = 48; (5, 3)
(d) None of these
Answer
B
Question. The coordinates of the vertices of a triangle formed by the equations of sides are: y = x; y = 2x; x + y = 6 are
(a) (0, 0), (3, 3), (2, 4)
(b) (0, 1), (5, 5), (2, 5)
(c) (4, 4), (3, 0), (1, 6)
(d) None of these
Answer
A
Question. On comparing a1/a2 , b1/b2 , c1/ c2 , the graphical representation of equations 3x + 2y = 5, 2x – 3y = 7 will be
(a) Intersecting
(b) Coincident
(c) Parallel
(d) None of these
Answer
A
Question. The nature of graphs of equations x + 4y = 3, 2x + 8y = 6 and the number of their solutions are
(a) Consistent, one
(b) Consistent, two
(c) Dependent, many
(d) Inconsistent, no solution
Answer
C
Question. The number of solutions of the following pair of linear equations is
x + 2y – 8 = 0
2x + 4y = 16
(a) No solutions
(b) One solution
(c) Two solutions
(d) Infinitely many solutions
Answer
D
Question. The area of the quadrilateral formed by the lines x = 3, x = 6, 2x – y – 4 = 0 and x-axis is
(a) 8 sq. units
(b) 12 sq. units
(c) 15 sq. units
(d) None of these
Answer
C
Question. The lines represented by the equations 9x + 3y + 12 = 0 and 18x + 6y + 24 will
(a) intersect at a point
(b) be parallel
(c) be coincident
(d) None of these
Answer
C
Question. The lines represented by the equations 6x – 3y + 10 = 0 and 2x – y + 9 = 0 will
(a) intersect at a point
(b) be parallel
(c) be coincident
(d) None of these
Answer
B
Question. The value of k so that the following system of equations has no solution is
3x – y – 5 = 0, 6x – 2y + k = 0
(a) 10
(b) –10
(c) Both 10 and –10
(d) All real values of k except –10
Answer
D
Question. If the pair of equations x + y = 5 and 2x + 2y = 10 is consistent, the two solutions obtained graphically are
(a) (0, 4), (4, 0)
(b) (7, –2), (2, 7)
(c) (0, 5), (5, 0)
(d) None of these
Answer
C
Question. The lines represented by the equations 5x – 4y + 8 = 0, 7x + 6y – 9 will
(a) intersect at a point
(b) be parallel
(c) be coincident
(d) None of these
Answer
A
Question. If the pair of equations x sin θ + y cos θ = 1 and x + y = √2 has infinitely many solutions, then the value of θ is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer
B
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
Question. Assertion : x + y – 4 = 0 and 2x + ky – 3 = 0 has no solution if k = 2
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are consistent if a1/a2 ≠ b1/b2
Answer
B
Question. Assertion : If the system of equations 2x + 3y = 7 and 2ax + (a + b) y = 28 has infinitely many solutions, then 2a – b = 0
Reason : The system of equations 3x – 5y = 9 and 6x – 10y = 8 has a unique solution.
Answer
C
Question. Assertion : If the pair of lines are coincident, then we say that pair of lines is consistent and it has a unique solution.
Reason : If the pair of lines are parallel, then the pair has no solution and is called inconsistent pair of equations.
Answer
D
Question. Assertion : 3x + 4y + 5 = 0 and 6x + ky + 9 = 0 represent parallel lines if k = 8
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 represent parallel lines if a1/a2 = b1/b2 ≠ c1/c2
Answer
A
Question. Assertion : If kx – y – 2 = 0 and 6x – 2y – 3 = 0 are inconsistent, then k = 3
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are inconsistent if a1/a2 = b1/b2 ≠ c1/c2
Answer
A
Question. Assertion : The linear equations x – 2y – 3 = 0 and 3x + 4y – 20 = 0 have exactly one solution
Reason : The linear equations 2x + 3y – 9 = 0 and 4x + 6y – 18 = 0 have a unique solution
Answer
C
Question. Assertion : 3x – 4y = 7 and 6x – 8y = k have infinite number of solution if k = 14
Reason : a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 have a unique solution if a1/a2 ≠ b1/b2
Answer
B



