Please refer to Continuity and Differentiability MCQ Questions Class 12 Mathematics below. These MCQ questions for Class 12 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Continuity and Differentiability will help you to prepare for the exams and get more marks.
Continuity and Differentiability MCQ Questions Class 12 Mathematics
Please see solved MCQ Questions for Continuity and Differentiability in Class 12 Mathematics. All questions and answers have been prepared by expert faculty of standard 12 based on the latest examination guidelines.
MCQ Questions Class 12 Mathematics Continuity and Differentiability
Question. f (x) = 1/1+tan x
(a) is a continuous, real-valued function for all x ∈ (– ∞, ∞)
(b) is discontinuous only at x = 3π/4
(c) has only finitely many discontinuities on (– ∞, ∞)
(d) has infinitely many discontinuities on (– ∞, ∞)
Answer
D
Question. If f(9)=9,f'(9)=4,then
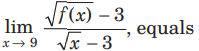
(a) 2
(b) 4
(c) 6
(d) 0
Answer
B
Question.
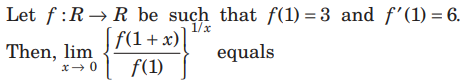
(a) 1
(b) e 1/2
(c) e2
(d) e3
Answer
C
Question.

where {x}denotes the fractional part of x,is equal to
(a) –1
(b) 0
(c) 1
(d) does not exist
Answer
D
Question. If f (x+Y/3) = 2+f(x) f(y)/3 for all real x and y and f′(2)=2,
(a) 2x+1
(b) 2x
(c) 2x+2
(d) Constant
Answer
C
Question. Let f Q :[1 ,10] → Q be a continuous function and f(1) = 10, then f(10) is equal to
(a) 1/10
(b) 10
(c) 1
(d) Cannot be obtained
Answer
B
Question. If (x + y)= f(x) f(y) for all x ,y ∈ R, f(5)=2 and (0) =3. Then, f ′(5) equals
(a) 6
(b) 5
(c) 4
(d) 3
Answer
A
Question.

(a) 1/24
(b) 1/5
(c) − √24
(d) 1/2√6
Answer
D
Question.
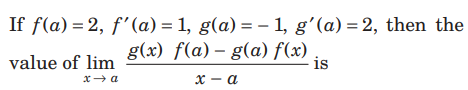
(a) –5
(b) 1/5
(c) 5
(d) 1
Answer
C
Question. ABC is an isosceles triangle inscribed in a circle of radius r. If AB AC = and h is the altitude from
(a) 1/r
(b) 1/64r
(c) 1/128r
(d) 1/2r
Answer
C
Question.
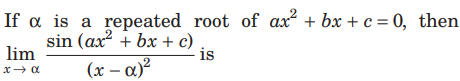
(a) 0
(b) a
(c) b
(d) c
Answer
B
Question. If f is strictly increasing function, then lim f(x2)-f(x)/f(x)-f(0) is equal to
x→0
(a) 0
(b) 1
(c) −1
(d) 2
Answer
C
Question.
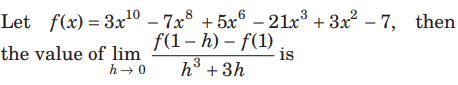
(a) 53/3
(b) 22/3
(c) 13
(d) 22 13
Answer
A
Question.
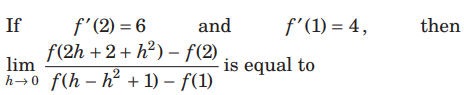
(a) does not exist
(b) –3/2
(c) 3/2
(d) 3
Answer
D
Question.
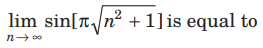
(a) ∞
(b) 0
(c) does not exist
(d) None of these
Answer
B
Question.
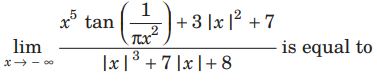
(a) − 1/ π
(b) 0
(c) ∞
(d) does not exist
Answer
A
Question. The function defined by
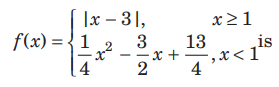
(a) continuous at x = 1
(b) continuous at x = 3
(c) differentiable at x = 1
(d) All of the above
Answer
C
Question.

(a) 0
(b) f(x)
(c) g(x)
(d) None of the above
Answer
B
Question.
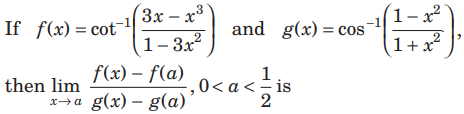
(a) 3/2(1+a2)
(b) 3/2(1+x2)
(c) 3/2
(d) −3/2
Answer
D
Question.

(a) f(x) is differentiable at x = 0
(b) f(x) is continuous at x = 0 1,
(c) f(x) is differentiable at x = 1
(d) None of the above
Answer
B
Question. lim |x| , [cos x] ,where [.] is the greatest integer
x →o
function, is
(a) 1
(b) does not exist
(c) 0
(d) None of these
Answer
A
Question. If , y = e3x+7 , then the value of dy/dx|x=0 is
(a) 1
(b) 0
(c) – 1
(d) 3e7
Answer
D
Question. If y = sec x°, then dy/dx is equal to :
(a) sec x tan x
(b) sec x° tan x°
(c) π/180 sec x° tan x°
(d) None of these
Answer
C
Question. Let f(x) = sinx, g(x) = x2 and h(x) = logex.
If F(x) = (hogof) (x), then F'(x) is equal to
(a) a cosec3x
(b) 2 cot x2 – 4x2 cosec2x2
(c) 2x cot x2
(d) – 2 cosec2x
Answer
D
Question. All the points of discontinuity of the function f defined by
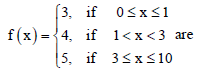
(a) 1,3
(b) 3,10
(c) 1,3,10
(d) 0,1,3
Answer
A
Question.
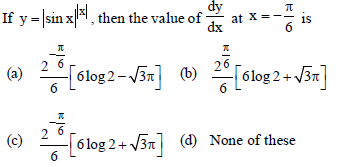
Answer
A
Question.
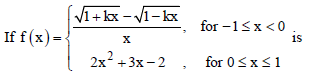
is continuous at x = 0, then k is equal to
(a) – 4
(b) – 3
(c) – 2
(d) – 1
Answer
C
Question. The value of the derivative of |x – 1| + |x – 3| at x = 2 is :
(a) –2
(b) 0
(c) 2
(d) not defined
Answer
B
Question. If f (x) = (x + 1)cot x be continuous at x = 0 then f (0) is equal to:
(a) 0
(b) – e
(c) e
(d) None
Answer
C
Question.

(a) 1/2
(b) 1/4
(c) 2
(d) 3/2
Answer
B
Question.
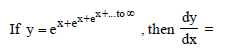
(a) y2/1– y
(b) y2/y –1
(c) y/1– y
(d) –y/1– y
Answer
C
Question.
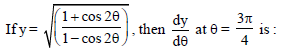
(a) – 2
(b) 2
(c) ± 2
(d) None of these
Answer
A
Question.
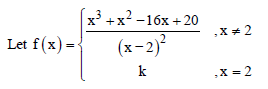
If f(x) is continuous for all x, then k =
(a) 3
(b) 5
(c) 7
(d) 9
Answer
C
Question.
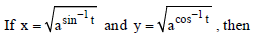
(a) x dy/dx + y = 0
(b) x dy/dx = y
(c) y dy/dx = x
(d) None of these
Answer
A
Question.

is continuous at x = 0, then the value of k is
(a) 1
(b) – 2
(c) 2
(d) 1/2
Answer
C
Question. The number of discontinuous functions y(x) on [– 2, 2] satisfying x2 + y2 = 4 is
(a) 0
(b) 1
(c) 2
(d) > 2
Answer
A
Question.
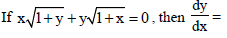
(a) x + 1/x
(b) 1/1+ x
(c) – 1/(1 + x)2
(d) x/1+ x
Answer
C
Question. A value of c for which the Mean Value Theorem holds for the function f(x) = logex on the interval [1, 3] is
(a) 2 log3e
(b) 1/2log3e
(c) log3e
(d) loge3
Answer
A
Question. If the function,

is continuous in the interval [0,π] then the value of (a, b) are :
(a) (– 1, – 1)
(b) (0, 0)
(c) (– 1, 1)
(d) (1, 0)
Answer
B
Question. If y = logax + logxa + logxx + logaa, then dy/dx is equal to
(a) 1/x + x log a
(b) log a/x + x/log a
(c) 1/x log a + x log a
(d) 1/x log a – log a/x (log x)2
Answer
D
Question. If x = 1–t2/1+t2 and 2t/1+t2 , then dy/dx is equal to :
(a) – y/x
(b) y/x
(c) – x/y
(d) x/y
Answer
C
Question. If y = log tan √x then the value of dy/dx is :
(a) 1/2√x
(b) sec2√x/√x tan x
(c) 2sec2√x
(d) sec2√x/2√xtan√x
Answer
D
Question.

is continuous at x = 2 and 4, then the values of a and b are.
(a) a = 3, b = –5
(b) a = –5, b = 3
(c) a = –3, b = 5
(d) a = 5, b = –3
Answer
A
Question.
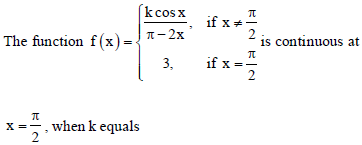
(a) – 6
(b) 6
(c) 5
(d) – 5
Answer
B
Question. Let f (x) be a twice differentiable function and f ” (0) = 5, then the value
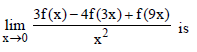
(a) 0
(b) 120
(c) –120
(d) does not exist
Answer
B
Question. Suppose f is a real function and c is a point in its domain. The derivative of f at c is defined by (if limit exist)

Answer
B
Question.
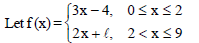
If f is continuous at x = 2, then what is the value of l ?
(a) 0
(b) 2
(c) – 2
(d) – 1
Answer
C
Question. In the interval [7, 9] the function f(x) = [x] is discontinuous at _______, where [x] denotes the greatest integer function
(a) 2
(b) 4
(c) 6
(d) 8
Answer
D
Question. If 2f (sin x) + f (cos x) = x , then d/dx f (x) is
(a) sin x + cos x
(b) 2
(c) 1/√1 – x2
(d) None of these
Answer
C
Question. The number of points at which the function f(x) = 1/x-[x], [.] denotes the greatest integer function is not continuous is
(a) 1
(b) 2
(c) 3
(d) None of these
Answer
D
Question. The function f(x) = cot x is discontinuous on the set
(a) {x = nπ,n ∈ Z}
(b) {x = 2nπ,n ∈ Z}
(c) {x = (2n+1)π/2 ;n ∈ Z}
(d) {x = nπ/2,n ∈ Z}
Answer
D
Question. If y = (tanx)sin x, then dy/dx is equal to
(a) sec x + cos x
(b) sec x + log tan x
(c) (tan x)sin x
(d) None of these
Answer
D
Question. If y = (cos x2)2, then dy/dx is equal to :
(a) – 4x sin 2x2
(b) – x sin x2
(c) – 2x sin 2x2
(d) – x cos 2x2
Answer
C
Question.
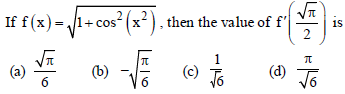
Answer
B
Question. The point of discontinuity of f (x) = tan (πx/x+1) other than x = –1 are :
(a) x = 0
(b) x = π
(c) x = 2m+1/1– 2m
(d) x = 2m–1/2m+1
Answer
C
Question. If f(x) = (logcot xtan x)(logtanxcot x)–1 + tan–14x/4–x2 , then f'(2) is equal to
(a) 1/2
(b) –1/2
(c) 1
(d) – 1
Answer
A
ASSERTION – REASON TYPE QUESTIONS
(a) Assertion is correct, reason is correct; reason is a correct explanation for assertion.
(b) Assertion is correct, reason is correct; reason is not a correct explanation for assertion
(c) Assertion is correct, reason is incorrect
(d) Assertion is incorrect, reason is correct.
Question. Assertion : If y = log10x + logey, then
dy/dx = log10e/x (y/y–1)
Reason : d/dx(log10x) = log x/log10
and d/dx (logex) = log x/loge
Answer
C
Question. Assertion : f (x) = xn sin(1/x) is differentiable for all real values of x (n ≥ 2).
Reason : For n ≥ 2,limx→0 f(x) = 0
Answer
D
Question. Consider the function
f(x) = [sin x], x ∈ [0, π]
Assertion: f(x) is not continuous at x = π/2
Reason : lim f(x)x→π/2 does not exist
Answer
C
Question. Assertion : The function f(x) = |x|/x is continuous at x = 0.
Reason : The left hand limit and right hand limit of the function f(x) = |x|/x = are not equal at x = 0.
Answer
D
Question. Assertion : If a function f is discontinuous at c, then c is called a point of discontinuity.
Reason : A function is continuous at x = c, if the function is defined at x = c and the value of the function at x = c equals the limit of the function at x = c.
Answer
B
Question. Assertion : d/dx ecos x = ecos x (– sin x)
Reason : d/dx ex = ex
Answer
B
Question.
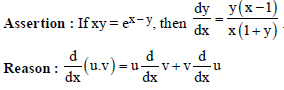
Answer
B
Question. Assertion : For x < 0, d/dx(ln|x|) = –1/x
Reason : For x < 0, |x| = – x
Answer
D


