Please refer to Triangles MCQ Questions Class 10 Mathematics below. These MCQ questions for Class 10 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Triangles will help you to prepare for the exams and get more marks.
Triangles MCQ Questions Class 10 Mathematics
Please see solved MCQ Questions for Triangles in Class 10 Mathematics. All questions and answers have been prepared by expert faculty of standard 10 based on the latest examination guidelines.
MCQ Questions Class 10 Mathematics Triangles
Question. In the follwoing figure AD : DB = 1 : 3, AE : EC = 1 : 3 and BF : FC = 1 : 4, then
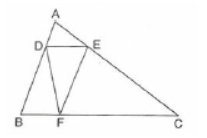
(a) AD ll FC
(b) AD ll FE
(c) DE ll BC
(d) AE ll DF
Answer
C
Question. If in two triangles ABC and PQR, ∠A= ∠Q and ∠R=∠B , andthen which of the following is not true.
(a) AB/PQ =BC/RP
(b) BC/PR =AC/PQ
(c) BC/RP =AB/QR
(d) AB/QR =AC/PQ
Answer
A
Question. In the given figure if BP ll CF ,DP ll EF , then AD: DE is equal to

(a) 1 : 3.
(b) 3 : 4.
(c) 2 : 3.
(d) 1 : 4.
Answer
A
Question. In the given figure PQ ll B(c) AP/PB =4, then the value of AQ/AC is

(a) 5
(b) 4/5
(c) 4
(d) 5/4
Answer
B
Question. If ΔABC∼PQR such that AB = 9.1 cm and PQ = 6.5 cm. If the perimeter of ΔPQR is 25 cm, then the perimeter of ΔABC is
(a) 34 cm
(b) 35 cm
(c) 36 cm
(d) 30 cm
Answer
B
Question. Out of the given statements
i. The areas of two similar triangles are in the ratio of the corresponding altitudes.
ii. If the areas of two similar triangles are equal, then the triangles are congruent.
iii. The ratio of areas of two similar triangles is equal to the ratio of their corresponding medians.
iv. The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides.
The correct statement is
(a) (iii)
(b) (ii)
(c) (i)
(d) (iv)
Answer
B
Question. If ΔABC is an equilateral triangle of side ‘a’ and D is a point on BC such that BD = – BC, what is the length of AD?
(a) √7/3 a
(b) 3/√7 a2
(c) √7/3 a
(d) √7/3 a2
Answer
C
Question. Given that PB ⊥ AB and QA ⊥ AB PO=4 cm and QO = 7cm , if area of ΔQAO is 245 cm2 , what is the area of ΔPBO?
(a) 2 60 cm
(b) 2 40 cm
(c) 2 125cm
(d) 2 80cm
Answer
D
Question. In ∠ABC , if AD/DB = AE/EC and ∠ADE = ∠ACB , what type of triangle is ΔABC ?
(a) Right triangle
(b) Acute angled triangle
(c) Isosceles triangle
(d) Obtuse angled triangle
Answer
C
Question. In the given figure, AD -L BC, BC = a, CA = b, and AB = c.
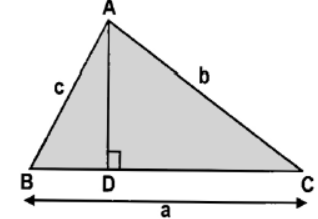
If BD = 1/3 CD , what is the value of 2b2 ?
(a) a2 – 2c2
(b) 2a2 + c2
(c) c2 – 2a2
(d) 2a2 + 2c2
Answer
D
Question. Two 15 m strings are tied to a peg between two poles 9 m and 12 m long from their types. What is the distance between the poles?
(a) 18m
(b) 21 m
(c) 20 m
(d) 23 m
Answer
B
Question. In ΔABC,∠A = 90° and AD±BC. If AB= 5 cm, BC = a cm and AC = b cm, find the length of BD in cm.
(a) (b2 – a2 + 25/ a)
(b) (a2 – b2 + 25/ 2a)
(c) (a2 + b2 + 25/ 2b)
(d) (a2 – b2 + 25/ 2a)
Answer
B
Question. In the given figure what is the value of ‘ x ‘ if AB||CD ?
(a) 2 units
(b) 4 units
(c) 3 units
(d) 5 units
Answer
C
Question. X and Y are points on the sides AB and AC respectively of ΔABC.
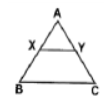
If AB = 5.6 cm, AX = 1.4 cm, AC = 7.2 cm, and XY||BC , what is the measure of AY?
(a) 2.4 cm
(b) 1.6cm
(c) 1.8 cm
(d) 3.6cm
Answer
C
Question. In ΔABC, ∠B> 90° and AD ⊥ CB (produced). Identify the correct statement.
(a) AC2 = AB2 + BC2 + 2BC.AD
(b) AC2 = AB2 + BC2 + 2BC.AB
(c) AB2 = AC2 + BC2 + 2BC.BD
Answer
A
Question. If ΔABC ∼ ΔDFE ∠A =30° , ∠C = 50° , AB = 5cm, ∠AC = 8cm and DF = 7.5 cm . Which of the following is true ?
(a) DE = 12cm, ∠F = 50°
(b) DE = 12cm, ∠F =100°
(c) EF = 12cm, ∠D =100°
(d) EF = 12cm, ∠D = 30°
Answer
B
Question. If in two triangles ABC and DEF, AB/DE =BC/FE =CA/FD , then
(a) ΔFDE ∼ ΔABC
(b) ΔBCA ∼ ΔFDE
(c) ΔFDE ∼ ΔCAB
(d) ΔCBA ∼ ΔFDE
Answer
C
Question. In the adjoining figure P and Q are points on the sides AB and AC respectively of ΔABC such that AP = 3.5 cm, PB = 7cm, AQ = 3cm, QC = 6cm and PQ = 4.5cm. The measure of BC is equal to
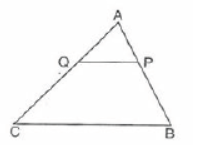
(a) 9 cm
(b) 15 cm
(c) 12.5 cm
(d) 13.5 cm
Answer
D
Question. In the given figure if ΔAED ∼ ΔABC , then DE is equal to

(a) 6.5 cm
(b) 5.6 cm
(c) 5.5 cm
(d) 7.5 cm
Answer
B
Question. A semicircle is drawn on A(c) Two chords AB and BC of length 8 cm and 6 cm respectively are drawn in the semicircle. What is the measure of the diameter of the circle?
(a) 10 cm
(b) 12 cm
(c) 11 cm
(d) 14 cm
Answer
A
Question. In the given figure, if ar(ΔALM)/ar(trapezium LMCB) =9/16 , Then AL: LB is equal to
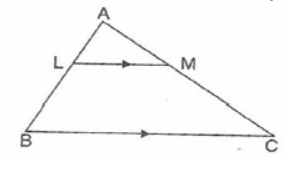
(a) it is 3 : 5
(b) it is 3 : 4
(c) it is 3 : 2
(d) it is 2 : 3
Answer
C
Question. In an isosceles triangle ABC if AC = BC and AB2 = 2AC2 then the measure of ∠C is
(a) 90o
(b) 45o
(c) 60o
(d) 300
Answer
A
Question. In the given figure XY || B(c) If AX = 3cm, XB = 1.5cm and BC = 6cm, then XY is equal to
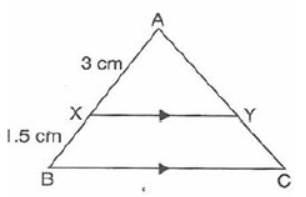
(a) 6 cm.
(b) 4.5 cm
(c) 3 cm.
(d) 4 cm.
Answer
D
Question. What will be the length of the hypotenuse of an isosceles right triangle whose one side is 4√2cm
(a) 12√2cm
(b) 12 cm.
(c) 8 cm.
(d) 8√2
Answer
C
Question. In the given figure if ∠ADE = ∠ABC , then CE is equal to
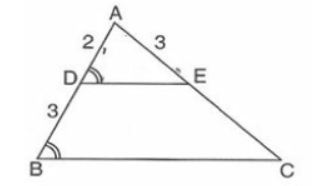
(a) 2.
(b) 4.5.
(c) 5.
(d) 3.
Answer
B
Question. In the given figure, if ar (ΔALM)/ar(traperium LMCB)=9/16, and LM||BC, Then AL:LB is equal to
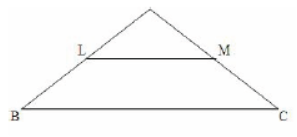
(a) 3 : 5
(b) 4 : 1
(c) 3 : 4
(d) 2 : 3
Answer
B
Question. In the given figure, the value of x is:-

(a) 15 cm
(b) 10 cm
(c) 12 cm
(d) 6 cm
Answer
B
Question. In the adjoining figure AC || B(d) If , EB = 4 cm, ED = 8 cm, AC = 6 cm, AE = 3 cm then CE and BD are respectively
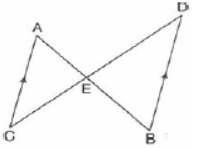
(a) 5 cm, 7 cm.
(b) 7.5 cm, 9.5 cm.
(c) 6 cm, 8 cm.
(d) 4 cm, 6 cm.
Answer
C
Question. A street light is fixed on a pole 6 m above the groun(d) If a woman of height 1.5 m casts a shadow of 3, then distance between her and the base of the pole is _____.
(a) 12 m
(b) 9 m
(c) 8 m
(d) 10 m
Answer
B
Question. In an equilateral ΔABC AD⊥ BC and AD2 =P. BC2 , then p is equal to
(a) 1/2
(b) 3/4
(c) 2/3
(d) 1/3
Answer
B
Question. ABCD is a trapezium in which AB || DC and AB = 2D(c) Diagonals AC and BD intersect at O. If ar(ΔAO) = 84 cm2, ar (ΔCOD) then is equal to
(a) 24 cm2
(b) 42 cm2
(c) 28 cm2
(d) 21 cm2
Answer
D
Question. It is given that ΔABC ∼ ΔDFE , ∠A = 30° , ∠C =40°, AB =5 cm, AC =8cm and DF =7.5 cm Then, the following is true.
(a) ∠F =100° ,DE =12cm
(b) ∠F =40° ,DE =12cm
(c) ∠D =110° ,EF =12cm
(d) ∠D =30° , EF =12cm
Answer
A
Question. The areas of two similar triangles are respectively . If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is equal to
(a) 8.1 cm
(b) 8.8 cm
(c) 11 cm
(d) 11.1 cm
Answer
B
Question. In an equilateral triangle ABC, D is a point on the side BC such that BD = 1 3 BC. Then 9AD2 =
(a) 7 AB2
(b) 5 AB2
(c) 8 AB2
(d) 11 AB2
Answer
A
Question. If in the given figure, AB ll DE and BD ll EF, then DC2 =
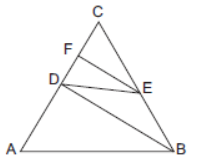
(a) CF + AC
(b) CF × AC
(c) CF + 2AC
(d) None of these
Answer
B
Question. A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s. If the lamp is 3.6 m above the ground, the length of her shadow after 4 seconds is
(a) 1.1 cm
(b) 1.6 cm
(c) 2.3 cm
(d) 3.5 cm
Answer
B
Question. Two poles of height a and b (b > a) are c metres apart. The height h (in metres) of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is
(a) ab
(b) ab + 2ab
(c) ab /a + b
(d) None of these
Answer
C
Question. In the given figure, MN || QR. If PM = x cm, MQ = 10 cm, PN = (x – 2) cm, NR = 6 cm, then the value of x is

(a) 5 cm
(b) 7 cm
(c) 8 cm
(d) 12 cm
Answer
A
Question. In the given figure, AP = 3 cm, AR = 4.5 cm, AQ = 6 cm, AB = 5 cm, AC = 10 cm. The length of AD is
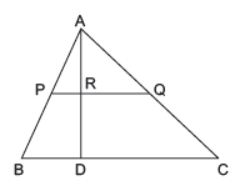
(a) 4.5 cm
(b) 6.5 cm
(c) 7 cm
(d) 7.5 cm
Answer
D
Question. AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Then area (DADE) : area (DABC) =

(a) 1 : 2
(b) 2 : 5
(c) 3 : 4
(d) 3 : 7
Answer
C
Question. In the given figure, ΔABC ∼ ΔDEF, BC = 3 cm, EF = 4 cm and area of ΔABC = 54 cm2. Then the area of ΔDEF is
(a) 54 cm2
(b) 88 cm2
(c) 96 cm2
(d) 108 cm2
Answer
C
Question. If two sides of a right triangle are 9 cm and 12 cm, then its third side will be
(a) 21 cm
(b) 15 cm
(c) 3 cm
(d) None of these
Answer
B
Question. Two poles of height 8 m and 13 m are standing 12 m apart. The distance between their tops is _____
(a) 15 m
(b) 17 m
(c) 13 m
(d) 19 m
Answer
C
(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.
Question. Assertion : ABC is an isosceles, right triangle, right angled at C. Then AB2 = 3AC2.
Reason : In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C = 90°.
Answer
D
Question. Assertion : ABC and DEF are two similar triangles such that BC = 4 cm, EF = 5 cm and area of ΔABC = 64 cm2, then area of ΔDEF = 100 cm2.
Reason : The areas of two similar triangles are in the ratio of the squares of the corresponding altitudes.
Answer
B
Question. Assertion : If in a ΔABC, a line DE || BC, intersects AB in D and AC in E, then AB /AD = AC/ AE .
Reason : If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
Answer
A
One Word Questions :
Question. Express x in the terms of a, b and c in the following figure.

Answer
ac/b + c
Question. In figure, find AD if :–
CAB ∼ ADB

Answer
1.5cm
Question. The perimetres of two similar triangles ABC and PQR are respectively 36cm and 24cm. If PQ = 10cm, find AB.
Answer
15cm
Question. The lengths of sides of a triangle are 12cm, 16cm and 21cm. The bisector of the greatest angle divides the opposite side into two parts. Find the length of these two parts.
Answer
9cm, 12cm
Question. In figure, BP ll CF , and DP ll EF , find AD/DE .

Answer
1 : 3
Question. In figures, find ∠M .
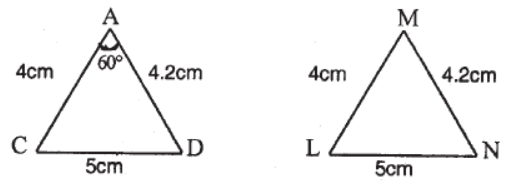
Answer
60°
Question. AB=5cm, BC=2cm and AC = √29 cm are the sides of ABC. Then what is the measure of B ?
Answer
90°
Question. ΔBAC is an isosceles Δ with AB = AC, AD is the bisector of ∠BAC . Find BD/DC .
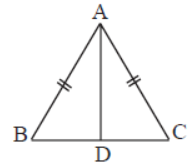
Answer
1
Question. In figure, DE ll BC and AD : DB = 2 : 3. Find ar(ΔADE) : ar(ΔABC) .

Answer
4 : 25
Question. AD is a median of a ΔABC . DE and DF are bisectors of ∠ADB and ∠ADC meeting AB and AC at E and F respectively. If AE = 3cm, BE = 4cm and AF = 15cm, find FC.
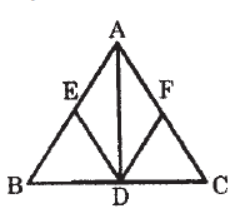
Answer
20cm
Question. In figures ΔPQR ∼ ΔXYZ , find the value of ∠Y and ∠Z .
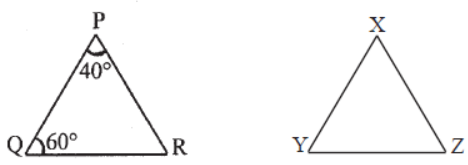
Answer
∠Y =60°, ∠Z =80°
Question. In ΔABC , PQ ll BC , find CQ.
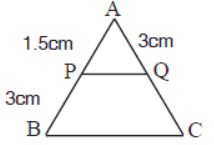
Answer
6cm
Question. In an equilateral ΔABC of side ‘a’, what is the height of ΔABC ?
Answer
√3/2 a
Question. In figure, point P divides the line segment internally. What is the ratio PA : PB?
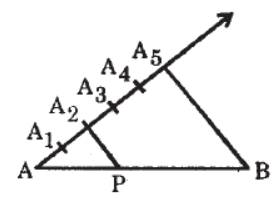
Answer
2 : 3
Question. In a triangle, the internal bisector of angle bisect the opposite side; what type of triangle is this?
Answer
Isosceles
Question. In figures, find ar (ΔPQR)/ar (ΔLMN)
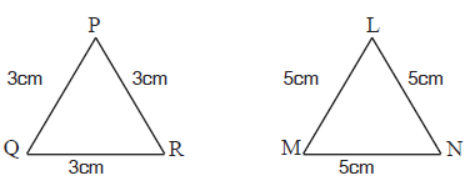
Answer
9/25
Question. A boy goes 15m due east and 20m due north. How far is he from the starting point?
Answer
25cm
Question. In figure, AD is bisector of ∠A, find AB/AC.
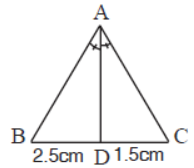
Answer
5/3
Question. In figure, PR = 6cm and AB ll QR . Find BP.
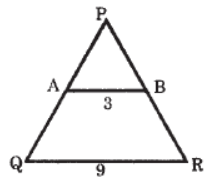
Answer
2cm
Question. If ΔABC ∼ ΔDEF , ar(ΔDEF)=100cm² and AB/DE = 1/2 . then find the area of ΔABC .
Answer
25cm²
Question. In figure, AD is the internal bisector of ∠BAC . If AB = 6cm, AC = 4cm and BD = 2.4cm, find BC.
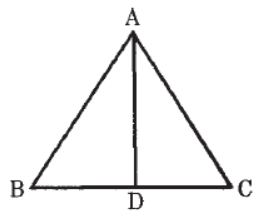
Answer
4cm
Question. In figure, ∠S =∠PRQ, MN ll QR . Write the names of similar triangles.
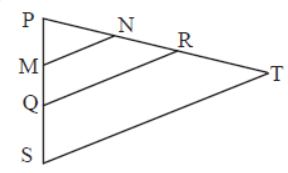
Answer
ΔPQR ∼ ΔPTS , PMN
Question. A ladder is placed in such a way that its foot is at a distance 5cm from the wall and its top reaches a window 12cm above the ground. Determine the length of the ladder.
Answer
13cm
Question. Two triangle ABC and DEF are similar. If AB = 10cm and DE = 8cm, find the ratio of the areas of ΔABC and ΔDEF .
Answer
25/16
Question. In figure, AD : DB = 1 : 3, AE : EC = 1 : 3 and BF : FC = 1 : 4, find which two lines are parallel.
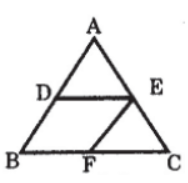
Answer
DE ll BC



