MCQ Chapter 8 Trigonometry Class 10 Mathematics

Please refer to Trigonometry MCQ Questions Class 10 Mathematics below. These MCQ questions for Class 10 Mathematics with answers have been designed as per the latest NCERT, CBSE books, and syllabus issued for the current academic year. These objective questions for Trigonometry will help you to prepare for the exams and get more marks.

Trigonometry MCQ Questions Class 10 Mathematics

Please see solved MCQ Questions for Trigonometry in Class 10 Mathematics. All questions and answers have been prepared by expert faculty of standard 10 based on the latest examination guidelines.

MCQ Questions Class 10 Mathematics Trigonometry

Question. The value of tan³θ/1+ tan²θ + cot³θ/1+ cot²θ
(a) 1−sin²θ cos²θ/2sin θ cos θ
(b) 1+2sin²θ cos²θ/sin θ cos θ
(c) 1−2sin² θ cos² θ/sin θ cos θ
(d) 2sin²θ cos²θ/1− sinθ cosθ

Question. Select the equation represented by the graph below.

(a) y = cos x
(b) y = sin x
(c) y = tan x
(d) y = − sin x

Question. If x = r cos α, cos β, y = r cosa sinb and z = r sin a then x² + y² + z² is equal to
(a) r²
(b) r⁴
(c) 1
(d) None of these

Question. Select the equation represented by the graph below.

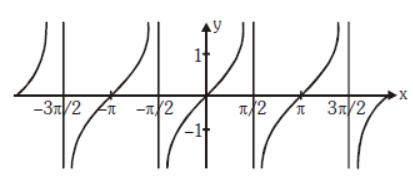
(a) y = cot x
(b) y = − cot x
(c) y = tan x
(d) y = − tan x

Question. The angle of elevation of the top of two vertical towers as seen from the middle point of the line joining the feet of the towers are 60° and 30° respectively. The ratio of heights of the towers is :-
(a) 2 : 1
(b) √3 : 1
(c) 3 : 2
(d) 3 : 1

Question. A person standing on the bank of a river observes that the angles subtended by a tree on the oppo- site bank is 60°. When he retires 40 m from the bank, he finds the angle to be 30°. The breadth of the river is
(a) 40 m
(b) 60 m
(c) 20 m
(d) 30 m

Question. A tower of height h standing at the centre of a square with sides of length a makes the same angle a at each of the four corners. Then a²/h² cot² α is :-
(a) 1
(b) 3/2
(c) 2
(d) 4

Question. If sec A + tan A = x, then sec A =
(a) x² -1/x
(b) x² – 1/2x
(c) x² + 1/x
(d) x² +1/ 2x

Question. A river flows due North, and a tower stands on its left bank. From a point A upstream and on the same bank as the tower, the elevation of the tower is 60° and from a point B just opposite A on the other bank the elevation is 45°. If the tower is 360 m high, the breadth of the river is :-
(a) 120 √6 m
(b) 240/√ 3 m
(c) 240 √3 m
(d) 240 √6 m

Question. A tower subtends an angle of 30° at a point on the same level as the foot of tower. At a second point h m high above the first, the depression of the foot of tower is 60°. The horizontal distance of the tower from the point is:-
(a) h/√3
(b) h cot60/√3 °
(c) hcot60/3 °
(d) h cot 30°

Question. The angle of elevation of a cloud at a height h above the level of water in a lake is a and the angle of depression of its image in the lake is b. The height of the cloud above the surface of the lake is equal to
(a) h(tanβ + tanα)/ (tanβ − tanα) 
(b) hcos(α+β)/ sin(β−α) 
(c) h(cotα + cotβ)/ cosα −cosβ
(d) h

Question. The value of tan 1° tan 2° tan 3° … tan 89° is
(a) 0
(b) 1
(c) − 1
(d) 2

Question. A balloon of radius r subtends an angle a at the eye of an observer and the elevation of the centre of the balloon from the eye is b, the height h of the centre of the balloon is given by :-
(a) r sinβ/ sin α
(b) r sin β sin α
(c) r sinβ/ sin( α/2)
(d) r sinα/ sin(β/2) 

Question. Select the equation represented by the graph below.

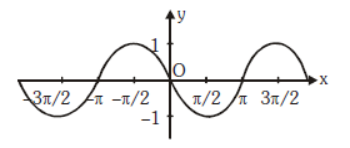
(a) y = cos x
(b) y = sin x
(c) y = tan x
(d) y = − sin x

Question. A man observes that when he moves up a distance c metres on a slope, the angle of depression of a point on the horizontal plane from the base of the slope is 30°, and when he moves up further a distance c metres, the angle of depression of that point is 45°. The angle of inclination of the slope with the horizontal is :-
(a) 60°
(b) 45°
(c) 75°
(d) 30°

Question. If x tan 45° sin 30° = cos 30° tan 30°, then x is equal to
(a) √3 
(b) 1/2
(c) 1/√2
(d) 1

Question. A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 m away from the tree, the angle of elevation becomes 30°. The breadth of the river is
(a) 40 m
(b) 20 m
(c) 30
(d) 60 m

Question. The top of a hill observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. The height of hill is :-
(a) hcotp/ cotq − cotp
(b) hcotp /cotp−cotq
(c) htanp/ tanp−tanq 
(d) htanp/ tanq − tanp 

Question. If 7 sin²θ+ 3 cos²θ = 4, then tan θ =
(a) ± 1/3
(b) ± 1/ 2
(c) ± 1 /√3
(d) ± 1 /√2

Question. A man standing on a level plane observes the elevation of the top of a pole to be a. He then walks a distance equal to double the height of the pole and finds that the elevation is now 2a. Then a =
(a) π/6
(b) π/4
(c) π/12
(d) π/8

Question. If A, B and C are interior angles of a ΔABC, then cos (B+C/2) is equal to
(a) sin A/ 2
(b) − sin A/2
(c) cos A/ 2
(d) − cos A/2

Question. If cot θ + cos θ = p and cot θ − cos θ = q, then the value of p² − q² is :
(a) 2√ pq
(b) 4 √pq
(c) 2pq
(d) 4pq

Question. Find the value of 1/(1+tan²θ) + 1/(1 +cot²θ)
(a) 1/2
(b) 2
(c) 1
(d) 1/4

Question. AB is vertical tower. The point A is on the ground and C is the middle point of AB. The part CB subtend an angle a at a point P on the ground. If AP = nAB, then tan a =
(a) n(n² + 1)
(b) n/2n²−1 
(c) n²/2n² +1 
(d) n/2n² +1 

Question. If tan q = p/q, then psinθ −qcosθ/ psinθ + qcosθ =
(a) (p² + q²)/(p² − q²)
(b) (p² − q²)/(p2 + q²)
(c) (p² + q²)/(p² − q²)
(d) None of these

Question. The angle of elevation of the top of a tower from a point A due south of the tower is a and from a point B due east of the tower is b. If AB = d, then the height of the tower is :-
(a) d/√tan² α −tan²β
(b) d/√tan² α +tan²β 
(c) d/√cot² α +cot² β
(d) d/√cot² α −cot²β

Question. If tan A + sin A = m and tan A − sin A = n, then (m² −n²)²/mn =
(a) 4
(b) 3
(c) 16
(d) 9

Question. One side of a parallelogram is 12 cm and its area is 60 cm². If the angle between the adjacent sides is 30°, then its other side is
(a) 10 cm
(b) 8 cm
(c) 6 cm
(d) 4 cm

Question. If cosec θ − sinθ = m and sec θ − cosθ = n then (m²n)^2/3 + (mn²)^2/3 =
(a) −1
(b) 1
(c) 0
(d) None of these

Question. At the foot of a mountain, the elevation of its summit is 45°. After ascending one kilometer the mountain upon and incline of 30°, the elevation changes to 60°. The height of the mountain is
(a) 1.366 km
(b) 1.266 km
(c) 1.166 km
(d) 1.466 km

Question. Which of the following statement is true:     
(a) cosec A/sin A = cos A
(b) cos A/sin A =sec A
(c) sin A/cosec A = cot A
(d) sin A/cos A = tan A 

Question. 1- tan² 45°/1 + tan² 45°   
(a) sin 45°
(b) 0
(c) cos 45°
(d) tan 45°

Question. The value of tan 15° tan 20° tan 70° tan 75°  is     
(a) 2
(b) 0
(c) 1
(d) -1

Question. If x cos A = 1 and tan A = y, then the value of x²-y²  is   
(a) -1
(b) 0
(c) 1
(d) 2

Question. If sin θ=1/2 and cosΦ=1/2, then the value of (θ +Φ ) is     
(a) 0°
(b) 30°
(c) 90°
(d) 60°

Question. The value of 2tan² 45° +cos² 30° – sin² 60° is   
(a) 0
(b) 1
(c) 2
(d) -2

Question. Choose the correct option and justify your choice:sin 2A = 2 sin A is true when A =     
(a) 45°
(b) 0°
(c) 30°
(d) 60

Question. The value of tan 30°/cot 60°  is   
(a) 1
(b) 1/√3
(c) 1/√2
(d) √2

Question. Choose the correct option and justify your choice: 1-tan² 45° /1+ tan² 45°   
(a) tan 90°
(b) 1
(c) sin 45°
(d) 0

Question. The value of cosec⁴ A-2 cosec² A+1 is   
(a) tan⁴ A
(b) sec⁴ A
(c) cosec⁴ A
(d) cot⁴ A

Question. Given that sinα =1/√2 and cos β=1/√2 , then the value of (α +β) is     
(a) 90°
(b) 45°
(c) 60°
(d) 30°

Question. cot A tan A   
(a) tan A
(b) sec A
(c) 1
(d) cot A

Question. If A and B are acute angles and sin A = cos B, then the value of (A + B) is     
(a) 0°
(b) 90°
(c) 30°
(d) 60°

Question. If sinθ =5/13  then cosθ =   
(a) 13/12
(b) √5/13
(c) 12/5
(d) 12/13

Question. If sin A + sin² A=1 , then the value of cos² A + cos² A  is     
(a) – 1
(b) 2
(c) 0
(d) 1

Question. If cotθ = 7/8 , then the value of (1+sinθ)/(1-sinθ)/1+cosθ)(1-cosθ) is      
(a) 64/49
(b) 7/8
(c) 8/7
(d) 49/64

Question. If sin α =1/√2 and tan β = 1, then the value of cos (α+β) is     
(a) 3
(b) 1
(c) 2
(d) 0

Question. The value of cos 48° – sin 42° is      
(a) 0
(b) 1
(c) √2
(d) 1/2

Question. If 2sin²θ =√3, then the value of θ   
(a) 60°
(b) 45°
(c) 0°
(d) 30°

Question. Choose the correct option. Justify your choice.(sec A + tan A) (1 – sin A)   
(a) cos A
(b) sec A
(c) sin A
(d) cosec A

Question. sin² A + sin² A tan² A =   
(a) tan² A
(b) cos² A
(c) None of these
(d) sin² A

Question. If A, B and C are interior angles of a triangle ABC, then the value of tan(B+C)/2 is     
(a) cot A/2
(b) None of these
(c) tan A/2
(d) sin A/2

Question. If ΔPQR is right angled at Q, then the value of sin (P + R) is     
(a) 1/2
(b) 1
(c) √2
(d) 0

Question. (sec θ +cosθ ) (secθ – cos θ) =   
(a) tan²θ + cos²
(b) tan²θ – cos²θ
(c) tan²θ +sin²θ
(d) tan²θ -sin² θ

Question. Choose the correct option and justify your choice: 2tan 30°/1-tan²30°   
(a) cos60°
(b) sin 30°
(c) sin 60°
(d) tan 60°

Question. If 5 tan θ = 3, then what is the value of (5sin θ -3 cos θ/4sin θ +3cos θ)  ?     
(a) 0
(b) 1
(c) 2
(d) 3

Question. The value of sin 60° ⋅ cos 30° + sin 30° ⋅ cos 60° is     
(a) 0
(b) 1
(c) 2
(d) 8

Question. Value of cos 0° ⋅ cos 30° ⋅ cos 45° ⋅ cos 60° ⋅ cos 90° is     
(a) 0
(b) 1
(c) 2
(d) 9

Question. Evaluate: 4 sin² 60° + 3 tan² 30° – 8 sin 45° cos 45°       
(a) 0
(b) 1
(c) 2
(d) 5

Question. The value of (sin²θ +1/1 +tan² θ) =     
(a) 0
(b) 1
(c) 2
(d) 5

Question. The value of sin 60° cos 30° + sin 30° cos 60° is     
(a) 1
(b) 2
(c) 11
(d) 0

Question. 2 tan² 45° + cos² 30° – sin² 60° equals     
(a) 1
(b) 2
(c) 5
(d) 6

Question. If sin θ = x and sec θ = y, then the value of cot θ is     
(a) xy
(b) 2xy
(c) 1/ xy
(d) x + y

Question. If (1 + cos A)(1 – cos A) = 3/ 4 , the value of sec A is     
(a) 2
(b) –2
(c) ±2
(d) 0

Question. The value of (1 + tan² θ)(1 – sin θ)(1 + sin θ) =     
(a) 0
(b) 1
(c) 2
(d) None of these

Question. If 15 cot A = 8, then the value of cosec A is     
(a) 15/ 12
(b) 13/ 15
(c) 4/ 15
(d) 17/ 15

Question. If triangle ABC is right angled at C, then the value of sec (A + B) is     
(a) 0 
(b) 1
(c) 2/√3
(d) not defined

Question. Evaluate: sin30° + tan 45° – cosec 60°/sec 30° + cos60° + cot 45°   
(a) 3 √3 + 2/3√3 -2
(b) 3 √3/−4/ 3√3 +4
(c) 3√3/ + 3 √3 − 9 
(d) None of these

Question. If tan(A + B) = √3 and tan(A – B) = 1/√3 , A > B, then the value of A is     
(a) A = 30°
(b) A = 60°
(c) A = 90°
(d) A = 45°

Question. If sin θ = cos θ, then find the value of 2 tan θ + cos² θ.     
(a) 2 /3
(b) 3 /4
(c) 5 /2
(d) 0 

Question. The value of x such that ² cosec² 30° + x sin² 60° – 3/ 4 tan² 30° = 10, is     
(a) 1
(b) 2
(c) 3
(d) 5

Question. If tan A = 5/12 , then (sin A + cos A) ⋅ sec A is equal to     
(a) 11/ 12 
(b) 13/ 12
(c) 12 /19
(d) 17 /12

Question. If sin θ + cos θ = √2 cos θ, (θ ≠ 90°) then the value of tan θ is   
(a) √2 −1
(b) √2 +1
(c) √2
(d) − √2

Question. If tan θ + cot θ = 2, the value of √tan² θ + cot² θ is     
(a) 2
(b) 2
(c) 3
(d) 3

Question. ABC is right-angled triangle, right-angled at B. If BC = 7 cm and AC – AB = 1 cm, then cos A + sin A equals     
(a) 31/ 25
(b) 51/ 61
(c) 17 /39
(d) 51/ 53

Question. The value of cos sin cos sin30° + sin 60°/1 + cos 60° +sin 30°   is       
(a) √3 /2
(b) 2/ √3
(c) 1/ √2
(d) 0

Question. ABC is a triangle right angled at C and AC = √3 BC. Then ∠ABC =     
(a) 30°
(b) 60°
(c) 90°
(d) 0°

Question. The value of 5 cos²60 ° + 4sec² 30° − tan² 45°/sin2 30° + cos² 30° is     
(a) 32/ 35
(b) 14/ 55
(c) 67 /12
(d) 19/ 33

Question. The value of 3sin 30° +  4 cos ²45° − cot² 30°/cos² 30° + sin²30° is     
(a) 1/ 2
(b) 1/ 3
(c) 2/ 5
(d) 3/ 8

Question. Given sin (A – B) = √3/ 2 and cos (A + B) = √3/ 2 . Then A and B respectively are     
(a) 30°, 45°
(b) 45°, –15°
(c) 60°, 45°
(d) None of these

Question. The value of (sin 30° + cos 60°)   
(a) 1
(b) 2
(c) 0
(d) None of these

Question. The value of sin ⁶ θ + cos6 θ + 3sin² θ cos² θ is   
(a) 0
(b) 1
(c) 2
(d) 1/ 4

Question. The value of (sin⁴θ – cos⁴θ + 1) cosec²θ is   
(a) 0
(b) 1
(c) 2
(d) 5

Question. If cos A = 4/ 5 , then sin A and sec A respectively are   

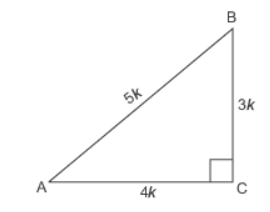
(a) 3/ 4 , 4/3
(b) 5/ 3 , 3/ 4
(c) 3 /5 , 5 /4  
(d) None of these

Question. If 4 tan θ = 3, then the value of 4 sin θ − cos θ /4 sin θ + cos θ  is   
(a) 1/ 2
(b) 1/ 3
(c) 1/ 4 
(d) 1/ 5

Question. If tan A = n tan B and sin A = m sin B, then cos² A =     
(a) m^2 − 1/n² − 1
(b) m² + 1/n² + 1
(c) 1 − m²/1 + m²
(d) 1+ m² /1 − m²

Question. Given that sin a = √3/ 2 and cos b = 0, then the value of β – α is     
(a) 0°
(b) 90°
(c) 60°
(d) 30°

Question. The angle of depression of a car standing on the ground, from the top of a 75 m high tower is 30°. The distance of the car from the base of the tower (in m) is:   
(a) 25 √3
(b) 50 √3
(c) 75 √3
(d) 150

Question. In the given figure, the angles of depressions from the observing positions O1 and O2 respectively of the object A respectively are   

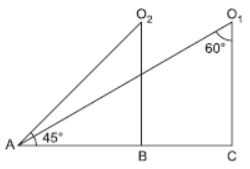
(a) 30°, 45°
(b) 45°, 60°
(c) 60°, 75°
(d) 60°, 30°

Question. A pole of 6 m high casts a shadow 2 √3 m long, then sun’s elevation is     
(a) 60°
(b) 45°
(c) 30°
(d) 90°

Question. At some time of the day, the length of the shadow of a tower is equal to height. Then the sun’s altitude at that time is   
(a) 30°
(b) 60°
(c) 90°
(d) 45°

In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.

Question. Assertion (A): If the angle of elevation of Sun, above a perpendicular line (tower) decreases, then the shadow of tower increases.   
Reason (R): It is due to decrease in slope of the line of sight.

Question. Assertion (A): When we move towards the object, angle of elevation decreases.     
Reason (R): As we move towards the object, it subtends large angle at our eye than before.

Question. In the following questions, a statement of assertion (A) is followed by a statement reason (R). Choose the correct choice as:  
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
1. Assertion (A): In a right-angled triangle, if tan θ = 3/ 4 , the greatest side of the triangle is 5 units.
Reason (R): (Greatest side)² = (Hypotenuse)² = (Perpendicular)² + (Base)².
Assertion (A): In a right-angled triangle, if cos θ =- 1/ 2 and sin θ = √3/ 2  , then tan θ = √3 . Reason (R): sinθ cos θ 

(a) If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
(b) If both Assertion and Reason are correct, but Reason is not the correct explanation of Assertion.
(c) If Assertion is correct but Reason is incorrect.
(d) If Assertion is incorrect but Reason is correct.

Question. Assertion: In a right angled triangle, if tan θ = 3/ 4 , the greatest side of the triangle is 5 units.
Reason: (greatest side)² = (hypotenuse)² = (perpendicular)² + (base)².

Question. Assertion : In a right angled triangle, if cos θ = 1/ 2 and sin θ = √3/ 2 , then tan θ = √3
Reason: tan θ = sinθ/ cos θ 

One Word Questions :

Question. If cos³θ =1 , then find the value of θ .

Question. If, A, B and C are the angles of a triangle, then find the value of tan (A + B)/2 in terms of angle C.

Question. If sin 3θ = cos 4θ , then find the value of 7θ .

Question. If sec²θ (1+ sinθ )(1− sinθ ) = k , then find the value of k.

Question. If CosA 3/5 ,then find the value of tan2 A− sec² A .

Question. Find the value of sin 20⁰ sin 70⁰ − cos 20⁰ cos 70⁰

Question. If sin θ = 3/5 , then find the value of 5cosθ ×sinθ .

Question. If tanθ = 12/5 then find the value of 13 sinθ/3 .

Question. Find the value of cos ecAsec(900 − A) − cot Atan(900 − A).

Question. Find the value of sin θ – sin3 θ/cos θ – cos3 θ .

Question. If tanθ = 4, then find the value of 1/10 (tan² θ + 2sec² )

Question. If sin θ = 1/3 , then find the value of 2cosec²θ + cot2θ + 1 .

Question. If cos² 20°/2(sin² 59° sin2 31°) 2/k , then find the value of k.

Question. If tan α = 1/√3 and sin β = 1/√2 , find the value of α +β .

Question. If cosec² and cotθ = √3k , then find the value of k.

Question. If cosec² θ = 3/2 , then find the value of 2(cosec²θ + cot²θ ) .

Question. Find the value of tan 50 × tan 300 × 4 tan 85⁰

Question. If tanθ tan 45⁰ = 1, then find the value of θ

Question. If cos θ = 3/2 , then find the value of 8sec²θ + tan2θ + 1 .

Question. If 1+ 2sin²θ cos²θ = sin²θ + cos²θ + 4k sin²θ cos²θ , then find the value of k.