VBQs Complex Numbers And Quadratic Equations Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Complex Numbers And Quadratic Equations Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Complex Numbers And Quadratic Equations VBQs Class 11 Mathematics
Question. If z1 = √2 [cosπ/4 + isinπ/4] and z2 = √3 [cosπ/3 + isinπ/3] then |z1 z2| is equal to m . Value of m is
(a) 6
(b) 3
(c) 2
(d) 5
Answer
A
Question. If a + ib = x + iy, then possible value of a – ib is
(a) x2 + y2
(b) √x2 + y2
(c) x + iy
(d) x – iy
Answer
D
Question. Value of i592 + i590 + i588 + i586 + i584/i582 + i580 + i578 + i576 + i574 – 1 is
(a) –2
(b) 0
(c) –1
(d) 1
Answer
A
Question.
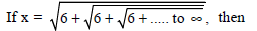
(a) x is an irrational number
(b) 2 < x < 3
(c) x = 3
(d) None of these
Answer
C
Question. If α, β are the roots of (x – a) (x – b) = c, c ≠ 0, then the roots of (x – α) (x – β) + c = 0 shall be
(a) a, c
(b) b, c
(c) a, b
(d) a + c, b + c
Answer
C
Question. The roots of the equation 4x – 3 . 2x + 3 + 128 = 0 are
(a) 4 and 5
(b) 3 and 4
(c) 2 and 3
(d) 1 and 2
Answer
B
Question. Simplify the complex numbers given in column-I and match with column-II

Codes:
A B C D
(a) 3 1 4 2
(b) 3 4 1 2
(c) 2 4 1 3
(d) 2 1 4 3
Answer
C
Question. If z = 7 – i/3 – 4i then |z|14 =
(a) 27
(b) 27 i
(c) –27
(d) –27 i
Answer
A
Question. If (1 – i)n = 2n, then the value of n is
(a) 1
(b) 2
(c) 0
(d) None of these
Answer
C
Question. The modulus and amplitude of 1 + 2i/1 –(1 –i) are
(a) √2 and π/6
(b) 1 and 0
(c) 1 and π/3
(d) 1 and π/4
Answer
B
Question. If the equation (m – n)x2+ (n – l)x + l – m = 0 has equal roots, then l, m and n satisfy
(a) 2l = m + n
(b) 2m = n + l
(c) m = n + l
(d) l = m + n
Answer
B
Question. If z = 2 –3i, then value of z2 – 4z + 13 is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. If | z – 4 | < | z – 2 |, its solution is given by
(a) Re(z) > 0
(b) Re(z) < 0
(c) Re(z) > 3
(d) Re(z) > 2
Answer
C
Question. A value of k for which the quadratic equation x2 – 2x(1 + 3k) + 7(2k + 3) = 0 has equal roots is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
B
Question. If the equations k (6x2 + 3) + rx + 2x2 – 1 = 0 and 6k (2x2 – 1) + px + 4x2 + 2 = 0 have both roots common, then the value of (2r – p) is :
(a) 0
(b) 1/2
(c) 1
(d) None of these
Answer
A
Question. The equation whose roots are twice the roots of the equation, x2 – 3x + 3 = 0 is:
(a) 4x2 + 6x + 3 = 0
(b) 2x2 – 3x + 3 = 0
(c) x2 – 3x + 6 = 0
(d) x2 – 6x + 12 = 0
Answer
D
Question. If α, β are the roots of the equation ax2 + bx + c = 0, then α/aβ + b + β/aα + b =
(a) 2/a
(b) 2/b
(c) 2/c
(d) –2/a
Answer
D
Question. The complex number z which satisfies the condition l i+ z/i – z l = 1 lies on
(a) circle x2 + y2 = 1
(b) the x-axis
(c) the y-axis
(d) the line x + y = 1
Answer
B
Question. If Z = i – 1/cosπ/3 + i sinπ/3 ,then polar form of Z is
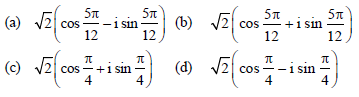
Answer
B
Question. If p and q are the roots of the equation x2+px+q = 0, then
(a) p = 1, q = –2
(b) p = 0, q = 1
(c) p = –2, q = 0
(d) p = – 2, q =1
Answer
A
Question. If z1 = 6 + 3i and z2 = 2 – i, then z1/z2 is equal to
(a) 1/5(9 + 12i )
(b) 9 + 12i
(c) 3 + 2i
(d) 1/5(12 + 9i)
Answer
A
Question. If α,β are the roots of ax2 + bx + c = 0, then αβ2 + α2β + αβ equals
(a) c(a–b)/a2
(b) 0
(c) –bc/a2
(d) abc
Answer
A
Question. The value of i4n+1 – i4n – 1 /2 is
(a) i
(b) 2i
(c) –i
(d) –2i
Answer
A
Question.
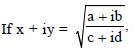
, then (x2 + y2)2 =
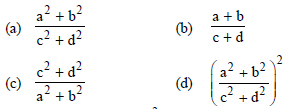
Answer
A
Question. If z = 5i(–3/5i) , then z is equal to 3 + bi. The value of ‘b’ is
(a) 1
(b) 2
(c) 0
(d) 3
Answer
C
Question. If α, β are the roots of the equation (x – a) (x – b) = 5, then the roots of the equation (x – α) (x – β) + 5 = 0 are
(a) a, 5
(b) b, 5
(c) a, α
(d) a, b
Answer
D
Question. The amplitude of sinπ/5 + i(1 – cosπ /5) is
(a) π/5
(b) 2π/5
(c) π/10
(d) π/15
Answer
C
Question. If the roots of the equation ax2 + bx + c = 0 are α, β, then the value of αβ2 + α2β + αβ will be
(a) c(a – b )/a2
(b) 0
(c) – bc/a2
(d) None of these
Answer
A
Question. If the two roots of the equation, (a – 1)(x4 + x2 + 1) + (a + 1)(x2 + x + 1)2 = 0 are real and distinct, then the set of all values of ‘a’ is :
(a) (0, 1/2)
(b) ( – 1/2)∪(0, 1/2)
(c) ( – 1/2, 0)
(d) (-∞ , -2)∪(2, ∞)
Answer
B
Question. If 2 + 3i is one of the roots of the equation 2x3 – 9x2 + kx – 13 = 0, k ∈ R, then the real root of this equation :
(a) exists and is equal to – 1/2.
(b) exists and is equal to 1/2.
(c) exists and is equal to 1.
(d) does not exist.
Answer
B
Question. The sum of the roots of the equation, x2 + |2x – 3| – 4 = 0, is:
(a) 2
(b) – 2
(c) √2
(d) – √2
Answer
C
Question. If p and q are non- ero real numbers and α3 + β3 = – p,αβ = q, then a quadratic equation whose roots are α2/β , β2/α is :
(a) px2 – qx + p2 = 0
(b) qx2 + px + q2 = 0
(c) px2 + qx + p2 = 0
(d) qx2 – px + q2 = 0
Answer
B
Question. Let p, q, r ∈ R and r > p > 0. If the quadratic equation px2 + qx + r = 0 has two complex roots α and β, then |α| + |β| is
(a) equal to1
(b) less than 2 but not equal to 1
(c) greater than 2
(d) equal to 2
Answer
C
Question. If 5, 5r, 5r2 are the lengths of the sides of a triangle, then r cannot be equal to:
(a) 3/4
(b) 5/4
(c) 7/4
(d) 3/2
Answer
C
Question. Let α, b ∈ R, α ≠ 0 be such that the equation, αx2 – 2bx + 5 = 0 has a repeated root α, which is also a root of the equation, x2 – 2bx – 10 = 0. If β is the other root of this equation, then α2 + β2 is equal to :
(a) 25
(b) 26
(c) 28
(d) 24
Answer
A
Question. If the sum of the square of the roots of the equation x2 – (sin α – 2)x – (1 + sin α) = 0 is least, then a is equal to
(a) π/6
(b) π/4
(c) π/3
(d) π/2
Answer
D
Question. Sachin and Rahul attempted to solve a quadratic equation. Sachin made a mistake in writing down the constant term and ended up in roots (4,3). Rahul made a mistake in writing down coefficient of x to get roots (3,2). The correct roots of equation are :
(a) 6, 1
(b) 4, 3
(c) – 6, – 1
(d) – 4, – 3
Answer
A
Question. If (1+i / 1-i)x = 1 then
(a) x = 2n +1 , where n is any positive integer
(b) x = 4n , where n is any positive integer
(c) x = 2n , where n is any positive integer
(d) x = 4n +1 , where n is any positive integer.
Answer
B
Question. If z and ω are two non- zero complex numbers such that |zω| =1 and Arg(z) – Arg(ω) = π/2 then z̅ω, is equal to
(a) – 1
(b) 1
(c) – i
(d) i
Answer
A
Question. If α and β are roots of the equation x2 + px + 3p / 4 = 0 such that | α -β |= 10, then p belongs to the set :
(a) {2, – 5}
(b) {– 3, 2}
(c) {– 2, 5}
(d) {3, – 5}
Answer
C
Question. If a complex number z statisfies the equation z + √2 | z +1| +i = 0 , then | z | is equal to :
(a) 2
(b) √3
(c) √5
(d) 1
Answer
C
Question. If the roots of the equation bx2 + cx + α = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is :
(a) less than 4αb
(b) greater than – 4αb
(c) 1ess than – 4αb
(d) greater than 4αb
Answer
B
Question. If the difference between the roots of the equation x2 + ax + 1 = 0 is less than √5 , then the set of possible values of a is
(a) (3,∞)
(b) (-∞,-3)
(c) (– 3, 3)
(d) (-3, ∞)
Answer
C
Question. For all complex numbers of the form 1 + iα, α ∈ R , if z2 = x + iy, then
(a) y2 – 4x + 2 = 0
(b) y2 + 4x – 4 = 0
(c) y2 – 4x – 4 = 0
(d) y2 + 4x + 2 = 0
Answer
B
Question. If z1, z2 and z3, z4 are 2 pairs of complex conjugate numbers, then arg(z1/z4) + arg(z2/z3) equals:
(a) 0
(b) π/2
(c) 3π/2
(d) π
Answer
A
Question. All the values of m for which both roots of the equation x2 – 2mx + m2 – 1 = 0 are greater than – 2 but less than 4, lie in the interval
(a) -2 < m < 0
(b) m > 3
(c) -1 < m < 3
(d) 1 < m < 4
Answer
C
Question. If one root of the equation x2 + px +12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots , then the value of ‘q’ is
(a) 4
(b) 12
(c) 3
(d) 49/4
Answer
D
Question. The value of ‘α’ for which one root of the quadratic equation (α2 – 5α + 3)x2 + (3α -1)x + 2 = 0 is twice as large as the other is
(a) – 1/3
(b) 2/3
(c) – 2/3
(d) 1/3
Answer
B
Question. Product of real roots of the equation t2 x2 + | x | + 9 = 0
(a) is always positive
(b) is always negative
(c) does not exist
(d) none of these
Answer
A
Question. If α and β are the roots of the equation x2 + px + 2 = 0 and 1/α and 1/β are the roots of the equation 2x2 + 2qx + 1 = 0, then (α – 1/α)(β – 1/β)(α + 1/β)(β + 1/α) is equal to :
(a) 9/4 (9 + q2)
(b) 9/4 (9 – q2)
(c) 9/4 (9 + p2)
(d) 9/4 (9 – p2)
Answer
D
Question. Let z ≠ – i be any complex number such that z–i / z+i is a purely imaginary number. Then Z + z is :
(a) zero
(b) any non- zero real number other than 1.
(c) any non- zero real number.
(d) a purely imaginary number.
Answer
C
Question. The set of all real values of λ for which the quadratic equations, (λ2 +1)x2 – 4λx + 2 = 0 always have exactly one root in the interval (0, 1) is :
(a) (0, 2)
(b) (2, 4]
(c) (1, 3]
(d) (–3, –1)
Answer
C
Question. If ƒ(x) is a quadratic expression such that ƒ(a) + ƒ(b) = 0, and – 1 is a root of ƒ(x) = 0, then the other root of ƒ(x) = 0 is
(a) – 5/8
(b) – 8/5
(c) 5/8
(d) 8/5
Answer
D
Question. If α, β ∈ C are the distinct roots, of the equation x2 – x +1 = 0 , then α101 + β107 is equal to :
(a) 0
(b) 1
(c) 2
(d) – 1
Answer
B
Question. Let Z1 and Z2 be any two complex number.
Statement 1: |Z1 – Z2| ≥ |Z1| – |Z2|
Statement 2: |Z1 + Z2| ≤ |Z1| + |Z2|
(a) Statement 1 is true, Statement 2 is true, Statement 2 is a correct explanation of Statement 1.
(b) Statement 1 is true, Statement 2 is true, Statement 2 is not a correct explanation of Statement 1.
(c) Statement 1 is true, Statement 2 is false.
(d) Statement 1 is false, Statement 2 is true.
Answer
B
Question. The number of complex numbers such that |z – 1| = |z + 1| = |z – i| equals
(a) 1
(b) 2
(c) ∝
(d) 0
Answer
A
Question. If ω(≠1) is a cube root of unity, and (1+ω)7 = A+ Bω. Then (A, B) equals
(a) (1, 1)
(b) (1, 0)
(c) (–1, 1)
(d) (0, 1)
Answer
A
Question. If | z + 4 | ≤ 3, then the maximum value of | z + 1 | is
(a) 6
(b) 0
(c) 4
(d) 10
Answer
A
Question. The polar form of the complex number (i25)3 is
(a) cosπ/2 + isinπ/2
(b) cosπ/2 – isinπ/2
(c) cosπ/3 + isinπ/3
(d) cosπ/3 – isinπ/3
Answer
B
Question. If α, β are roots of the equation x2 – 5x + 6 = 0, then the equation whose roots are α + 3 and β + 3 is
(a) 2x2 – 11x 30 = 0
(b) –x2 +11x = 0
(c) x2 –11x + 30 = 0
(d) 2x2 – 5x + 30 = 0
Answer
C
Question. (x – iy) (3 + 5i) is the conjugate of (–6 – 24i), then x and y are
(a) x = 3, y = –3
(b) x = –3, y = 3
(c) x = –3, y = –3
(d) x = 3, y = 3
Answer
A
Question. If z = 1 + i, then the multiplicative inverse of z2 is (where, i = √–1 )
(a) 2i
(b) 1– i
(c) –i/2
(d) i/2
Answer
C
Question. What is the conjugate of
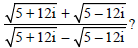
(a) –3i
(b) 3i
(c) 3/2 i
(d) – 3/2 i
Answer
C
Question. If |z | = 1, (z ≠ –1) and z = x + iy, then (z –1/z + 1) is
(a) purely real
(b) purely imaginary
(c) zero
(d) undefined
Answer
B
Question. If A.M. of the roots of a quadratic equation is 8/5 and A.M. of their reciprocals is 8/7 ,then the equation is
(a) 5x2 – 16x + 7 = 0
(b) 7x2 – 16x + 5 = 0
(c) 7x2 – 16x + 8 = 0
(d) 3x2 – 12x + 7 = 0
Answer
A
Question. Which of the following options defined ‘imaginary number’?
(a) Square root of any number
(b) Square root of positive number
(c) Square root of negative number
(d) Cube root of number
Answer
C
Question. If a and b are the odd integers, then the roots of the equation 2ax2 + (2a + b)x + b = 0, a ≠ 0, will be
(a) rational
(b) irrational
(c) non-real
(d) equal
Answer
A
Question. If c + i/c – i = a + ib, where a, b, c are real, then a2 + b2 is equal to:
(a) 7
(b) 1
(c) c2
(d) – c2
Answer
B
Question. If z = x + iy, z1/ 3 = a – ib, then x/a – y/b = k ( a2 – b2 ) where k is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Answer
D
Question. Simplify the complex numbers given in column-I and match with column-II
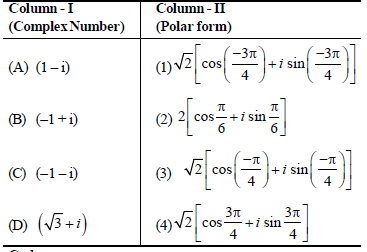
Codes:
A B C D
(a) 3 4 1 2
(b) 3 1 4 2
(c) 2 4 1 3
(d) 2 1 4 3
Answer
A
Question. If z = i–39, then simplest form of z is equal to a + i. The value of ‘a’ is
(a) 0
(b) 1
(c) 2
(d) 3
Answer
A
Question. |z1 + z2| = |z1| + |z2| is possible, if
(a) z2 = z¯1
(b) z2 = 1/z1
(c) arg(z1) = arg(z2)
(d) |z1| = |z2|
Answer
C
Question. If | z + 4 | ≤ 3, then the maximum value of | z + 1 | is
(a) 6
(b) 0
(c) 4
(d) 10
Answer
A
Question. If the roots of the equation a/x – a + b/x – b = 1 are equal in magnitude and opposite in sign, then
(a) a = b
(b) a + b = 1
(c) a – b = 1
(d) a + b = 0
Answer
D
Question. For the equation 3x2 + px + 3 = 0, p > 0, if one of the root is square of the other, then p is equal to
(a) 1/3
(b) 1
(c) 3
(d) 2/3
Answer
C
Question. Simplify the complex numbers given in column-I and match with column-II

Codes:
A B C D
(a) 1 2 3 4
(b) 4 3 1 2
(c) 4 1 3 2
(d) 2 3 1 4
Answer
B
Question. (1 + i)8 + (1 – i)8 equal to
(a) 28
(b) 25
(c) 24 cos π/4
(d) 28 cos π/8
Answer
B
Question. If (1 + i)3/(1 – i)3 – (1 – i)3/(1 + i )3 = x + iy
(a) x = 0, y = –2
(b) x = –2, y = 0
(c) x = 1, y = 1
(d) x = –1, y = 1
Answer
A
Question. If (x + iy) (2 – 3i) = 4 + i, then
(a) x = c 14/13, y = 5/13
(b) x = 5/13, y = 14/13
(c) x = 14/13, y = 5/13
(d) x = 5/13, y = – 14/13
Answer
B
Question. 2x2 – (p + 1) x + (p – 1) = 0. If α – β = αβ, then what is the value of p?
(a) 1
(b) 2
(c) 3
(d) –2
Answer
B
Question. If z1 and z2 are two non-zero complex numbers such that | z1 + z2 | = | z1 | + | z2 | , then arg z1 – arg z2 is equal to
(a) π/2
(b) – π
(c) 0
(d) –π/2
Answer
C
Question. The modulus of the complex number z such that |z + 3 – i | = 1 and arg(z) = π is equal to
(a) 3
(b) 2
(c) 9
(d) 4
Answer
A
Question. The square root of i is
(a) ±1/√2(–1 + i )
(b) ±1/√2(1 + i )
(c) ±1/√2(1 – i )
(d) None of these
Answer
B
STATEMENT TYPE QUESTIONS
Question. Consider the following statements.
I. If z, z1, z2 be three complex numbers then zz¯ = |z|2
II. The modulus of a complex number z = a + ib is defined as |z| = √a2 + b2 .
III. Multiplicative inverse of z = 3 – 2i is 3/13 + 2/13i
Choose the correct option.
(a) Only I and II are correct.
(b) Only II and III are correct.
(c) Only I and III are correct.
(d) All I, II and III are correct.
Answer
D
Question. Consider the following statements
I. Additive inverse of (1 – i) is equal to –1 + i.
II. If z1 and z2 are two complex numbers, then z1 – z2 represents a complex number which is sum of z1 and additive inverse of z2.
III. Simplest form of 5 + √2i/1–√2i is 1 + 2√2 i.
Choose the correct option.
(a) Only I and II are correct.
(b) Only II and III are correct.
(c) I, II and III are correct.
(d) I, II and III are incorrect.
Answer
C
Question. Statement – I : Roots of quadratic equation x2 + 3x + 5 = 0 is x = –3 ± i√11/2.
Statement – II : If x2 – x + 2 = 0 is a quadratic equation, then its roots are 1 ± i√7/2.
(a) Statement I is correct
(b) Statement II is correct
(c) Both are correct
(d) Both are incorrect
Answer
A
Question. Consider the following statements.
I. Modulus of 1+i /1–i is 1.
II. Argument of 1+i /1–i is π/2
Choose the correct option.
(a) Only I is correct.
(b) Only II is correct.
(c) Both are correct.
(d) Both are incorrect.
Answer
C
Question. Consider the following statements.
I. Representation of z = x + iy in terms of r and θ is called polar form of the complex number.
II. arg (z1/z2)= arg (z1) – arg (z2)
Choose the correct option.
(a) Only I is incorrect.
(b) Only II is correct.
(c) Both I and II are incorrect.
(d) Both I and II are correct.
Answer
D