VBQs Probability Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Probability Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Probability VBQs Class 11 Mathematics
Question: In a large metropolitan area, the probabilities are 0.87, 0.36, 0.30 that a family (randomly chosen for a sample survey) owns a colour television set, a black and white television set or both kinds of sets. What is the probability that a family owns either anyone or both kinds of sets?
(a) 0.95
(b) 0.93
(c) 0.98
(d) None of these
Answer
B
Question: Suppose an integer from 1 through 1000 is chosen at random, find the probability that the integer is a multiple of 2 or a multiple of 9.
(a) 0.556
(b) 0.557
(c) 0.559
(d) None of these
Answer
A
Question: Given two events A and B. If odds against A are as 2 : 1 and those in favour of A ∪ B are as 3 : 1, then
(a) 1/2 ≤ P (B) ≤ 3/4
(b) 5/12 ≤ P (B) ≤ 3/4
(c) 1/4 ≤ P (B) ≤ 3/5
(d) None of these
Answer
B
Question: If P (A∪ B) = P (A ∩ B for any two events A and B, then
(a) P (A)= P(B)
(b) P (A) > P (B)
(c) P (A)< P (B)
(d) None of these
Answer
A
Question: If P(A)1/3, P(B )= 1 /2 and P (A ∪ B) = 5/6, then events A and B are
(a) mutually exclusive
(b) independent as well as mutually exhaustive
(c) independent
(d) dependent only on
Answer
A
Question: In shuffling a pack of playing cards, four are accidently dropped. The probability that missing cards should be one from each suit, is
(a) 1256
(b) 1/270725
(c) 2197/20825
(d) None of these
Answer
C
Question: Given, P (A) =3/5 and P(B) = 1/5. Find P (A or B), if A and B are mutually exclusive events.
(a) 2/5
(b) 3/5
(c) 4/5
(d) 1/5
Answer
C
Question: If A and Bare any two events, then P (Α̅ ∩ B ) is equal to
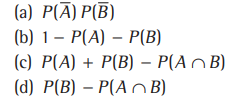
Answer
D
Question: If E and F are events such that P (E) = 1/4,P(F)=1/2 and P(E and F) = 1/8 Find (i) P(E or F) (ii) P(not E and not F).
(a) 1/8,7/8
(b) 5/8,3/8
(c) 1/, 6/7
(d) None of these
Answer
B
Question: A card is drawn from a deck of 52 cards. Find the probability of getting a king or a heart or a red card.
(a) 5/13
(b) 7/13
(c) 25/52
(d) None of these
Answer
B
Question: From the employees of a company, 5 persons are selected to represent them in managing committee of the company. Particulars of five persons are as follows
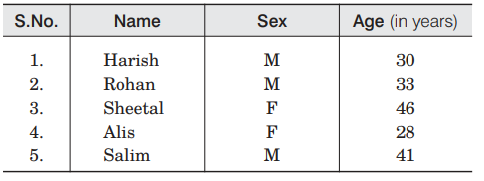
A person is selected at random from this group to act as a spokes person. What is the probability that the spokes person will be either male or over 35yr?
(a) 4/5
(b) 1/5
(c) 3/5
(d) None of these
Answer
A
Question: If P( A ∩ B)=1/3,p(A∪B) = 5/6 and P (A ) =1/2 , then which one of the following is correct?
(a) A and B are independent events
(b) A and B are mutually exclusive events
(c) P (A) = P (B)
(d) None of the above
Answer
A
Question: In class XI of a school, 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
(a) 0.5
(b) 0.6
(c) 0.65
(d) None of these
Answer
B
Question: An experiment yields 3 mutually exclusive and exhaustive events A, B and C. If P(A)=2P(B)=3P(C), then P (A ) is equal to
(a) 1/11
(b) 2/11
(c) 3/11
(d) 6/11
Answer
D
Question: If A and B are arbitrary events, then
(a) P (A ∩ B) ≤ P(A) +P(B)
(b) P (A ∪ B) ≤ p(A)+p(B)
(c) P (A∩B )= P(A) + P(B)
(d) None of these
Answer
B
Question: The probability that at least one of the events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.2, then P (Α̅ ) +P (Β̅) is
(a) 0.4
(b) 0.8
(c) 1.2
(d) 1.6
Answer
C
Question: If the probabilities for A to fail in an examination is 0.2 and that for B is 0.3, then the probability that either A or B fails is
(a) >.5
(b) .5
(c) ≤ .5
(d) 0
Answer
B
Question: A man and his wife appear for an interview for two posts. The probability of the man’s selection is 1/5 and that of his wife’s selection is 1/7. The probability that at least one of them is selected, is
(a) 9/35
(b) 12/35
(c) 2/7
(d) 11/35
Answer
D
Question: Given two mutually exclusive events A and B such that P (A ) = 0.45 and P (B ) = 0.35, P(A ∩ B) is equal to
(a) 63/400
(b) 0.8
(c) 63/200
(d) 0
Answer
D
Question: If A and B are events of the same experiments with P (A) = 0.2, P(B ) = 0.5, then maximum value of p(A’∩ B) is
(a) 0.2
(b) 0.5
(c) 0.63
(d) 0.25
Answer
B
Question: A natural number x is chosen at random from the first 100 natural numbers. The probability that x + 100/x>50 is
(a) 1/10
(b) 11/50
(c) 11/20
(d) None of these
Answer
C
Question: Three letters are written to there different persons and addresses on the three envelopes are also written. Without looking at the addresses, the letters are kept in these envelopes. The probability that all the letters are not placed into their right envelopes is
(a) 1/2
(b) 1/3
(c) 1/6
(d) 5/6
Answer
B
Question: A bag contains 8 red and 5 white balls. Three balls are drawn at random. Find the probability that
I. All the three balls are white
II. All the three balls are red
III. One ball is red and two balls are white

Answer
B
Question: Three critics review a book. Odds in favour of the book are 5 : 2, 4 : 3 and 3 : 4, respectively, for the three critics. The probability that majority are in favour of the book is
(a) 35/49
(b) 125/343
(c) 164/343
(d) 209/343
Answer
D
Question: A class consists of 80 students, 25 of them are girls and 55 are boys. If 10 of them are rich and the remaining are poor and also 20 of them are intelligent, then the probability of selecting an
intelligent rich girl is
(a) 5/128
(b) 25/128
(c) 5/512
(d) None of the above
Answer
C
Question: The chance of an event happening is the square of the chance of a second event but the odds against the first are the cube of the odds against the second. The chances of the events are
(a) p1 = 1 9/
(b) p1 = 116 /
(c) p2 = 1 3/
(d) p2 = 1 4
Answer
(A,C)