VBQs Sequences and Series Class 11 Mathematics with solutions has been provided below for standard students. We have provided chapter wise VBQ for Class 11 Mathematics with solutions. The following Sequences and Series Class 11 Mathematics value based questions with answers will come in your exams. Students should understand the concepts and learn the solved cased based VBQs provided below. This will help you to get better marks in class 11 examinations.
Sequences and Series VBQs Class 11 Mathematics
Question. If sixth term of a H. P. is 1/61 and its tenth term is 1/105 then the first term of that H.P. is
(a) 1/28
(b) 1/39
(c) 1/6
(d) 1/17
Answer
C
Question. If in a series Sn = an2 + bn + c, where Sn denotes the sum of n terms, then
(a) The series is always arithmetic
(b) The series is arithmetic from the second term onwards
(c) The series may or may not be arithmetic
(d) The series cannot be arithmetic
Answer
B
Question. The sum to infinite term of the series 1+2/3 +6/32 +10/33 + 14/34 + … is
(a) 3
(b) 4
(c) 6
(d) 2
Answer
A
Question. A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then the common ratio is
(a) 5
(b) 1
(c) 4
(d) 3
Answer
C
Question. The first two terms of a geometric progression add up to 12. the sum of the third and the fourth terms is 48. If the terms of the geometric progression are alternately positive and negative, then the first term is
(a) –4
(b) –12
(c) 12
(d) 4
Answer
B
Question. What is the sum of terms equidistant from the beginning and end in an A.P. ?
(a) First term – Last term
(b) First term × Last term
(c) First term + Last term
(d) First term ÷ Last term
Answer
C
Question. Sum of n terms of series 1.3+3.5+5.7+………. is
(a) 1/3 n(n + 1)(2n + 1) − n
(b) 3/2 n(n + 1)(2n + 1) − n
(c) 4/5 n(n + 1)(2n + 1) − n
(d) 2/3 n(n + 1)(2n + 1) − n
Answer
D
Question. If the arithmetic mean of two numbers be A and geometric mean be G, then the numbers will be
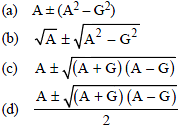
Answer
C
Question. If 5 (3a – 1 + 1), (62a – 3 +2) and 7(5a – 2 + 5) are in AP, then what is the value of a?
(a) 7
(b) 6
(c) 5
(d) None of these
Answer
D
Question. The A. M. between two positive numbers a and b is twice the G. M. between them. The ratio of the numbers is
(a) (√2 + 3) : (√2 – 3)
(b) (2 + √3 ) : (2 – √3 )
(c) (√3 + 1) : (√3 – 1)
(d) None of these
Answer
B
Question. There are four arithmetic means between 2 and –18. The means are
(a) –4, –7, –10, –13
(b) 1, –4, –7, –10
(c) –2, –5, –9, –13
(d) –2, –6, –10, –14
Answer
D
Question. If the jth term and kth term of an A.P. are k and j respectively, the ( k + j) th term is
(a) 0
(b) 1
(c) k + j + 1
(d) k + j –1
Answer
A
Question. The harmonic mean of a/1 – ab and a/1 + ab is
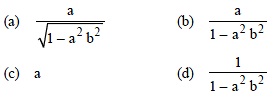
Answer
C
Question. If sum of the infinite G.P. is 4/3 and its first term is 3/4 then its common ratio is :
(a) 7/16
(b) 9/16
(c) 1/9
(d) 7/9
Answer
A
Question. Let x be one A.M and g1 and g2 be two G.Ms between y and z. What is g13 + g23 equal to ?
(a) xyz
(b) xy2z
(c) xyz2
(d) 2 xyz
Answer
D
Question. If 1, x, y, z, 16 are in geometric progression, then what is the value of x + y + z ?
(a) 8
(b) 12
(c) 14
(d) 16
Answer
C
Question. 51+x + 51–x, a/2 , 52x + 5–2x are in A.P., then the value of a is:
(a) a < 12
(b) a ≤ 12
(c) a ≥ 12
(d) None of these
Answer
D
Question. If the sequence is defined by an = n(n + 2), then match the columns.

Codes
A B C D E
(a) 4 3 5 2 1
(b) 4 2 5 3 1
(c) 1 3 2 5 4
(d) 3 4 5 1 2
Answer
A
Question. If the sum of a certain number of terms of the A.P. 25, 22, 19, …….. is 116. then the last term is
(a) 0
(b) 2
(c) 4
(d) 6
Answer
C
Question. The product of first nine terms of a GP is, in general, equal to which one of the following?
(a) The 9th power of the 4th term
(b) The 4th power of the 9th term
(c) The 5th power of the 9th term
(d) The 9th power of the 5th term
Answer
D
Question. The first term of an infinite G.P. is 1 and each term is twice the sum of the succeeding terms. then the sum of the series is
(a) 2
(b) 3
(c) 3/2
(d) 5/2
Answer
C
Question. Consider an infinite geometric series with first term a and common ratio r. If its sum is 4 and the second term is 3/4 ,then :
(a) a = 4/7, r = 3/7
(b) a = 2, r = 3/8
(c) a = 3/2, r = 1/2
(d) a = 3, r = 1/4
Answer
D
Question. If the sum of the first 2n terms of 2, 5, 8, ……. is equal to the sum of the first n terms of 57, 59, 61……., then n is equal to
(a) 10
(b) 12
(c) 11
(d) 13
Answer
C
Question. What is the sum of the first 50 terms of the series (1 × 3) + (3 × 5) + (5 × 7) + …. ?
(a) 1,71,650
(b) 26,600
(c) 26,650
(d) 26,900
Answer
A
Question. The sum of the first n terms of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 +… is n(n+1)2/2 when n is even. When n is odd the sum is
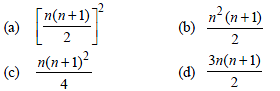
Answer
B
Question. If the 7th term of a H.P. is 1/10 and the 12th term is 1/25, then the 20th term is
(a) 1/37
(b) 1/41
(c) 1/45
(d) 1/49
Answer
D
Question. The first and eight terms of a G.P. are x–4 and x52 respectively. If the second term is xt, then t is equal to:
(a) –13
(b) 4
(c) 5/2
(d) 3
Answer
B
Question. The product of n positive numbers is unity, then their sum is :
(a) a positive integer
(b) divisible by n
(c) equal to n + 1/n
(d) never less than n
Answer
D
Question. The value of x + y + z is 15 if a, x, y, z, b are in A.P. while the value of 1/x+1/y+1/z is 5/3 if a, x, y, z, b are in H.P. Then the value of a and b are
(a) 2 and 8
(b) 1 and 9
(c) 3 and 7
(d) None of these
Answer
B
Question. If the nth term of an arithmetic progression is 3n + 7, then what is the sum of its first 50 terms?
(a) 3925
(b) 4100
(c) 4175
(d) 8200
Answer
C
Question. Let a, b, c, be in A.P. with a common difference d. Then e1/ c , eb / ac , e1/ a are in :
(a) G.P. with common ratio ed
(b) G.P with common ratio e1/d
(c) G.P. with common ratio ed /(b2 − d2 )
(d) A.P.
Answer
C
Question. In an AP. the pth term is q and the (p + q)th term is 0. Then the qth term is
(a) – p
(b) p
(c) p + q
(d) p – q
Answer
B
Question. Find the sum up to 16 terms of the series 13/1 + 13 + 23/1+3 + 13 + 23 + 33 /1+3+5+…
(a) 448
(b) 445
(c) 446
(d) None of these
Answer
C
Question. In a G.P. if (m + n)th term is p and (m – n)th term is q, then mth term is:
(a) p/q
(b) q/p
(c) pq
(d) √pq
Answer
D
Question. If a, b, c are in A.P. and a, b, d in G.P., then a, a – b, d – c will be in
(a) A.P.
(b) G.P.
(c) H.P.
(d) None of these
Answer
B
Question. Let a1, a2 , a3.……….. be terms of an A.P. If a1 + a2 +……..ap / a1 + a2 +……..aq = p2/q2, p ≠ q , then equals a6/a21
(a) 41/11
(b) 7/2
(c) 2/7
(d) 11/41
Answer
D
Question. If the pth, qth and rth terms of a G.P. are again in G.P., then which one of the following is correct?
(a) p, q, r are in A.P.
(b) p, q, r are in G.P.
(c) p, q, r are in H.P.
(d) p, q, r are neither in A.P. nor in G.P. nor in H.P.
Answer
A
Question. If S1,S2 and S3 denote the sum of first n1, n2 and n3 terms respectively of an A.P., then value of s1/n1(n2−n3) +s2/n2(n3−n1) + s3/n3(n1−n2)is
(a) 1/2
(b) 0
(c) −1/2
(d) 3/2
Answer
B
Question. The fifth term of the H.P., 2, 2.1/2 , 3.1/3 , ………………. will be

Answer
D
Question. The series ( √2 +1),1,(√2 −1) … is in :
(a) A.P.
(b) G.P.
(c) H.P.
(d) None of these
Answer
B
Question. If the sum of the first ten terms of an arithmetic progression is four times the sum of the first five terms, then the ratio of the first term to the common difference is :
(a) 1 : 2
(b) 2 : 1
(c) 1 : 4
Answer
A
Question. If A > 0, B > 0 and A + B = π/6 , then the minimum value of tanA + tanB is :
(a) √3 – √2
(b) 4 – 2√3
(c) 2/√3
(d) 2 – √3
Answer
B
Question. The sum of the 3rd and the 4th terms of a G.P. is 60 and the product of its first three terms is 1000. If the first term of this G.P. is positive, then its 7th term is :
(a) 7290
(b) 640
(c) 2430
(d) 320
Answer
D
Question. Three positive numbers form an increasing G. P. If the middle term in this G.P. is doubled, the new numbers are in A.P. then the common ratio of the G.P. is:
(a) 2 – √3
(b) 2 + √3
(c) √2 + √3
(d) 3 + √2
Answer
B
Question. Let x, y, be positive real numbers such that x + y + = 12 and x3y4z5 = (0.1) (600)3. Then x3 + y3 + z3 is equal to :
(a) 342
(b) 216
(c) 258
(d) 270
Answer
B
Question. The sum 3/12 + 5/12+22 + 7/12+22+32 + ….. upto 11-terms is:
(a) 7/2
(b) 11/4
(c) 11/2
(d) 60/11
Answer
C
Question. Let f :R → R be a funct ion which sat isfies ƒ(x + y) = ƒ(x) + ƒ(y), ∀ x, y ∈R. If ƒ(a) = 2 and
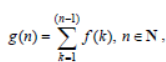
then the value of n, for which g(n) = 20, is :
(a) 5
(b) 20
(c) 4
(d) 9
Answer
A
Question. Let G be the geometric mean of two positive numbers a and b, and M be the arithmetic mean of 1/a and 1/b. If 1/M : G is 4 : 5, then a : b can be:
(a) 1 : 4
(b) 1 : 2
(c) 2 : 3
(d) 3 : 4
Answer
A
Question. For x ∈ R, let [x] denote the greatest integer ≤ x, then the sum of the series sum of the series
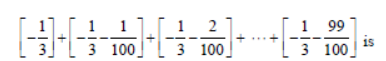
(a) –153
(b) –133
(c) –131
(d) –135
Answer
B
Question. The sum
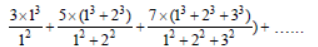
upto 10th term, is :
(a) 680
(b) 600
(c) 660
(d) 620
Answer
C
Question. If a1, a2, ………., an are in H.P., then the expression a1a2 + a2a3 + ………. + an–1an is equal to
(a) n(a1 – an )
(b) (n -1)(a1 – an )
(c) na1an
(d) (n -1)a1an
Answer
D
Question. If 1 + (1 – 22 · 1) + (1 – 42 · 3) + (1 – 62 · 5) + . . . . . . . + (1 – 202 × 19) = α – 220β, then an ordered pair (α, β) is equal to :
(a) (10, 97)
(b) (11, 103)
(c) (10, 103)
(d) (11, 97)
Answer
B
Question. The sum of the series :
(b)2 + 2(d)2 + 3(6)2 + … upto 10 terms is :
(a) 11300
(b) 11200
(c) 12100
(d) 12300
Answer
C
Question. The sum,
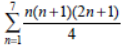
is equal to __________.
Answer
504
Question. The sum 1 + (13+23)/(1+2) + (13+23+33)/(1+2+3) + …………… + (13+23+33+….+153)/(1+2+3+….+15 )− 1/2 (1+2+3+….+15) is equal to :
(a) 620
(b) 1240
(c) 1860
(d) 660
Answer
A
Question.
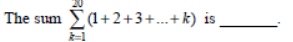
Answer
1540
Question. If m arithmetic means (A.Ms) and three geometric means (G.Ms) are inserted between 3 and 243 such that 4th A.M. is equal to 2nd G.M., then m is equal to ___________.
Answer
39
Question. If the arithmetic mean of two numbers a and b, a > b > 0, is five times their geometric mean, then a + b / a – b is equal to :
(a) √6/2
(b) 3√2/4
(c) 7√3/12
(d) 5√6/12
Answer
D
Question. If the sum of the first 40 terms of the series, 3 + 4 + 8 + 9 + 13 + 14 + 18 +19 + … is (102)m, then m is equal to:
(a) 20
(b) 25
(c) 5
(d) 10
Answer
B
Question. The sum of the series 1 + 2 × 3 + 3 × 5 + 4 × 7 + ….. upto 11th term is:
(a) 915
(b) 946
(c) 945
(d) 916
Answer
B
Question. The sum of the following series
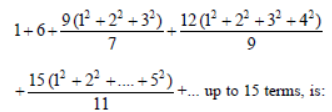
(a) 7520
(b) 7510
(c) 7830
(d) 7820
Answer
D
Question. In a geometric progression, if the ratio of the sum of first 5 terms to the sum of their reciprocals is 49, and the sum of the first and the third term is 35. Then the first term of this geometric progression is:
(a) 7
(b) 21
(c) 28
(d) 42
Answer
C
Question. The coefficient of x50 in the binomial expansion of (1 + x)1000 + x (1 + x)999 + x2(1 + x)998 + …. + x1000 is:
(a) (1000)! / (50)!(950)!
(b) (1000)! / (49)!(951)!
(c) (1000)! / (51)!(950)!
(d) (1000)! / (50)!(951)!
Answer
D
Question. The sum of the first 20 terms of the series 1 + 3/2 + 7/4 + 15/8 + 31/16 + …. is ?
(a) 38 + 1/220
(b) 39 + 1/219
(c) 39 + 1/220
(d) 38 + 1/219
Answer
D
Question. Let A be the sum of the first 20 terms and B be the sum of the first 40 terms of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 + …… If B – 2A = 100λ , then λ is equal to :
(a) 248
(b) 464
(c) 496
(d) 232
Answer
A
Question. The sum of the series 1 + 4/3 +10/9 + 28/27 + ….. upto n terms is
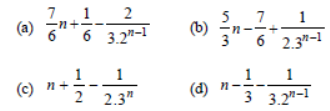
Answer
C
Question. The sum of the series 1/(1+√2) + 1/(√2+√3) + 1/(3√+√4) + …… upto 15 terms is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
C
Question. Let a, b, c ∈R. If f(x) = ax2 + bx + c is such that a + b + c = 3 and f(x + y) = f(x) + f(y) + xy, ∀ x, y ∈ R, then
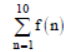
is equal to :
(a) 255
(b) 330
(c) 165
(d) 190
Answer
B
Question. If the sum of the first ten terms of the series
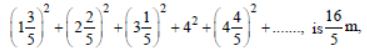
then m is equal to :
(a) 100
(b) 99
(c) 102
(d) 101
Answer
D
Question. For x ∈R, x ≠ -1, if (1 + x)2016 + x (1 + x)2015 + x2 (1 + x)2014 + …. + x2016 =
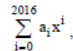
then a17 is equal to :
(a) 2017! / 17!2000!
(b) 2016! / 17! 1999!
(c) 2016! / 16!
(d) 2017! / 2000!
Answer
A
Question. The sum of the series 1 + 1/4.2! + 1/16.4! + 1/64.6! + …………… ad inf. is
(a) e-1 / √e
(b) e+1 / √e
(c) e-1 / 2√e
(d) e+1 / 2√e
Answer
D
Question. The sum of series 1/2! + 1/4! + 1/6! + …….. is
(a) (e2 – 2)/e
(b) (e – 1)2/2e
(c) (e2 – 1)/2e
(d) (e2 – 1)/2
Answer
B
Question. The sum of first 9 terms of the series. 13/1 + (13+23)/(1+3) + (13+23+33)/(1+3+5) + ……
(a) 142
(b) 192
(c) 71
(d) 96
Answer
D
Question. If
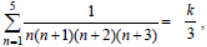
then k is equal to
(a) 1/6
(b) 17/105
(c) 55/336
(d) 19/112
Answer
C
Question. The number of terms in an A.P. is even; the sum of the odd terms in it is 24 and that the even terms is 30. If the last term exceeds the first term by 10(1/2), then the number of terms in the A.P. is:
(a) 4
(b) 8
(c) 12
(d) 16
Answer
B
Question. If the sum 3/12 + 5/12+22 + 7/12+22+32 + …… + up to 20 terms is equal to k/21, then k is equal to:
(a) 120
(b) 180
(c) 240
(d) 60
Answer
A
Question. If
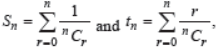
then tn/Sn is equal to
(a) (2n–1)/2
(b) 1/2(n–1)
(c) n–1
(d) (1/2)n
Answer
D
Question. The sum of the series 1/1.2 − 1/2.3 + 1/3.4 …………… up to ∞ is equal to

Answer
A
Question. The sum of first 20 terms of the sequence 0.7, 0.77, 0.777,….., is
(a) 7/81 (179 − 10−20)
(b) 7/99 (99 − 10−20)
(c) 7/81 (179 − 10−20)
(d) 7/9 (99 − 10−20)
Answer
C
Question. The value of l2 + 32 + 52 + …………………..+ 252 is :
(a) 2925
(b) 1469
(c) 1728
(d) 1456
Answer
A
Question. The sum of the series :
1 + 1/1+2 + 1/1+2+3 + ……. upto 10 terms, is :
(a) 18/11
(b) 22/13
(c) 20/11
(d) 16/9
Answer
C
Question. If

where a, b, c are in A.P and |a | < 1, | b | < 1, | c | < 1 then x, y, z are in
(a) G. P.
(b) A.P.
(c) Arithmetic – Geometric Progression
(d) H.P.
Answer
D
Question. If the sum of the roots of the quadratic equation ax2 + bx + c = 0 is equal to the sum of the squares of their reciprocals, then a/c , b/a and c/b are in
(a) Arithmetic – Geometric Progression
(b) Arithmetic Progression
(c) Geometric Progression
(d) Harmonic Progression.
Answer
D
Question.Statement-1: The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + …. + (361 + 380 + 400) is 8000.
Statement-2:
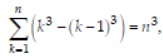
for any natural number n.
(a) Statement-1 is false, Statement-2 is true.
(b) Statement-1 is true, statement-2 is true; statement-2 is a correct explanation for Statement-1.
(c) Statement-1 is true, statement-2 is true; statement-2 is not a correct explanation for Statement-1.
(d) Statement-1 is true, statement-2 is false.
Answer
B
Question. If the sum of the series 12 + 2.22 + 32 + 2.42 + 52 + … 2.62 +… upto n terms, when n is even, is n(n+1)2 / 2 , then the sum of the series, when n is odd, is
(a) n2(n + 1)
(b) n2(n − 1)/2
(c) n2(n + 1)/2
(d) n2(n − 1)
Answer
C
Question. The sum of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 + …. + 2(2m)2 is
(a) m(2m + 1)2
(b) m2(m + 2)
(c) m2(2m + 1)
(d) m(m + 2)2
Answer
A
Question. 13 – 23 + 33 – 43 + … + 93 =
(a) 425
(b) –425
(c) 475
(d) –475
Answer
A
Question. The value of 21/4 . 41/8 . 81/16 … ∞ is
(a) 1
(b) 2
(c) 3/2
(d) 4
Answer
B
Question. The sum to infinite term of the series 1 + 2/3 + 6/32 + 10/33 + 14/34 … is
(a) 3
(b) 4
(c) 6
(d) 2
Answer
A
Question. The sum of series 1/2! − 1/3! + 1/4! − ……….. upto infinity is
(a) e½
(b) e+½
(c) e-2
(d) e-1
Answer
D
Question. The sum of the first n terms of the series 12 + 2.22 + 32 + 2.42 + 52 + 2.62 + …. is n(n+1)2 / 2 when n is even. When n is odd the sum is
(a) [ n(n+1) / 2 ]2
(b) n2(n+1) / 2
(c) n(n+1)2 / 4
(d) 3n(n+1) / 2
Answer
B
Question. The value of
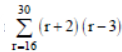
is equal to :
(a) 7770
(b) 7785
(c) 7775
(d) 7780
Answer
D
Question. If (10)9 + 2(11)1(108) + 3(11)2(10)7 +….. +10(11)9 = K(10)9, then k is equal to:
(a) 100
(b) 110
(c) 121/10
(d) 441/100
Answer
A
Question.
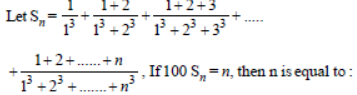
(a) 199
(b) 99
(c) 200
(d) 19
Answer
A
Question. If the sum of the first n terms of the series √3 + √75 + √243 + v507 +…… is 435√3 , then n equals :
(a) 18
(b) 15
(c) 13
(d) 29
Answer
B
Question. Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation
(a) x2 -18x -16 = 0
(b) x2 -18x +16 = 0
(c) x2 +18x -16 =0
(d) x2 +18x +16 = 0
Answer
B
Question. Sum of infinite number of terms of GP is 20 and sum of their square is 100. The common ratio of GP is
(a) 5
(b) 3/5
(c) 8/5
(d) 1/5
Answer
B
Question. If b2, a2, c2 are in A.P., then 1/a + b, 1/b + c, 1/c + a will be in
(a) A.P.
(b) G.P.
(c) H.P.
(d) None of these
Answer
A
Question. If p, q, r are in A.P., a is G.M. between p & q and b is G.M. between q and r, then a2, q2, b2 are in
(a) G.P.
(b) A.P.
(c) H.P
(d) None of these
Answer
B
Question. Sum of the first n terms of the series 1/2 + 3/4 + 7/8 + 15/16 + ……… is equal to :
(a) 2n – n – 1
(b) 1 – 2–n
(c) n + 2–n – 1
(d) 2n + 1
Answer
C
Question. If 1/b–a + 1/b–c = 1/a + 1/c then a, b, c are in
(a) A.P.
(b) G.P.
(c) H.P.
(d) In G.P. and H.P. both
Answer
C
Question. An infinite G.P has first term x and sum 5, then
(a) x < – 10
(b) – 10 < x < 0
(c) 0 < x < 10
(d) x > 10 C
(d) 4 : 1
Answer
A
Question. If Sn denotes the sum of n terms of a G.P. whose first term is a and the common ratio r, then value of S1 + S3 + S5+ …..+S2n–1 is
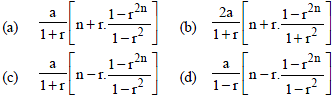
Answer
D
Question. Three numbers form an increasing G.P. If the middle number is doubled, then the new numbers are in A.P. The common ratio of the G.P. is:
(a) 2 – √3
(b) 2 + √3
(c) √3 – 2
(d) 3+ √2
Answer
B
Question. The harmonic mean of a/1–ab and a/1+ab is :
(a) a
(b) a/1–a2b2
(c) 1/1–a2b2
(d) a/1+a2b2
Answer
A
Question. If a, b, c, d, e, f are in A.P., then e – c is equal to:
(a) 2(c – a)
(b) 2(d – c)
(c) 2(f – d)
(d) (d – c)
Answer
B
Question. Let Sn denote the sum of first n terms of an A.P. If S2n = 3 Sn, then the ratio S3n/ Sn is equal to :
(a) 4
(b) 6
(c) 8
(d) 10
Answer
B
Question. Let Tr be the rth term of an A.P. whose first term is a and common difference is d. If for some positive integers m,n, m ≠ n, Tm = 1/n and Tn = 1/m, then a – d equals
(a) 1/m + 1/n
(b) 1
(c) 1/mn
(d) 0
Answer
D
Question. If the ratio of H.M. and G.M. between two numbers a and b is 4 : 5, then the ratio of the two numbers will be
(a) 1 : 2
(b) 2 : 1
(c) 4 : 1
(d) 1 : 4
Answer
C
Question. Third term of the sequence whose nth term is an = 2n, is
(a) 2
(b) 4
(c) 8
(d) 3
Answer
C