Worksheets For Class 10 Mathematics Trigonometry

Trigonometry Class 10 Worksheet have been designed as per the latest pattern for CBSE, NCERT and KVS for Grade 10. Students are always suggested to solve printable worksheets for Mathematics Trigonometry Grade 10 as they can be really helpful to clear their concepts and improve problem solving skills. We at worksheetsbag.com have provided here free PDF worksheets for students in standard 10 so that you can easily take print of these test sheets and use them daily for practice. All worksheets are easy to download and have been designed by teachers of Class 10 for benefit of students and is available for free download.

Mathematics Trigonometry Worksheets for Class 10

We have provided chapter-wise worksheets for class 10 Mathematics Trigonometry which the students can download in Pdf format for free. This is the best collection of Mathematics rigonometry standard 10th worksheets with important questions and answers for each grade 10th Mathematics rigonometry chapter so that the students are able to properly practice and gain more marks in Class 10 Mathematics Trigonometry class tests and exams.

Chapter-wise Class 10 Mathematics Trigonometry Worksheets Pdf Download

Question. If cosα /cosβ = mand  cosα /sinβ =n,(m² + n²)cos2β =?   
A) 2 m
B) 2 n
C) (m + n)
D) (m – n)

Question. If 7cosecΦ -3cotΦ = 7, then 7cotΦ – 3cosecΦ?   
A) 1
B) 2
C) 3
D) 4

Question. The value of 2(sin6Φ + cos6Φ) -3(sin4Φ + cos4Φ) = ?   
A) 0
B) 1
C) 2
D) 3

Question. If tan = 5/6 θ+Φ = 90 the value of cotΦ ?   
A) 1/6
B) 3/6
C) 5/6
D) 7/6

Question. If A,B are acute angle and sinA=cosB, then the value of A+B=?   
A) 300
B) 600
C) 900
D) 700

Question. If tan5Φ =1, then Φ ?   
A) 80
B) 70
C) 60
D) 90

Question. If sinΦ/1+cosΦ + 1+cosΦ /sinΦ = 4, Then Φ = ?   
A) 10⁰
B) 20⁰
C) 30⁰
D) 0

Question. The value of tanΦ in terms of sinΦ =?   
A) sinΦ /√(1+sin²Φ )
B) sin2Φ /1-sinΦ
C) sin2Φ /1+sinΦ
D) sinΦ /√(1+sin²Φ )

Question. If secΦ + tanΦ = 4sinΦ &cosΦ = ?   
A) 2/17 , 3/17
B) 15/17 , 8/17
C) 5/6
D) 7/6

VERY SHORT ANSWER TYPE QUESTIONS

Question. If cosec θ = 15/7 and θ + α = 90° , find the value of sec θ.

Question. If A, B and C are the angles of a triangle, then find the value of cot (B + C)/2 in terms of A.

Question. What is the value cos 1° cos 2° cos 3° …. cos 89° cos 90° …… cos 180°?

Question. If 7 sin² θ + 3 cos²θ = 4, find the value of tan θ if 0° ≤ θ ≤  90°.

Question. Find the value of cosθ – cos³θ/sinθ – sin³θ .

Question. If tanA = 1/√3 and sinB = 1/√2 , find the value of A + B.

Question. Write the value of sin2 68° + sin² 22° – 1.

Question. If cos 3θ = 1, then find the value of tan θ.

Question. If A and B are acute angles and sin B = cos A, then write the value of A + B.

Question. Write the value of sin (55° + θ) – cos (35° – θ).

Question. Express tan 87° + sin 63° in terms of trigonometric ratios of angles between 0° and 45°.

Question. Write the value of tan 5° tan 35° tan 45° tan 55° tan 85°.

Question. If tan (θ – 36°) = cot 2θ; 2θ and (θ – 36°) are acute angles, then find θ.

Question. If tan² θ – 5 tan θ + 1 = 0, find the value of tanθ + cot θ.

Question. Write the simplest form of sinθ/sec(90° – θ) + cosθ/cosec (90° – θ)

Question. What is the maximum value of 1/cosec θ ?

Question. If sin 2θ = √3/2 , find the value of cos θ .

Question. If sin θ+ cosθ = 1, the find the value of sin θ cos θ.

Question. If cosec²θ (1 + cos θ) (1 – cos θ) = k, then find the value of k.

Question. If sin 2θ = cos 3θ, then find the value of θ.

CBSE Class 10 Mathematics Trigonometry Worksheet Set A

CBSE Class 10 Mathematics Trigonometry Worksheet Set B

CBSE Class 10 Mathematics Trigonometry Worksheet Set C

CBSE Class 10 Mathematics Trigonometry Worksheet Set D

CBSE Class 10 Mathematics Trigonometry Worksheet Set E

CBSE Class 10 Mathematics Trigonometry Worksheet Set F

CBSE Class 10 Mathematics Trigonometry Worksheet Set G

CBSE Class 10 Mathematics Trigonometry Worksheet Set H

CBSE Class 10 Mathematics Trigonometry Worksheet Set I

CBSE Class 10 Mathematics Trigonometry Worksheet Set J

CBSE Class 10 Mathematics Trigonometry Worksheet Set K

CBSE Class 10 Mathematics Trigonometry Worksheet Set L

CBSE Class 10 Mathematics Trigonometry Worksheet Set M

CBSE Class 10 Mathematics Trigonometry Worksheet Set N

CBSE Class 10 Mathematics Trigonometry Worksheet Set O

CBSE Class 10 Mathematics Trigonometry Worksheet Set P

CBSE Class 10 Mathematics Trigonometry Worksheet Set Q1

CBSE Class 10 Mathematics Trigonometry Worksheet Set Q2

CBSE Class 10 Mathematics Trigonometry Worksheet Set Q4

CBSE Class 10 Mathematics Trigonometry Worksheet Set Q5

CBSE Class 10 Mathematics Trigonometry Worksheet Set Q6

CBSE Class 10 Mathematics Trigonometry Worksheet Set S1

CBSE Class 10 Mathematics Trigonometry Worksheet Set S2

CBSE Class 10 Mathematics Trigonometry Worksheet Set U

CBSE Class 10 Mathematics Trigonometry Worksheet Set V

CBSE Class 10 Mathematics Trigonometry Worksheet Set W

CBSE Class 10 Mathematics Trigonometry Worksheet Set X

CBSE Class 10 Mathematics Trigonometry Worksheet Set Y

CBSE Class 10 Mathematics Trigonometry Worksheet Set Z

PRACTICE EXERCISE

Question. ABCD is a rectangle with AD =12 cm and DC = 20 cm as shown. The line segment DE is drawn making an angle of 30° with AD, intersecting AB in E. Find the lengths of DE and AE.

Solution. DE = 8 √3 cm, AE = 4 √3 cm

Question. Evaluate each of the following :   

Solution. (i) 1 (ii) 2 (iii) 2 (iv) 0

Question. Evaluate each of the following :
(i) tan 5° tan 25° tan 30° tan 45° tan 65° tan 85° (ii) cot 12° cot 38° cot 52° cot 60° cot 78°
(iii) sec (35° + A) – cosec (55° – A) (iv) cos (36° + A) – sin (54° – A)
Solution. (i) 1/√3 (ii) 1/√3 (iii) 0 (iv) 0

Question. Evaluate each of the following :
(i) sin 54° – cos 36° (ii) tan 62° – cot 28°
(iii) cosec 47° – sec 43° (iv) sec² 31° – cot² 59°
(v) sin² 29° + sin² 61 (vi) tan² 48° – cosec²42°
Solution. (i) 0 (ii) 0 (iii) 0 (iv) 1 (v) 1 (vi) –1

Question. If 21 cosec θ = 29, find the value of : 
(i) cos² θ – sin ²θ/1 – 2sin² θ    (ii) 2cos² θ – 1/cos² θ – sin² θ 
Solution. (i) 1 (ii) 1

Question. If sin A – 1/sin A = 3 , find the value of sin2 A + 1/sin² A.
Solution. 11

Question. Evaluate each of the following :   

Solution. (i) 1 (ii) 0 (iii) √3 + 4/2 (iv) 3/4 (v) 6 (vi) 5/6 (2 -√3) (vii) 6 (viii) 9

Question. Given that sin (A + B) = sin A cos B + cos A sin B, find the value of sin 75°.
Solution. √3 + 1/2√2

Question. Given that cos (A – B) = cos A cos B + sin A sin B, find the value of cos 15°.
Solution. √3 + 1/2√2

Question. Find x in each of the following, if :
(i) 2 cos x = 1 (ii) 2 sin 2x = 1 (iii) tan 3x =√3 (iv) 2sin 3x =√3  (v) √3 cot 3x = 1  (vi) √3.sec(x/) = 2
Solution. (i) 60° (ii) 15° (iii) 20° (iv) 20° (v) 20° (vi) 60°

Question. Find acute angle θ in each of the following cases; if,
(i) sin (3θ – 15°) = 1 (ii) 2 sin (3θ – 15°) √3  (iii) sin2 θ = 1/4  (iv) 3tan2 θ – 1 = 0 (v) cos (40° + θ) = sin 30°  (vi) cot2 (2θ – 5°) = 3
Solution. (i) 35° (ii) 25° (iii) 30° (iv) 30° (v) 20° (vi) 17.5°

Question. If sin (A 2B) = √3/2 and cos (A + 4B) = 0, find the values of angles A and B.
Solution. A = 30°, B = 15°

Question. If sin (A + B) = 1 and cos (A B) = √3/2 ; 0° <A + B ≤ 90° , and A > B, find A and B.
Solution. A = 60°, B = 30°

Question. ABC is a right triangle, right angled at C. If A = 30°, and AB = 40 units, find the remaining two sides and ∠B of ΔABC. 
Solution. AC = 20 √3 units, BC = 20 units and B = 60°

Question. If sin (A – B) 1/2 and cos (A + B) = 1/2 ; 0° <A + B < 90° , and A > B, find A and B.
Solution. A = 45°, B = 15°

Question. If tan θ = a/b , find the value of cos θ + sin θ/cos θ – sin θ .
Solution. b + a/ b – a 

Question. In ΔABC, right angled at B, AC + BC = 25 cm and AB = 5 cm, find the value of sin2A + cos2A.
Solution. 1

Question. Evaluate each of the following : 

Solution. (i) 2 (ii) 0 (iii) 2 (iv) 0

Question. Without using trigonometric tables, find the value of each of the following : 

Solution. (i) 1 (ii) 1 (iii) 1 (iv) 2 (v) √3 (vi) -3 /4 (vii) 2 (viii) – 5/ 12 (ix) 1+ 2 √3 (x) 0

Question. In ΔABC, right angled at B, if AB = 12 cm and BC = 5 cm, find (i) sin A and tan A (ii) sin C and cot C.
Solution. (i) 5/13 , 5/12 (ii) 12/13 , 5/12

Question. In each of the following, one of the six trigonometric ratios is given. Find the values of the other trigonometric ratios.
(i) sinθ = 15/17 (ii) cotθ = 3/4 (iii) cosθ = 7/25 (iv) secθ = 13/5 (v) cosecθ = 41/9 (vi) tanθ = 5/12
Solution.  

Question. If sec 5 θ = cosec (θ – 36°), where 5θ is an acute angle, find the value of θ.
Solution. 21°

Question. Using trigonometric identities, write the following expressions as an integer :
(i) 5 cot² A – 5 cosec² A (ii) 4 tan2 θ – 4 sec² θ
(iii) 7 cos²θ + 7 sin²θ (iv) 3 sec²α – 3 tan²α
Solution. (i) –5 (ii) –4 (iii) 7 (iv) 3

Question. Simplify the following expressions :   

Solution. (i) sin θ (ii) 1 – sin θ cos θ (iii) 2 sec2 A (iv) 1 (v) tan² α (vi) 1

Question. If 2 tan θ = 1, find the value of 3cos θ + 2sinθ/2cos θ – sin θ .
Solution. 8/3

Question. Express each of the following in terms of trigonometric ratios of angles between 0° and 45° :
(i) sin 79° + cosec 83° (ii) tan 58° + sec 46°
(iii) cosec 57° + cot 57° (iv) sin 82° + tan 82°
Solution. (i) cos 11° + sec 9° (ii) cot 32° + cosec 44° (iii) sec 33° + tan 33° (iv) cos 8° + cot 8°

Question. If sin 3θ = cos (θ – 6°), where 3θ and θ – 6°) are acute angles, find the value of θ.
Solution. 24°

Question. If cot θ =13/12 , find the value of 2sin θ cos θ/cos2 θ – sin² θ .
Solution. 312/25

Question. If tan²θ = cot (θ + 6°), where 2θ and θ + 6° are acute angles, find the value of θ.
Solution. 28°

Question. Prove that: 2 sec ² θ – sec ⁴ θ – 2 cosec ² θ + cosec ⁴ θ = cot ⁴ θ -tan⁴ θ.
Sol. LHS = 2 sec ² θ – sec ⁴ θ – 2 cosec ² θ + cosec ⁴ θ
             = 2 (sec ² θ) – (sec ² θ)2 – 2 (cosec ² θ) + (cosec 2 θ)2
             = 2 (1 + tan2 θ) – (1 + tan² θ)2 – 2 (1 + cot ² θ) + (1 + cot ² θ)2
             = 2 + 2 tan² θ – (1 + 2 tan² θ + tan⁴ θ) – 2 – 2 cot ² θ + (1 + 2 cot ² θ + cot ⁴ θ)
             = 2 + 2 tan² θ -1 – 2 tan² θ – tan⁴ θ – 2 – 2 cot ² θ +1 + 2 cot ² θ + cot 4 θ
             = cot ⁴ θ – tan⁴ θ = RHS.

Question. Prove that: cotθ – tanθ = 2cos²θ – 1/sinθ cosθ
Sol.

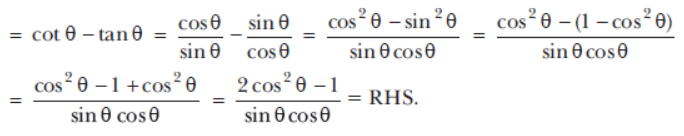
Question. Prove that: (1 – sin A + cos A)² = 2 (1 -sin A)(1 + cos A).
Sol. LHS = (1 – sin A + cos A)²
             = 1 + sin² A + cos² A – 2 sin A + 2 cos A – 2 sin A cos A
             = 1 +1 – 2 sin A + 2 cos A – 2 sin A cos A [Q sin² A + cos² A = 1 ]
             = 2 (1 – sin A + cos A – sin A cos A) = 2 [(1 – sin A) + cos A (1 – sin A)]
             = 2 (1 – sin A) (1 + cos A) = RHS.

Question.. Prove that: 1/(cosec x +cot x) – 1/sin x= 1/sin x- 1(cosec x cot x)
Sol. In order to show that,
                  1/(cosec x +cot x) – 1/sin x= 1/sin x- 1(cosec x cot x)
It is sufficient to show
                  1/(cosec x +cot x)+1(cosec x cot x)= 1/sin x+1/sin x
                  1/(cosec x +cot x)+1(cosec x cot x)= 2/sin x                     …..(i)
Now, LHS of above is

Question. Prove that: (cosec A – sin ) (secA – cosA ) = 1/(tanA + cotA)
Sol. LHS = (cosec A – sin A) (sec A – cos A)

Question. If x sin³θ + y cos³θ = sinθ cosθ and xsinθ = ycos θ, prove x² + y² =1.
Sol. We have,
x sin³ θ + y cos³ θ = sin θ cos θ
⇒ ( sin x θ) sin² θ + (y cos θ) cos² θ = sin θ cos θ
⇒ x sin θ (sin² θ) + (x sin θ) cos² θ = sin θ cos θ          [∴ x sin θ = y cos θ]
⇒ x sin θ (sin² θ + cos² θ) = sin θ cos θ
⇒ x sin θ = sin θ cos θ ⇒ x = cos θ
Now, we have x sin θ = y cos θ
⇒ cos q sin θ = y cos θ                                                [∴ x = cos θ]
⇒              θ = sin θ
Hence, x ² + y² = cos² θ + sin² θ =1.

Question. If cosec θ – sin θ = l and sec θ – cos θ = m, prove that l 2m² (l ²+m²+ 3)= 1.
Sol. LHS, = l ²m² (l ² + m² + 3)
= (cosec θ – sin θ)² (sec θ – cos θ)² { (cosec θ – sin θ)² + (sec θ – cos θ)² + 3 }

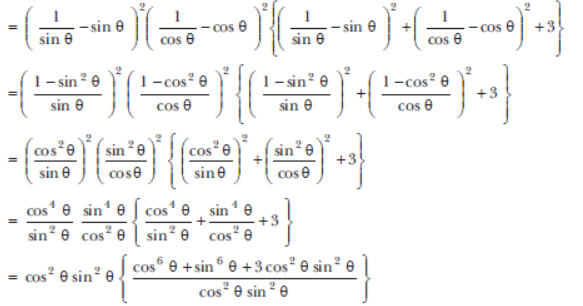
= cos⁶ θ + sin⁶ θ + 3 cos²θ sin² θ
= [(cos² θ)3 + (sin² θ)3] + 3 cos² θ sin² θ
= [(cos² θ + sin² θ)3 – 3 cos² θ sin² θ (cos² θ + sin2 θ)] + 3 cos² θ sin² θ
[∴ a³ + b³ = (a + b)³ – 3ab (a + b)]
= 1 – 3 cos² θ sin² θ + 3 cos² θ sin² θ [∴ cos² θ + sin2 θ =1]
= 1 = RHS.

Question. Prove that: ( sin θ + sec θ )² +(cos θ + cosec θ)² =(1 + sec θ cosec θ )².
Sol. LHS = (sin θ + sec θ)² + (cos θ + cosec θ)²

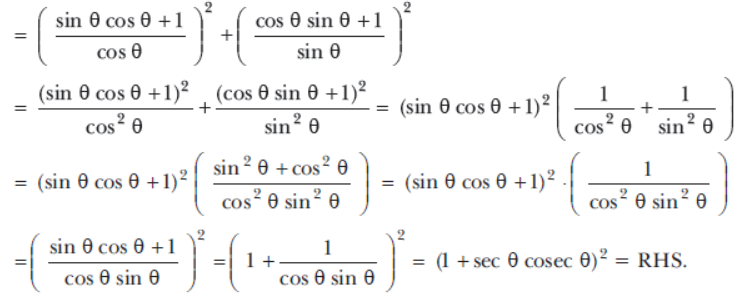
Question. If tanθ + sinθ = m and tan θ – sin θ = n, show that (m² – n² ) = 4 mn.
Sol. We have given tanθ + sinθ = m, and tanθ- sinθ = n, then
LHS = (m² – n²) = (tan θ + sin θ)² – (tan θ – sin θ)²
       = tan² θ + sin² θ + 2 tan θ sin θ – tan² θ – sin² θ + 2 tan θ sin θ

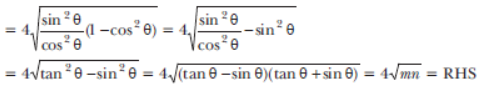
Question. If tan A = n tan B and sin A = m sin B, prove that cos²A(m²-1)/(n²-1)
Sol. We have to find cos² A in terms of m and n. This means that the angle B is to be eliminated from the given relations.
Now, tan A = n tan B    ⇒     tan B tan=1/n tanA  ⇒   cotB=n/tanA
and   sin A = m sin B    ⇒     sin B  sin=1/m sin A  ⇒  cosecB=1/sinA
Substituting the values of cot B and cosec B in cosec² B – cot ² B =1, we get

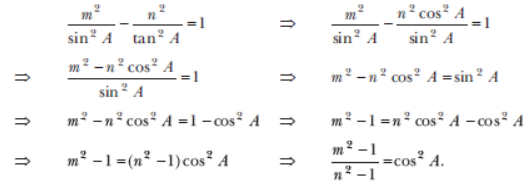
Question. Prove that: (sin A + cosec A)² + (cos A + sec A)² = 7 + tan2 A + cot ² A. 
Sol. LHS = (sin A + cosec A)² + (cos A + sec A)²
= sin2 A + cosec ² A + 2 sin A . cosec A + cos² A + sec ² A + 2 cos A . sec A
= (sin² A + cosec ² A + 2) + (cos² A + sec ² A + 2)                                     {sinA . cosecA = 1}
                                                                                                                    {cosA . secA = 1}
= (sin² A + cos² A) + (cosec ²A + sec ² A) + 4
=1 +1 + cot ² A +1 + tan² A + 4
= 7 + tan² A + cot ² A = RHS.

Question. Prove the following identity, where the angle involved is acute angle for which the expressions are defined.

Question. Prove that: (cosecθ – cotθ )²= 1-cosθ/1+cosθ
Sol. LHS = (cosecθ – cotθ)²

Question. Prove that:  cosecθ+cotθ/cosecθ-cotθ=(cosecθ+cotθ)2=1-2cot²θ+2 sec θ cot θ.
Sol. LHS = cosecθ+cotθ/cosecθ-cotθ
Rationalising the denominator, we get

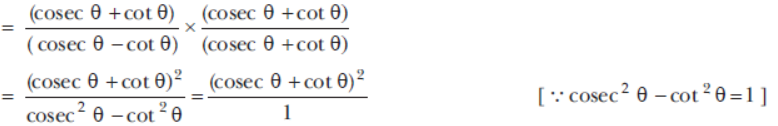
= cosec ² θ+ cot ² θ + 2 cosec θ.cot θ
= (1 + cot ² θ) + cot ² θ + 2 cosec θ. cot θ
= 1 + 2 cot ² θ + 2 cosec θ.cot θ = RHS.

Question. Two pillars are of equal height and on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillars are 60° and 30° at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.   
Solution. Let AB and CD be two pillars, each of height h meters. Let E be a point on the road such that AE
= x m. Then CE = (100 – x) m.

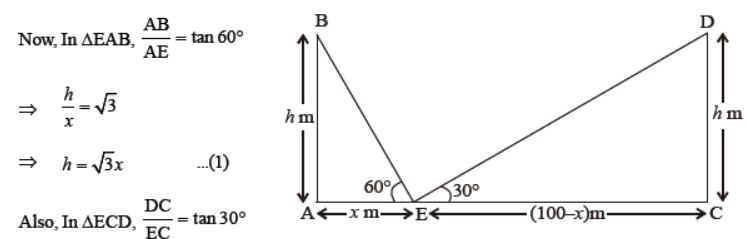
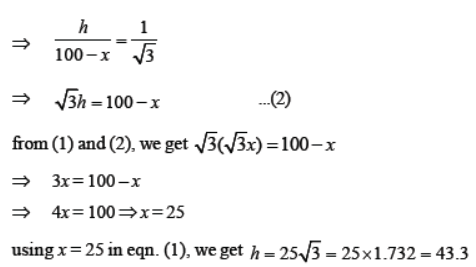
Hence, the required point is at a distance of 25 meters from the first pillar and 75 meters from the second pillar. The height of the pillars is 43.3 metres.

Question. As observed from the top of a 75 m tall light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships. 
Solution. Let AB be the light house 75 m high and C and D be the positions of two ships such that ∠XAD = 30° = ∠ADB and ∠XAC = 45° = ∠ACB 

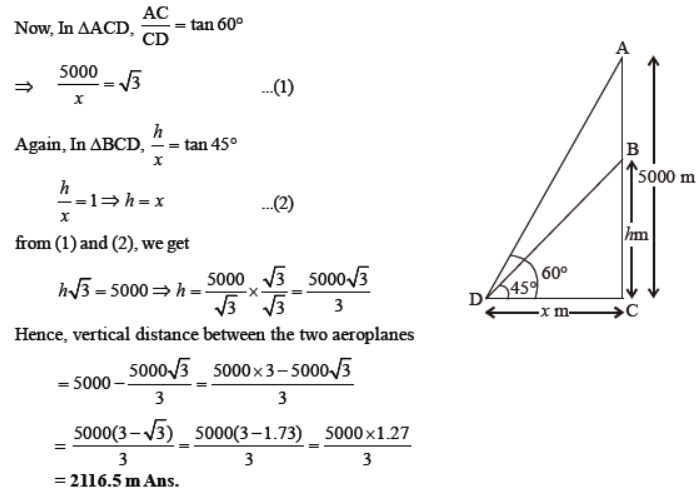
Question. An aeroplane when flying at a height of 5000 m from the ground passes vertically above another aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at the instant.   
Solution. Let the height of first aeroplane be AC and height of second aeroplane be BC = h meters.

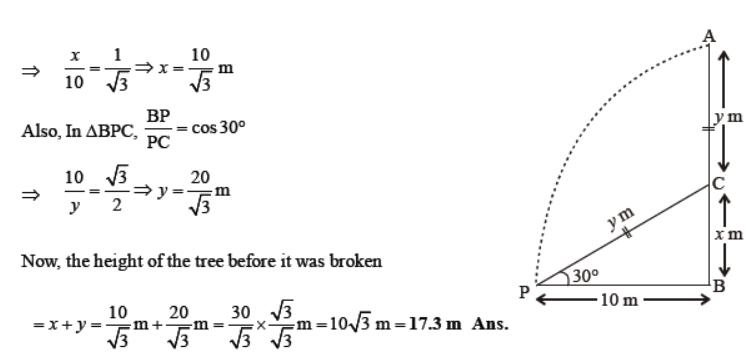
Question. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 m. Find the height of the tree before it was broken.   
Solution. Let AB was the tree in its original position and due to storm it is broken through the point C. The top of the tree, after it breaks touches the ground at point P.
Now, In ΔBPC , BC/BP = tan 30°

Question. A man standing on the deck of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill. 
Solution. Let the man is standing on the deck of a ship at a point A and let CD be the hill. Draw AE⊥CD.
Clearly, ∠EAC = ∠ACB (∴ alternate angles)
Now, In ΔAED, we have,   

Question. The angles of elevation of the top of a tower from two points at distances a and b meters from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab meters.
Solution. Let AB be the tower. Let C and D be two points at distances a and b respectively from the base of the tower. Then, AC = a, AD = b. Let ∠ACB = ∠ and ∠ADB = 90° – θ.
Let h be the height of the tower AB.     

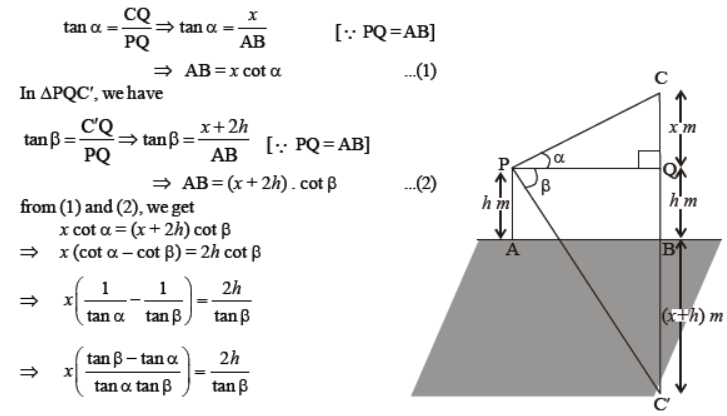
Question. If the angle of elevation of a cloud from a point h metres above a lake is α and the angle of depression of its reflection in the lake is β, prove that the height of the cloud is h(tan β +tan α)/tan β –tan α
Solution. Let AB be the surface of the lake and P be a point of observation such that AP = h metres. Let C be the position of the cloud and C’ be its reflection in the lake. Then, CB = C’B. Clearly, CB = CQ + QB = (x + h) m
Now, In ΔCPQ, we have   

Question. The shadow of a tower standing on a level ground is found to be 45 m longer when the sun’s altitude is 30° than when it was 60°. Find the height of the tower.  1
Solution. Let the height of the tower AB is h metre.
Let BD is the shadow of the tower when sun’s altitude is 30° and BC is the shadow when sun’s altitude is 60°.

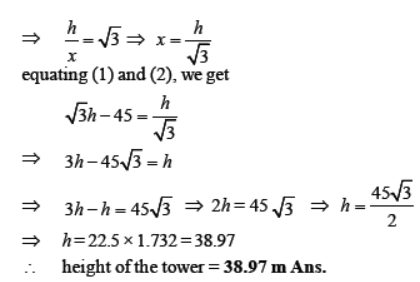
Question. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six minutes later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower. 
Solution. Let AB is a tower and D and C are respectively the positions of the car, approaching the foot of the tower with uniform speed such that
∠XAD = ∠ADB = 30°
and, ∠XAC = ∠ACB = 60° [∴ alternate angles]   

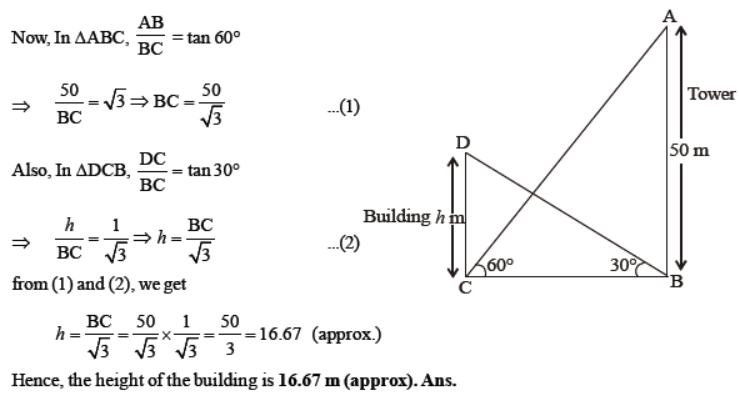
Question. The angle of elevation of the top of the building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.   
Solution. Let AB is the tower of height 50 m and CD is the building of height h m

Mathematics Trigonometry Worksheets for Class 10 as per CBSE NCERT pattern

Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 10 Mathematics Trigonometry book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Trigonometry for Class 10 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.

Benefits of Free Trigonometry Class 10 Worksheet

1. You can improve understanding of your concepts if you solve NCERT Class 10 Mathematics Trigonometry Worksheet,
2. These CBSE Class 10 Mathematics Trigonometry worksheets can help you to understand the pattern of questions expected in Mathematics Trigonometry exams.
3. All worksheets for Mathematics Trigonometry Class 10 for NCERT have been organized in a manner to allow easy download in PDF format
4. Parents will be easily able to understand the worksheets and give them to kids to solve
5. Will help you to quickly revise all chapters of Class 10 Mathematics Trigonometry textbook
6. CBSE Class 10 Mathematics Trigonometry Workbook will surely help to improve knowledge of this subject

These Printable practice worksheets are available for free download for Class 10 Mathematics Trigonometry. As the teachers have done extensive research for all topics and have then made these worksheets for you so that you can use them for your benefit and have also provided to you for each chapter in your ebook. The Chapter wise question bank and revision worksheets can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 10 Mathematics Trigonometry Worksheets PDF.