Worksheets For Class 10 Mathematics Applications Of Trigonometry

Applications of Trigonometry Worksheet Class 10 Maths have been designed as per the latest pattern for CBSE, NCERT and KVS for Grade 10. Students are always suggested to solve printable worksheets for Mathematics Applications Of Trigonometry Grade 10 as they can be really helpful to clear their concepts and improve problem solving skills. We at worksheetsbag.com have provided here free PDF worksheets for students in standard 10 so that you can easily take print of these test sheets and use them daily for practice. All worksheets are easy to download and have been designed by teachers of Class 10 for benefit of students and is available for free download.

Mathematics Applications Of Trigonometry Worksheets for Class 10

We have provided chapter-wise worksheets for class 10 Mathematics Applications Of Trigonometry which the students can download in Pdf format for free. This is the best collection of Mathematics Applications Of Trigonometry standard 10th worksheets with important questions and answers for each grade 10th Mathematics Applications Of Trigonometry chapter so that the students are able to properly practice and gain more marks in Class 10 Mathematics Applications Of Trigonometry class tests and exams.

Chapter-wise Class 10 Mathematics Applications Of Trigonometry Worksheets Pdf Download

CBSE Class 10 Applications of Trigonometry (10)_1

CBSE Class 10 Applications of Trigonometry (11)_1

CBSE Class 10 Applications of Trigonometry (12)_1

CBSE Class 10 Applications of Trigonometry (13)_1

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set A

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set B

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set C

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set E

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set G

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set I

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set K

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set L

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set M

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set N

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set O

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set P

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set Q

CBSE Class 10 Mathematics Applications Of Trigonometry Worksheet Set R

Practice Exercise :

Question. Find the angle of elevation of the sun’s altitude when the height of the shadow of a vertical pole is equal to its height:
Solution. 45°

Question. A person standing on the bank of a river observes that the angle of elevation of top of building of an organization working for conservation of wildlife. Standing on the opposite bank is 60°.When he moves 40 m away from the bank he finds the angle of elevation to be 30°.Find the height of the building and width of the river.
Solution. 20 √3, 20m

Question. A ladder 50m long just reaches the top of a vertical wall. If the ladder makes an angle of 600 with the wall, find the height of the wall.
Solution. 5(√3 + 1) m

Question. Two poles of height 6m and 11m stands vertically on the ground. If the distance between their feet is 12m. Find the distance between their tops.
Solution. 13 m

Question. An observer 1.5m tall is 20. 5 metres away from a tower 22m high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Solution. 45°

Question. From the top of a building 60m high, the angels of depression of the top and bottom of a vertical lamp post are observed to be 30° and 60°respectively. Find [i] horizontal distance between the building and the lamp post [ii] height of the lamp post.
Solution. 20 √3 , 40m

Question. The angle of depression of the top and bottom of a tower as seen from the top of a100 m high cliff are 30° and 60° respectively. Find the height of the tower.
Solution. 66.67m

Question. From a window (9m above ground) of a house in a street, the angles of elevation and depression of the top and foot of another house on the opposite side of the street are 30°and 60° respectively. Find the height of the opposite house and width of the street.
Solution. 3m ,3√3 m

Question. From the top of a hill, the angle of depression of two consecutive kilometer stones due east are found to be 30° and45°.Find the height of the hill.
Solution. 1.37km

Question. An airplane when flying at a height of 3125m from the ground passes vertically below another Plane at an instant when the angle of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
Solution. 6250m

Question. Two poles of equal heights are standing opposite each other on either side of the road, which is 80m wide. From a point between the road the angles of elevation of the top of the poles are 60° and 30°. Find the heights of pole and the distance of the point from the poles.
Solution. 20 √3 m, 20m and

Question. A vertical pole10m long casts a shadow √3 m long. At the same time tower casts a shadow 90m long. Determine the height of the tower.
Solution. 30√3 m

Question. A ladder 15m long just reaches the top of vertical wall. If the ladder makes an angle 60° with the wall, find the height of the wall.
Solution. 7.5 √3 m

Question. The angle of elevation of a jetfighter from a point A on the ground is 600.After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet is flying at a speed of 720km/hr, find the constant height at which the jet is flying.
Solution. 500 √3 m

Question. A tower is 50m high. It’s shadow is x m shorter when the sun’s altitude is 45° than when it is 30°. Find x correct to the nearest 10.
Solution. 36.6m

Question. In the adjacent figure, what are the angles of elevation and depression of the top and bottom of a pole from the top of a tower h (m) high: 8
Solution. 45°,60°

Question. A window in a building is at a height of 10 m above the ground. The angle of depression of a point P on the ground from the window is 30°.The angle of elevation of the top of the building from the point P is 60°. Find the height of the building.
Solution. 30m

Question. A boy, whose eye level is 1.3 m from the ground, spots a balloon moving with the wind in a horizontal line at same height from the ground. The angle of elevation of the balloon from the eyes of the boy at any instant is 600.After 2 seconds, the angle of elevation reduces to 300 if the speed of the wind at that moment is m/ then find the height of the balloon from the ground.
Solution. 87m

Question. A pole 3m high casts a shadow √3 m long on the ground, then find the sun’s elevation?
Solution. 60°

Question. The length of the shadow of a pillar is times its height. Find the angle of elevation of the source of light.
Solution. 30°

Question. A tower is 50m high. It’s shadow is x m shorter when the sun’s altitude is 45° than when it is 30°. Find x correct to the nearest 10.
Solution. 36.6m

Question. In the adjacent figure, what are the angles of elevation and depression of the top and bottom of a pole from the top of a tower h (m) high:

Solution. 45°,60°

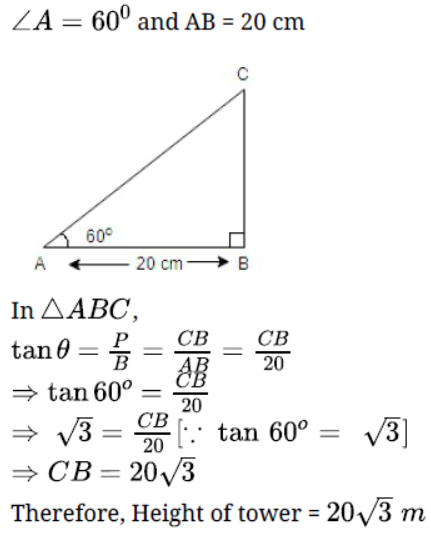
Question. In a rectangle ABCD, AB=20cm,∠BAC= 60° then find the length of the side AD.
Solution. 20 √3 m

Question. A man on the deck on a ship14m above water level observes that the angle of elevation of the top of a cliff is 600 and the angle of depression of the base of the cliff is 30°.Calculate the distance of the cliff from the ship and the height of the cliff.
Solution. 14 √3 m and 56m

Question. If length of the shadow and height of a tower are in the ratio1:1.Then find the angle of elevation.
Solution. 45°

Question. The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of the reflection of the cloud in the lake is 60°. find the height of the cloud from the surface of the lake.
Solution. 120m

Question. From a point 20 m away from the foot of a tower, the angle of elevation of top of the tower is 30°, find the height of the tower.
Solution. 20 / √3

Question. Find the angle of elevation of the sun when the shadow of a pole h m high is m long.   
Solution.

Question. A man standing on the deck of a ship which is 10 m above the water level observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30° . Calculate the distance of the hill from the ship and the height of the hill.   
Solution.

Question. A 7 m long flagstaff is fixed on the top of a tower standing on the horizontal plane. From point on the ground, the angles of elevation of the top and bottom of the flagstaff are 60o and 45o respectively. Find the height of the tower correct to one place of decimal.   
Solution.

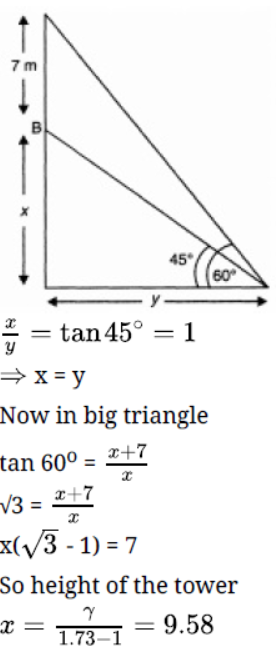
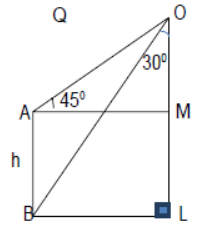
Question . A round balloon of radius r subtends an angle α at the eye of the observer while the angle of elevation of its centre is . Prove that the height of the centre of the balloon is r sin βcosec α/2 .       
Solution. Let O be the centre of the balloon of radius r and P the eye of the observer. Let PA, PB
be tangents from P to the balloon. Then, ∠APB = α

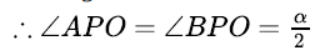
Let OL be perpendicular from O on the horizontal PX. We are given that the angle of the elevation of the centre of the balloon is i.e, ∠OPL = β

Question. The length of a string between a kite and a point on the ground is 85 m. If the string makes an angle with the ground level such that tanθ = 15/8 then find the height of the kite from the ground. Assume that there is no slack in the string.     
Solution. Let OX be the horizontal ground and let A be the position of the kite. Let O be the position of the observer and OA be the string. Draw AB⊥OX.

Question. A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from base of the tower. [Take √3 = 1.732]
Solution. Let height of tower (TR) be x m, distance (RP) of a point (P) from the base of tower be y m, height of the flagstaff (QT) be 5 m.

Question. Find the values of x and y in the following figure:
Solution. ΔABC is a right-angled triangle, in which ∠B = 90° and ∠C = 45°

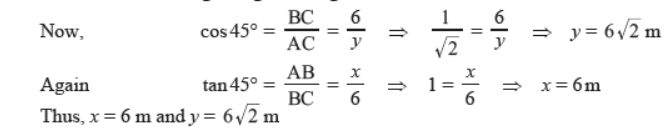
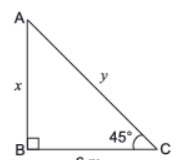
Question. The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Solution. Let AB be the tower of height 30 m and CD be another tower of height h m.

Question. The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
Solution. Let AB be the tower and angle of elevation from point C = 30°
Then, angle of elevation from point D = 30° + 15° = 45°

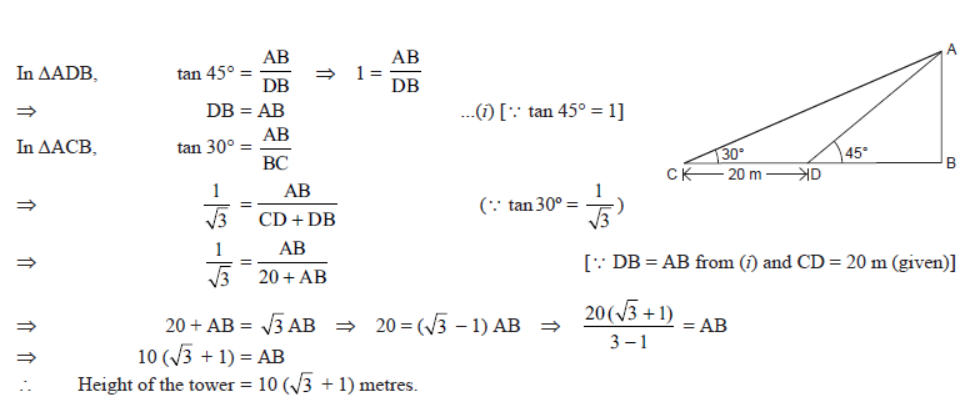
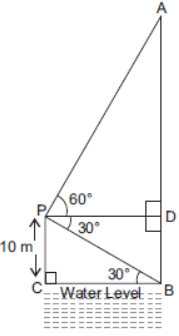
Question. A man standing on the deck of a ship, which is 10 m above the water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and height of the hill.
Solution. Let AB be the hill (A its top and B its base), P be the position of the man on the deck
C be a point on the water level and PD be the eye level of the man.
Clearly, PC = 10 m = DB
∠APD = 60° and ∠BPD = 30° = ∠PBC
We have to find AB and BC or PD.

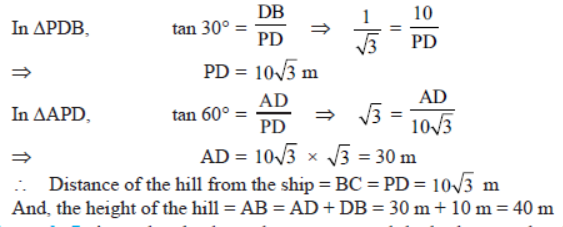
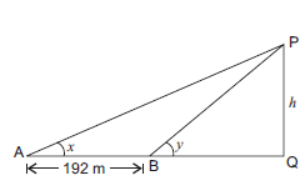
Question. At a point on level ground, the angle of the elevation of the top of a vertical tower is found to be such that its tangent is 5/12. On walking 192 metres towards the tower, the tangent of the new angle of elevation is found to be. Find the height of the tower.
Solution. Let PQ be the tower of height h metres, point A be the first point of
observation and B be the second point of observation towards the towar PQ such
that AB = 192 m.
Also, let ∠PAQ = x and ∠PBQ = y

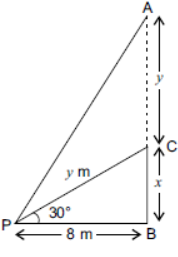
Question. A tree breaks down due to storm and the broken part bends, so that the top of the tree touches the ground making an angle of 30° with it. The distance from the foot of the tree to the point where the top touches the ground is 8 metres. Find the height of the tree before it was broken.
Solution. Let AB be the height of the tree that was broken, AC be the height of broken part of the tree and P be the point at which the top of the broken part of the tree touches.
Clearly, ∠CPB = 30° and PB = 8 m
Let CB be x m and AC = PC be y m.
Therefore, the height of the tree before it was broken = (x + y) m

Question. If cos A =5/2 , find the value of 4 + 4tan²A.   

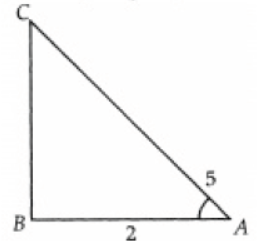
Solution.

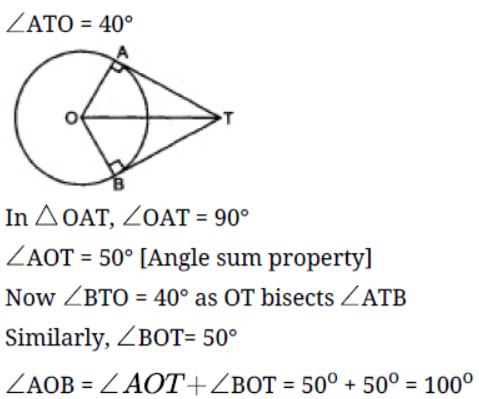
Question. In figure if ATO = 40°, find AOB.   

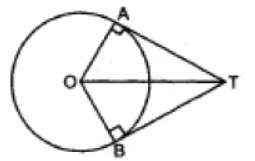
Solution. According to the question,

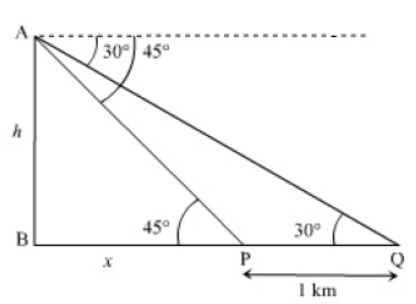
Question. The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point R, 40 m vertically above X, the angle of elevation of the top Q of tower is 45° . Find the height of the tower PQ and the distance PX. 
Solution. Let h be the height of the tower.
i.e, PQ = h m and let PX = y m
Now, draw RS ll XP ,

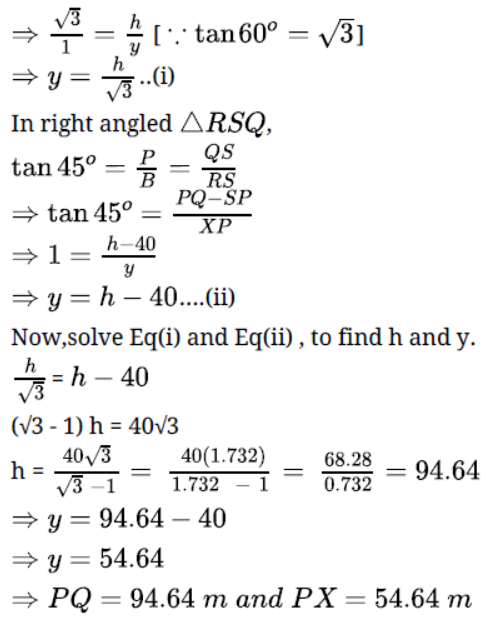
Question. The angle of depression of the top and bottom of a building 50 metres high as observed from the top of a tower are 30^o and 45^o respectively. Find the height of the tower and also the horizontal distance between the building and the tower.   
Solution.

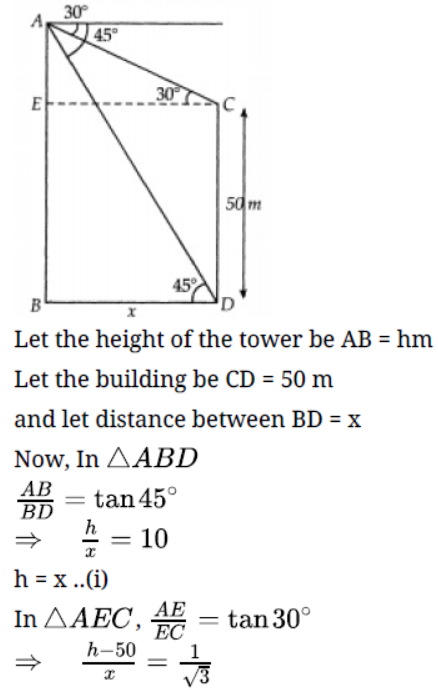
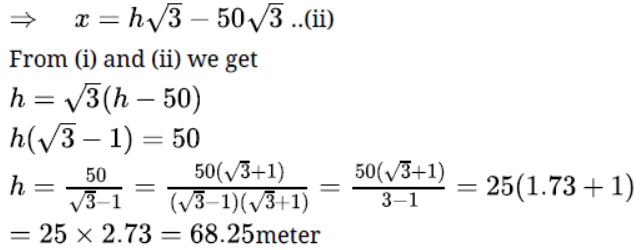
Hence the height of tower = 68.25 meter
and distance between the building and tower x= h = 68.25 meter

Question. The tops of two towers of height x and y, standing on level ground, subtend angles of 30o and 60o respectively at the centre of the line joining their feet, then find x : y.   
Solution.

Question. A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?   
Solution.

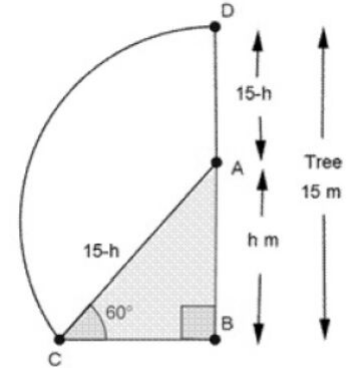
The height of the tree (DB) = 15 m
Suppose it broke at A and its top D touches the ground at C.
Suppose AB = h Then AD = AC = (15 – h) m

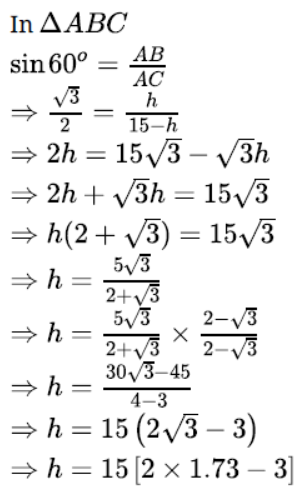
Height above the ground from where the tree broke is 6.9 meter.

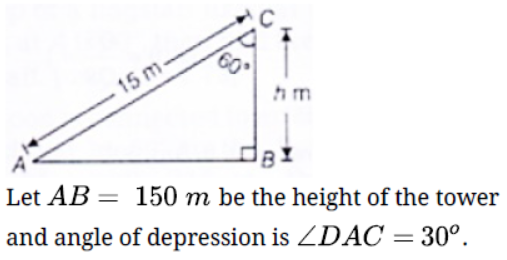
Question. The angle of depression of car parked on the road from the the top of a 150 m hightower is 30° . Find the distance of the car from the tower.   
Solution. The angle of depression of car parked on the road from the the top of a 150 m hightower is 30° .

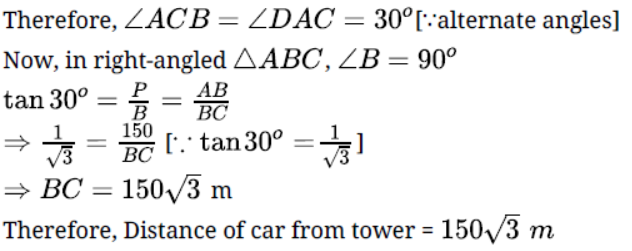
Question. A pole 6 m high casts a shadow 2√3 long on the ground, then find the Sun’s elevation.
Solution.

Question. A ladder 15 m long leans against a wall making an angle of 60o with the wall. Find the height of the wall from the point the ladder touches the wall.   
Solution. 

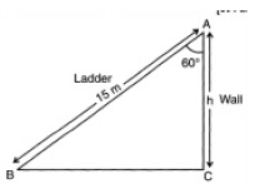
Let ABC be a right angled triangle where AB isis ladder = 15m and angle a = 60°
Let AC be the height of the wall
Therefore by Pythagoras theorem

= 7.5 m

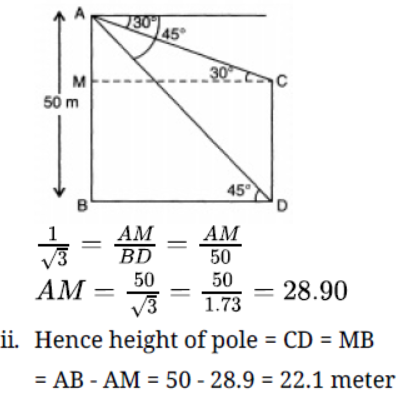
Question. A boy observes that the angle of elevation of a bird flying at a distance of 100 m is 30^o. At the same distance from the boy, a girl finds the angle of elevation of the same bird from a building 20 m high is 45o. Find the distance of the bird from the girl.   
Solution.

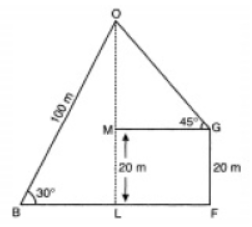
Let O be the position of the bird and B be the position of the boy. Let FG be the building and G be the position of the girl.

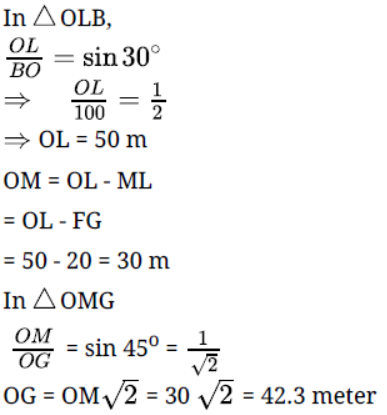
Question. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30^o.   
Solution. Let AB be the vertical pole and CA be the 20 m long rope such that its one end is tied from the top of the vertical pole AB and the other end C is tied to a point C on the ground. 

Question. From the top of a hill, the angles of depression of two consecutive kilometre stones due east are found to be 45° and 30° respectively. Find the height of the hill.   
Solution.

Given, AB is the hill and P and Q are two consecutive km stones.
Let the height of the hill AB be h m and

Question. From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30o and 45o respectively. 
Find:
i. How far the pole is from the bottom of the tower,
ii. the height of the pole.(Use √3= 1.732) 
Solution.

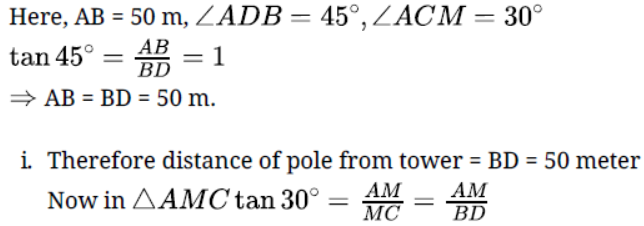
Question. A path separates two walls. A ladder leaning against one wall rests at a point on the path. It reaches a height of 90 m on the wall and makes an angle of 60° with the ground. If while resting at the same point on the path, it were made to lean against the other wall, it would have made an angle of 45° with the ground. Find the height it would have reached on the second wall.   
Solution. Let AB is path

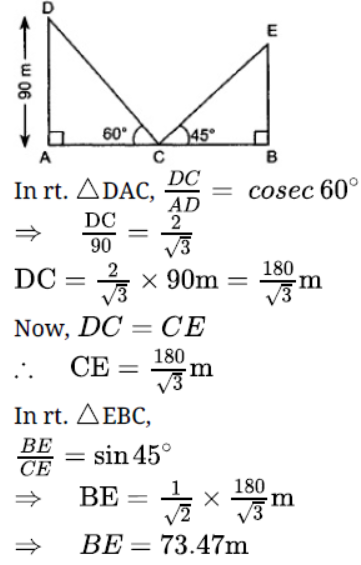
Question. If two towers of height h₁ and h₂ subtends angles of 60° and 30° respectively at the mid points of line joining their feet, find h₁ : h₂   
Solution.

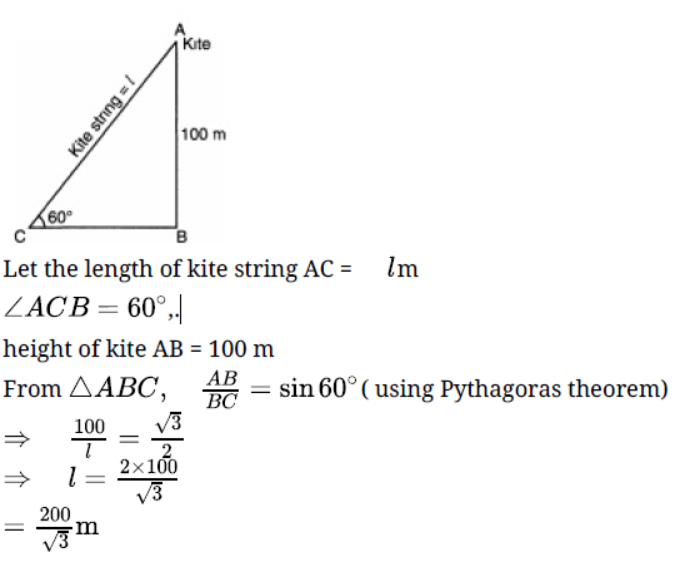
Question. Find the length of kite string flying at 100 m above the ground with the elevation of 60^o.   
Solution.

Question. If a hexagon ABCDEF circumscribe a circle, prove that AB + CD + EF = BC + DE + FA.   
Solution. Hexagon ABCDEF touches a circle at G, H, I, J, K, L. So, from the external point
tangents drawn on the circle are equal in length.
If A is external point and AG and AL are tangents, so
AG = AL …(i)
Similarly for B, BG = BH …(ii)
Similarly for C, Cl = CH … (iii)
Similarly for D, DI = DJ … (iv)
EK = EJ … (v)
and FK = FL … (vi)

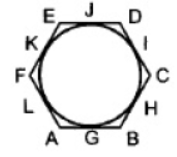
Adding (i), (ii), (iii), (iv), (v) and (vi), we get
AG + BG + CI + ID + EK + FK = BH + CH + DJ + EJ + FL + AL
⇒ (AG + BG) + (CI + ID) + (EK + FK) = (BH + CH) + (JD + EJ) + (FL + AL)
⇒ AB + CD + EF = BC + DE + FA.

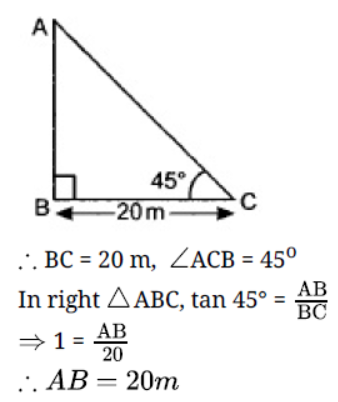
Question. The angle of elevation of the top of a tower from a point 20 metres away from the base is 45°. Find the height of the tower.   
Solution. Let AB is the tower and C is the point 20 m away from the base of the tower

Question. A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30o. Another boy is standing on the roof of a 20 m high building and is flying his kite at an elevation of 45o. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.   
Solution. Let C be the position of the first boy and AB be the building on the roof of which second boy is standing. Let the required length of the string be x m. 

Question. A bridge across a river makes an angle of 45o with the river bank as shown in Fig. If the length of the bridge across the river is 150 m, what is the width of the river? 
Solution. Given that a bridge across a river makes an angle of 45o with the river bank as shown in Fig. If the length of the bridge across the river is 150 m, we have to find the width of the river. 

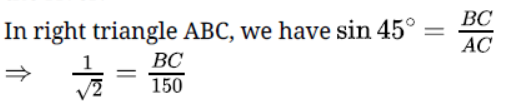
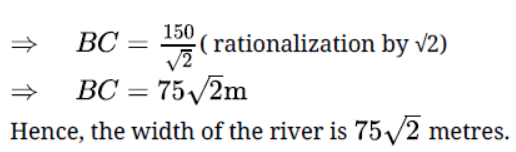
Question. An aeroplane is flying at a height of 300 m above the ground. Flying at this height the angle of depression from the aeroplane of two points on both banks of a river are 45^o and 30o respectively. Find the width of the river.   
Solution.

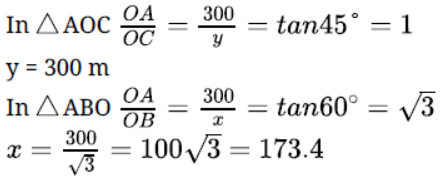
Let height of the aeroplane AO = 300 m and BO be x and OC be y.
So width of river
BC = x + y = 173.4 + 300 = 473.4 meter

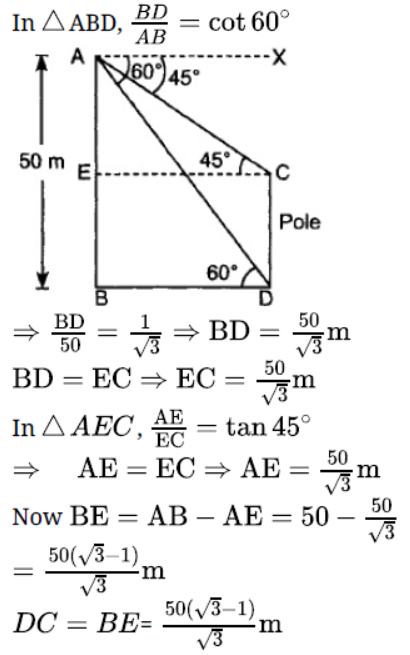
Question. Form the top of a tower 50 m high the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.   
Solution.

Question. The angle of elevation of a cloud from a point 60 m above a lake is 30° and the angle of depression of the reflection of cloud in the lake is 60°. Find the height of the cloud. 
Solution. Let AB be the surface of the lake and P be the point of observation such that AP = 60
metres. Let C be the position of the cloud and C be its reflection in the lake. Then, CB =
C’B. Let PM be perpendicular from P on CB. Then, ∠CPM = 30^o and ∠C’ PM = 60^o
Let CM = h. Then, CB = h + 60. Consequently, C’B = h + 60.
In ΔCMP , we have
Now, CB = CM + MB = h+ 60 = 60 + 60 = 120.
Hence, the height of the cloud from the surface of the lake is 120 metres.

Question. A window in a building is at height of 10 m from the ground. The angle of depression of a point P on the ground from the window is 30° .The angle of elevation of the top of the building from the point P is 60° . Find the height of the building.   
Solution. Let QS be the building and R be the position of the window in that figure.
Given, height of the window is, QR = 10m

Therefore, The height of the building would be 30 meters.

Question. Find the angle of elevation of the sun (sun’s altitude) when the length of the shadow of a vertical pole is equal to its height.   
Solution. 

According to the question,
Let height of pole (AB) = x m
Then, length of shadow (OB) = x m

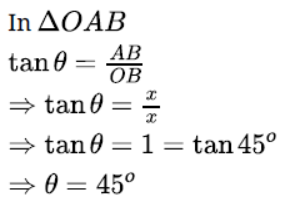
Question. In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and OTA = 30°. Find AT.   
Solution.

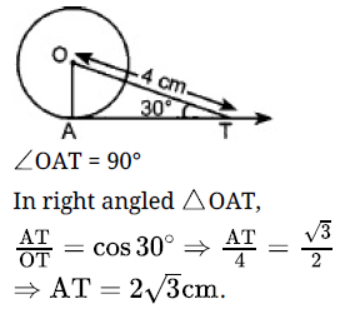
Question. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30o with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree. 
Solution.

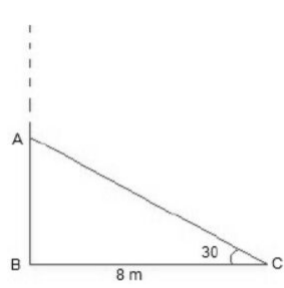
Let AC be the broken part of the tree.
∴ Total height of the tree = AB + AC

Question. A circus artist is climbing from the ground along a rope stretched from the top of a vertical pole and tied at the ground. The height of the pole is 12 m and the angle madeby the rope with ground level is 30^o. Calculate the distance covered by the artist in climbing to the top of the pole.   
Solution. Clearly, distance covered by the artist is equal to the length of the rope AC. Let AB be
the vertical pole of height 12 m. It is given that that ∠ACB = 30°
Thus, in right-angled triangle ABC, we have Perpendicular AB = 12 m,

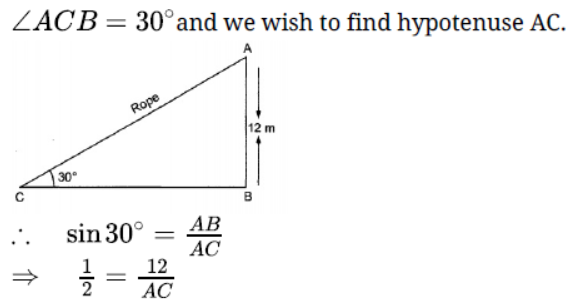
Hence, the distance covered by the circus artist is 24 m.

Question. Two ships are approaching a light house from opposite directions. The angle of depression of two ships from top of the light house are 30o and 45o. If the distance between two ships is 100 m. Find the height of light-house.   
Solution. Let AD be the height (h) of the light house and BC is the distance between two ships

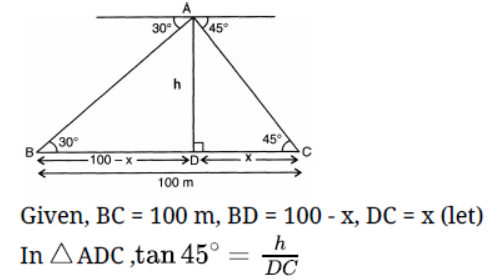
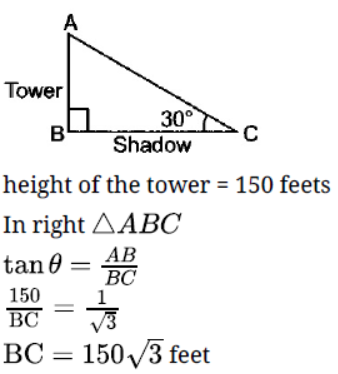
Question. If the elevation of the sun at a given time is 30°, then find the length of the shadow cast by a tower of 150 feet height at that time.   
Solution.

Question. A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30o with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.     
Solution. Let AB be the tree broken at point D, so that AD takes the position DC.

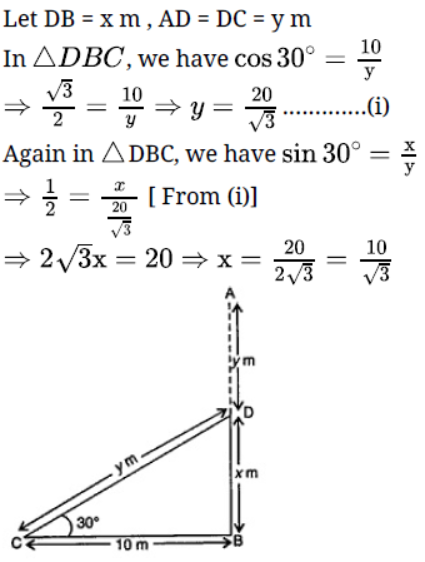
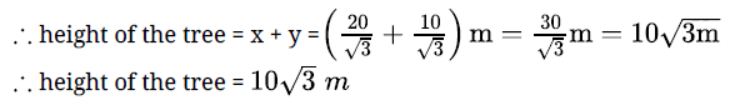
Question. A kite is flying at a height of 90 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60o. Find the length of the string assuming that there is no slack in the string.√3 = 1.32]   
Solution.

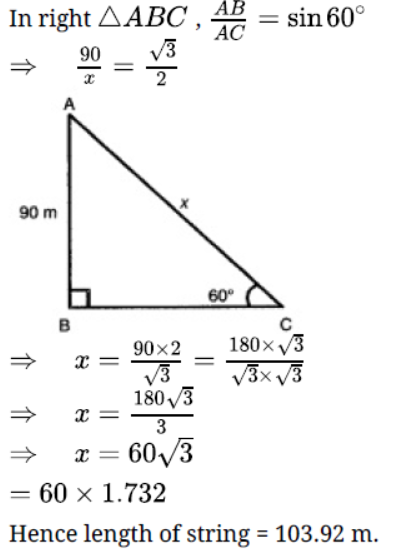
Question. The angle of elevation of an aeroplane from a point on the ground is 60° . After a flight of15 seconds, the angle of elevation changes to 30° . If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.   
Solution. Let A and B be the two positions of the aeroplane.

Question. At a point on level ground, the angle of an elevation of a vertical tower is found to be such that its tangent is 5/12 on walking 192 m towards the tower, the tangent of the angle of elevation is 3/4 . Find the height of the tower.   
Solution.

Putting the value of x in equation 1 to find the value of h(height of tower)
h = 180 m
Hence, the height of the tower = 180 m

Question. The angle of elevation of a cloud from a point 120 m above a lake is 30o and the angle of depression of its reflection in the lake is 60o. Find the height of the cloud.   
Solution.

Question. A flagstaff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flagstaff is 60o and from the same point, the angle of elevation of the top of the tower is 45o. Find the height of the flagstaff.   
Solution. Let the height of flagstaff = h m = CB
height of tower = 5 m = AB
Height of top of flagstaff from ground = (h + 5) m = AC
Let distance of point P from tower = x

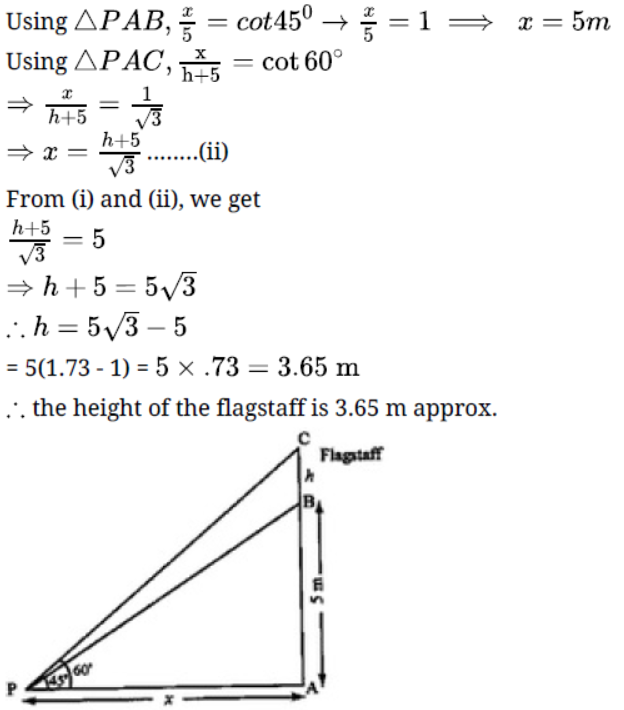
Question. The angle of elevation of a cliff from a fixed point is θ After going up a distance of k metres towards the top of the cliff at an angle of ¢ it is found that the angle of elevation is . Show that the height of the cliff is  metres. 

Solution. Let AB be the cliff and O be the fixed point such that the angle of elevation of the cliff
from O is i.e., ∠AOB = θ. Let ∠AOC =¢ and OC = k metres. From C draw CD
and CE perpendiculars on AB and OA respectively. Then, ∠DCB = α Let h be the height of the cliff AB.
In ΔOCE we have

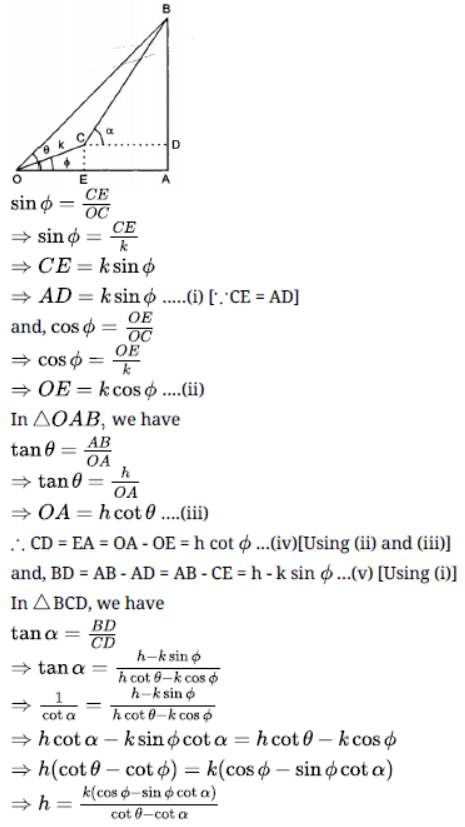
Question. A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.   
Solution.

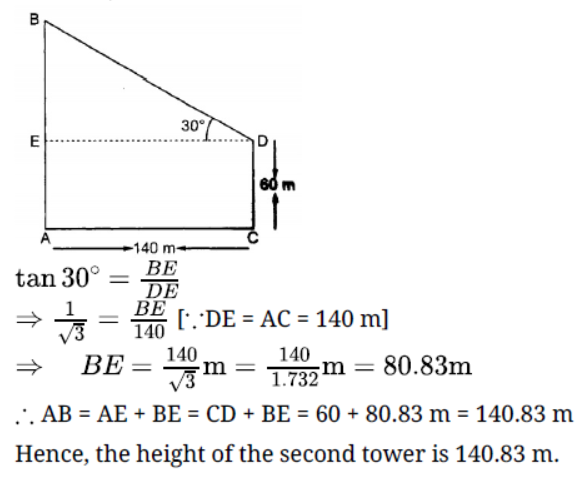
Question. The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower, when seen from the top of the second tower is 30°. If the height of the second tower is 60 m, find the height of the first tower.   
Solution. Let AB and CD be two towers of height h metres and 60 metres respectively such that
the distance AC between them is 140 m. The angle of elevation of top B of tower AB as
seen from D (top of tower CD) is 30°.
ΔDEB , we have

Question. At some time of the day the length of the shadow of a tower is equal to its height. Find the sun’s altitude at that time.   
given, the length of the shadow of a tower is equal to its height i.e. AB=BC In right ΔABC
Solution.

Mathematics Applications Of Trigonometry Worksheets for Class 10 as per CBSE NCERT pattern

Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 1 Mathematics Applications Of Trigonometry book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Applications Of Trigonometry for Class 1 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.

Benefits of Free Worksheets for Applications of Trigonometry Worksheet Class 10 Maths

1. You can improve understanding of your concepts if you solve NCERT Class 1 Mathematics Applications Of Trigonometry Worksheet,
2. These CBSE Class 1 Mathematics Applications Of Trigonometry worksheets can help you to understand the pattern of questions expected in Mathematics Applications Of Trigonometry exams.
3. All worksheets for Mathematics Applications Of Trigonometry Class 1 for NCERT have been organized in a manner to allow easy download in PDF format
4. Parents will be easily able to understand the worksheets and give them to kids to solve
5. Will help you to quickly revise all chapters of Class 1 Mathematics Applications Of Trigonometry textbook
6. CBSE Class 1 Mathematics Applications Of Trigonometry Workbook will surely help to improve knowledge of this subject

These Printable practice worksheets are available for free download for Class 1 Mathematics Applications Of Trigonometry. As the teachers have done extensive research for all topics and have then made these worksheets for you so that you can use them for your benefit and have also provided to you for each chapter in your ebook. The Chapter wise question bank and revision worksheets can be accessed free and anywhere. Go ahead and click on the links above to download free CBSE Class 1 Mathematics Applications Of Trigonometry Worksheets PDF.