Worksheets Chapter 1 Real Number Class 10 Mathematics

Students should refer to Worksheets Class 10 Mathematics Real Number Chapter 1 provided below with important questions and answers. These important questions with solutions for Chapter 1 Real Number have been prepared by expert teachers for Class 10 Mathematics based on the expected pattern of questions in the Class 10 exams. We have provided Worksheets for Class 10 Mathematics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.

Real Number Worksheets Class 10 Mathematics

VERY SHORT ANSWER TYPE QUESTIONS

Question. If a = xy² and b = x³y⁵ where x and y are prime numbers then LCM of (a, b) is _____ .
Ans. x³ × y⁵

Question. In the given factor tree find x and y

Ans. x = 35, y = 70

Question. Write the form in which every odd integer can be written taking t as variable.
Ans. 2t + 1

Question. What would be the value of n for which n²–1 is divisible by 8.
Ans. An odd integer

Question. If n is a natural number, then 25²ⁿ – 9²ⁿ is always divisible by :
(i) 16
(ii) 34
(iii) both 16 or 34
(iv) None of these
Ans. (i) 16

Question. Euclid’s division Lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy.
(a) 1 < r < b
(b) 0 < r ≤ b
(c) 0 ≤ r < b
(d) 0 < r < b
Ans. (c) 0 ≤ r < b

Question. A number N when divided by 16 gives the remainder 5 ______ is the remainder when the same number is divided by 8.
Ans. 5

Question. HCF of 3³ × 5⁴ and 3⁴ × 5² is ________ .
Ans. 3³ × 5²

Question. All decimal numbers are
(a) rational number
(b) irrational numbers
(c) real numbers
(d) integers
Ans. (c) real numbers

Question. Which of these numbers always end with the digits 6.
(a) 4ⁿ
(b) 2ⁿ
(c) 6ⁿ
(d) 8ⁿ
Ans. (c) 6ⁿ

SHORT ANSWER TYPE QUESTIONS-I

Question. A rational number in its decimal expansion is 327. 7081. What can you say about the prime factors of q, when this number is expressed in the form of p/q ? Give reasons.
Ans. Denominator is the multiple of 2’s and 5’s.

Question. What is the smallest number by which √5 – √2 is to be multiplied to make it a rational number? Also find the number so obtained?
Ans. √5 + √2 , 3

Question. If n is an odd integer then show that n² – 1 is divisible by 8.
Ans. Any +ve odd integer is of the form 4q + 1 or 4q + 3 for some integer q so if n = 4q + 1.
n2 – 1 = (4q + 1)²–1 = 16q² + 8q = 8q(2q + 1) ⇒ n² – 1 is divisible by 8.
If n = 4q + 3
n² – 1 =(4q + 3)² – 1 = 16q² + 24q + 8 = 8 (2q² + 3q + 1) ⇒ n² – 1 is divisible by 8.

Question. Use Euclid’s division algorithm to find the HCF of 16 and 28.
Ans. 4

Question. Find one rational and one irrational no between √3 and √5.
Ans. Rational number between √3 and √5 is √4, and irrational number between √3 and √5 is (√3+√5)/2.

Question. If HCF of 144 and 180 is expressed in the form 13m – 3, find the value of m.
Ans. By Euclid’s division lemma
180 = 144 × 1 + 36
144 = 36 × 4 + 0

HCF of 180 and 144 is 36.
13m – 3 = 36
13 m = 39
m = 3

SHORT ANSWER TYPE QUESTIONS-II

Question. In a seminar, the no. of participants in Hindi, English and Mathematics are 60, 84 and 108 respectively. Find the minimum number of rooms required if in each room the some the same number of participants are to be seated and all of the them being of the the same subject.
Ans. HCF of 60, 84 and 108 is 2² × 3 = 12 = No. of participants in each row.
No. of rooms required = Total number of participants/12
= (60+84+108)/12 = 21 rooms

Question. State fundamental theorem of Arithmetic. Is it possible that HCF and LCM of two numbers be 24 and 540 respectively. Justify your answer.
Ans. HCF = 24, LCM = 540
LCM/HCF = 540/24 = 22.5, not an integer.
Hence two numbers cannot have HCF and LCM as 24 and 540 respectively.

Question. If 105/(2³×5²×3^p×7^q) is a terminating decimal, what are the least possible values of p and q.
Ans. 0 and 1

Question. During a sale, colour pencils were being sold in the pack of 24 each and crayons in the pack of 32 each. If you want full packs of both and the same number of pencils and crayons, how many packets of each would you need to buy?
Ans. LCM of 24 and 32 is 96
96 crayons or 96/32 = 3 packs of crayons
96 pencils or 96/24 = 4 packs of pencils.

Question. Show that the cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3 for some integer m.
Ans. Let n be any psoitve integer. Then it is of the form 4q, 4q + 1, 4q + 2 and 4q + 3.
When n = 4q, n³ = 64q³ = 4 (16q³) = 4 m, where m = 16q³
When n = 4q + 1, n³ = (4q + 1)³ = 64q³ + 48q² + 12q + 1
= 4(16q³ + 12q² + 3q) + 1 = 4 m + 1.
where m = 16q³ + 12q² + 3q
Similarly discuss for n = 4q + 2 and 4q + 3.

Question. If 7560 = 2³ × 3^p × q × 7, find p and q.
Ans. p = 3 and q = 5

Question. Find the largest number that divides 31 and 99 leaving remainder 5 and 8 respectively.
Ans. Given number = 31 and 99
31 – 5 = 26 and 99 – 8 = 91
Prime factors of 26 = 2 × 13
91 = 7 × 13
HCF of (26, 91) = 13.
∴ 13 is the largest number which divides 31 and 99 leaving remainder 5 and 8 respectively.

Question. The HCF of 65 and 117 is expressible in the form 65 m – 117. Find the value of m. Also find the LCM of 65 and 117 using prime factorisation method.
Ans. HCF of 117 and 65 by Euclid division algorithm.
117 = 65 × 1 + 52
65 = 52 × 1 = 52
52 = 13 × 4 + 0
HCF (117, 52) = 13.
Given that 65 m – 117 = 13 ⇒ 65 m = 130 ⇒ m = 2.
LCM (65, 117) = 13 × 3² × 5 = 585

Question. Express the HCF of numbers 72 and 124 as a linear combination of 72 and 124.
Ans. HCF (124, 72) = 4
4 = 124 × 7 + 72 × (– 12), x = 7, y = – 12

Question. Show that there is no positive integer n for which √(n – 1) + √(n + 1) is rational.
Ans. Let √(n-1) + √(n+1) = p/q (1)q ≠ 0, p, q, co-prime.

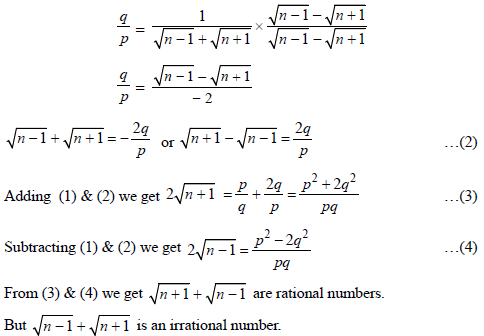
∴ These exist no positive integer n, for which √(n-1) + √(n+ 1) is rational.

Question. Using Euclid’s division algorithm, find the largest number that divides 1251, 9377 and 15628 leaving remainder 1, 2 and 3 respectively.
Ans. 1251 – 1 =1250, 9377 – 2 = 9375, 15628 – 3 = 15625
HCF of (15625, 9375) = 3125
HCF of (3125, 1250) = 625
⇒ HCF of (1250, 9375, 15625) = 625

Question. Show that square of any odd integer is of the form 4m + 1, for some integer m.
Ans. By Euclid’s division algorithm, we have a = bq + r, where 0 ≤ r < 4. On
putting b = 4 we get a = 4q + r where, r = 0, 1, 2, 3.
If r = 0, a = 4q which is even
If r = 1, a = 4q + 1 not divisible by 2
If r = 2, a = 4q + 2 = 2(2q + 1) which is even
If r = 3, a = 4q + 3 not divisible by 2.
So, for any +ve integer q, 4q + 1 and 4q + 3 are odd integers.
How, a² = (4q + 1)² = 16q² + 1 + 8q = 4(4q² + 2q) + 1 = 4m + 1
where m = 4q² + 2q similarly for 4q + 3.

Question. Three bells ring at intervals of 9, 12, 15 minutes respectively. If they start ringing together at a time, after how much time will they next ring together?
Ans. LCM of (9, 12, 15) = 180 minutes.

Question. Explain why: 7 × 11 × 13 × 15 + 15 is a composite number
Ans. 15 × (7 × 11 × 13 + 1) as it has more than two factors so it is composite number.

Question. On a morning walk, three persons steps off together and their steps measure 40 cm, 42 cm, and 45 cm respectively. What is the minimum distance each should walk, so that each can cover the same distance in complete steps?
Ans. LCM of 40, 42, 45 = 2520
Minimum distance each should walk 2520 cm.

Question. Show that either the number n, n + 2 and n + 4 are three consecutive odd numbers or 3 even numbers.
Ans. Let the number divisible by 3 is of the form 3k + r, r = 0, 1, 2
a = 3k, 3k + 1 or 3k + 2
(i) When a = 3k
n = 3k ⇒ n is divisible by 3.
n + 2 = 3k + 2 ⇒ n + 2 is not divisible by 3.
n + 4 = 3k + 4 = 3k + 3 + 1 = 3(k + 1) + 1 ⇒ n + 4 is not divisible by 3.
So, only one out of n, n + 2 and n + 4 is divisible by 3.
(ii) When a = 3k + 1
n = 3k + 1 ⇒ n is not divisible by 3.
n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1)
⇒ n + 2 is divisible by 3.
n + 4 = 3k + 1 + 4 = 3k + 5 = 3(k + 1) + 2
⇒ n + 2 is not divisible by 3.
So, only one out of n, n + 2 and n + 4 is divisible by 3.
Similarly do for a = 3k + 2.