Students should refer to Worksheets Class 12 Physics Wave Optics Chapter 10 provided below with important questions and answers. These important questions with solutions for Chapter 10 Wave Optics have been prepared by expert teachers for Class 12 Physics based on the expected pattern of questions in the Class 12 exams. We have provided Worksheets for Class 12 Physics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Wave Optics Worksheets Class 12 Physics
Question: In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In thiscase
(a) there shall be alternate interference patterns of red and blue
(b) there shall be an interference pattern for red distinct from that for blue
(c) there shall be no interference fringes
(d) there shall be an interference pattern for red mixing with one for blue
Answer:
C
Question: Yellow light of wavelength 6000 Å produces fringes of width 0.8 mm in Young’s double slit experiment. If the source is replaced by another monochromatic source of wavelength 7500 Å and the separation between the slits is doubled then the fringe width becomes
(a) 0.1 mm
(b) 0.5 mm
(c) 4.3 mm
(d) 1 mm
Answer:
B
Question: In Young’s double slit experiment the distance d between the slits S1 and S2 is 1 mm.
What should the width of each slit be so as to obtain 10 maxima of the double slit pattern within the central maximum of the single slit pattern?
(a) 0.9 mm
(b) 0.8 mm
(c) 0.2 mm
(d) 0.6 mm
Answer:
C
Question: Two sources of light of wavelength 2500 Å and 3500 Å are used in Young’s double slit experiment simultaneously. Which orders of fringes of two wavelength patterns coincide?
(a) 3rd order of 1st source and 5th of the 2nd
(b) 7th order of 1st and 5th order of 2nd
(c) 5th order of 1st and 3rd order of 2nd
(d) 5th order of 1st and 7th order of 2nd
Answer:
B
Question: When interference of light takes place
(a) energy is created in the region of maximum intensity
(b) energy is destroyed in the region of maximum intensity
(c) conservation of energy holds good and energy is redistributed
(d) conservation of energy does not hold good
Answer:
C
Question: The idea of secondary wavelets for the propagation of a wave was first given by
(a) Newton
(b) Huygens
(c) Maxwell
(d) Fresnel
Answer:
B
Question: Which of the following is the path difference for distructive interference ?

Answer:
B
Question: In a Young’s double slit experiment, (slit distance d) monochromatic light of wavelength l is used and the fringe pattern observed at a distance D from the slits. The angular position of the bright fringes are
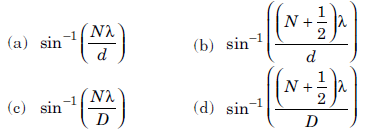
Answer:
A
Question:The phenomena which is not explained by Huygens construction of wavefront
(a) reflection
(b) diffraction
(c) refraction
(d) origin of spectra
Answer:
D
Question: A narrow slit of width 2 mm is illuminated by monochromatic light of wavelength 500 nm.
The distance between the first minima on either side on a screen at a distance of 1 m is
(a) 5 mm
(b) 0.5 mm
(c) 1 mm
(d) 10 mm
Answer:
B
Question: For what distance is ray optics a good approximation when the aperture is 4 mm wide and the wavelength is 500 nm?
(a) 22 m
(b) 32 m
(c) 42 m
(d) 52 m
Answer:
B
Question: A slit of width d is illuminated by white light.
The first minimum for red light (l = 6500 Å) will fall at q = 30° when d will be
(a) 3200 Å
(b) 6.5 × 10–4 mm
(c) 1.3 micron
(d) 2.6 × 10–4 cm C
Answer:
C
Question: The two coherent sources with intensity ratio b produce interference. The fringe visibility will be

Answer:
A
Question: In a Young’s double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2 = θ andλ is the wavelength,the fringe width will be

Answer:
A
Question: Wavefront is the locus of all points, where the particles of the medium vibrate with the same
(a) phase
(b) amplitude
(c) frequency
(d) period
Answer:
A
Question: Young’s experiment is performed with light of wavelength 6000 Å wherein 16 fringes occupy a certain region on the screen.
If 24 fringes occupy the same region with another light, of wavelength λ, then λ, is
(a) 6000 Å
(b) 4500 Å
(c) 5000 Å
(d) 4000 Å
Answer:
D
Question: Light from two coherent sources of the same amplitude A and wavelength λ illuminates the screen. The intensity of the central maximum is I0. If the sources were incoherent, the intensity at the same point will be
(a) 4I0
(b) 2I0
(c) I0
(d) I0/2
Answer:
D
Question: In a Young’s double slit experiment, the angular width of a fringe formed on a distant screen is 1°. The slit separation is 0.01 mm. The wavelength of the light is
(a) 0.174 nm
(b) 0.174 Å
(c) 0.174 μm
(d) 0.174 × 10–4 m
Answer:
C
Assertion & Reasoning Based MCQs
two statements are given-one labelled Assertion (A) and the other labelled Reason (R).
Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
Question: Assertion (A) : Interference obeys the law of conservation of energy.
Reason (R) : The energy is redistributed in case of interference.
Answer:
A
Question: Assertion (A) : We cannot get diffraction pattern from a wide slit illuminated by monochromatic light.
Reason (R) : In diffraction pattern, all the bright bands are not of the same intensity.
Answer:
B
Question: Assertion (A) : One of the condition for interference is that the two source should be very narrow.
Reason (R) : One broad source is equal to large number of narrow sources.
Answer:
A
Question: Assertion (A) : The maximum intensity in interference pattern is four times the intensity due to each slit.
Reason (R): Intensity is directly proportional to square of amplitude.
Answer:
B
Question: Assertion (A) : When a light wave travels from a rarer to a denser medium, it loses speed.
The reduction in speed imply a reduction in energy carried by the light wave.
Reason (R) : The energy of a wave is proportional to velocity of wave.
Answer:
D
Very Short Answer Type Questions
Question: What is the shape of the wavefront on earth for sunlight?
Answer : There would be spherical wave front on earth for sunlight which is treated as point source, but radius is very large as compared to radius of earth, so it is almost a plane wavefront
Question: In double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits?
Answer:
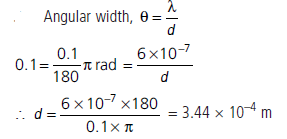
Question:If one of the slits in Young’s double slit experiment is fully closed, the new pattern has ______ central maximum in angular size.
Answer : In young’s double slit experiment, if one slit is fully closed, the new pattern has larger central maximum in angular size.
Question: Two slits are made one millimetre apart and the screen is placed one metre away. What is the fringe separation when blue-green light of wavelength 500 nm is used?
Answer:
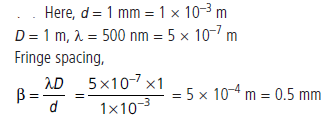
Question: Why is the diffraction of sound waves more evident in daily experience than that of light wave?
Answer : The diffraction effect is more pronounce if the size of the aperture or the obstacle is of the order of wavelength of wave.
As wavelength of light (≃ 10–6 m) is much more smaller than size of object around us so diffraction of light is not easily seen but sound wave has large wavelength (15 mm < λ< 15 m), they get easily diffracted by objects around us.
Short Answer Type Questions
Question:White coherent light (400 nm-700 nm) is sent through the slits of a YDSE, the separation between the slits is 0.5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1 mm away (along the width of the fringes) from the central line. Which wavelength will be absent in the light coming from the hole?
Answer:

Question: A beam of light consisting of two wavelengths, 6500 Å and 5200 Å is used to obtain slit experiment (1 Å = 10–10 m). The distance between the slits is 2.0 mm and the distance between the plane of the slits and the screen is 120 cm.
(i) Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 6500 Å.
(ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Answer:
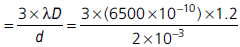
= 0.117cm = 1.17mm
(ii) Say mth bright fringe of 6500 Å coincides with nth bright fringe of 5200 Å
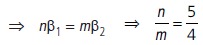
Hence, for least distance, 5th bright fringe of 5200 Å coincides with 4th bright fringe of 6500 Å.
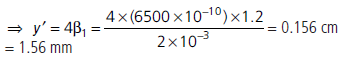
Question: (a) Two monochromatic waves emanating from two coherent sources have the displacements represented by y1 = a cos ωt and y2 = a cos (ωt + Φ) where f is the phase difference between the two displacements. Show that the resultant intensity at a point due to their superposition is given by I = 4 I0 cos2 Φ2, where I0 = a2.
(b) Hence obtain the conditions for constructive and destructive interference.
Answer:(a) y1 = a cos wt, y2 = a cos (wt + f)
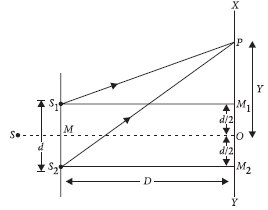
where Φ is phase difference between them. Resultant displacement at point P will be,
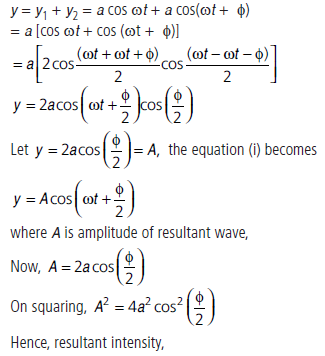
Question: (a) Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence obtain the conditions for the angular width of secondary maxima and secondary minima.
(b) Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 ×10–6 m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
Answer:
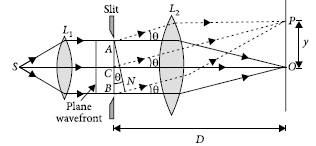
Consider a set of parallel rays from a lens L1 falling on a slit, form a plane wavefront. According to Huygens principle, each point on the unblocked point of plane wavefront AB sends out secondary wavelets in all directions. The secondary waves from points equidistant from the centre C of the slit lying in the portion CA and CB of the wavefront travel the same distance in reaching at O and hence the path difference between them is zero. These secondary waves reinforce each other, resulting maximum intensity at point O. Position of secondary minima : The secondary waves travelling in the direction making an angle q with CO, will reach a point P on the screen. The intensity at P will depend on the path difference between the secondary waves emitted from the corresponding points of the wavefront. The wavelets from points A and B will have a path difference equal to BN. If this path difference is l, then P will be a point of minimum intensity. This is because the whole wavefront can be considered to be divided into two equal halves CA and CB. If the path difference between secondary waves from A and B is l, then the path difference between secondary waves from A and C will be l/2 and also the path difference between secondary waves from B and C will again be l/2. Also for every point in the upper half AC, there is a corresponding point in the lower half CB for which the path difference between secondary waves reaching P is l/2. Thus, at P destructive interference will take place. From the right-angled DANB given in figure
BN = AB sin Θ
BN = a sin Θ
Suppose BN = λ and Θ = Θ1
∴ λ = a sin θ1
sinθ1 = λ/a
Such a point on the screen will be the position of the first secondary minimum.
If BN = 2λ and θ= θ2, then,
2λ = a sin θ2
sinθ2=2λ/ a
Question: Why cannot two independent monochromatic sources produce sustained interference pattern?
Deduce, with the help of Young’s arrangement to produce interference pattern, an expression for the fringe width.
Answer: (i) Two independent monochromatic sources cannot produce sustained interference pattern because the phase difference between the light waves from two independent sources keeps on changing continuously.
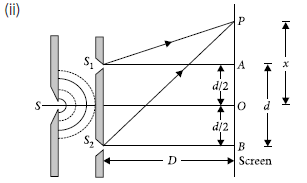
Consider a point P on the screen at distance x from the centre O. The nature of the interference at the point P depends on path difference,
p = S2P – S1P

p=xd/D= = (2n −1) λ/2
or x=(2n-1)Dλ/2d where n = 1, 2, 3
Width of a dark fringe = Separation between two
consecutive bright fringes
=xn-xn-1=nDλ /d-(n-1)Dλ /d=Dλ/d
Width of bright fringe = Separation between two
consecutive dark fringes
=x’n-x’n-1=(2n-1)Dλ/2d-[2(n-1)-1]Dλ/2d=Dλ /d
Clearly, both the bright and dark fringes are of equal width.
Hence the expression for the fringe width in Young’s double slit experiment can be written as
β=Dλ /d
Question: Consider a two slit interference arrangements such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
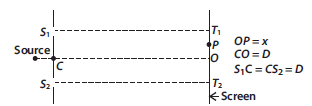
Answer: From diagram

Question: The YDSE set-up is shown. On the lower slit a slab of thickness 0.1 mm and refractive index 3/2 is placed. Find
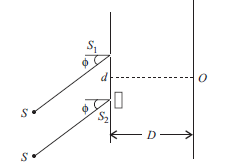
(i) Position of central maxima
(ii) Order of maxima at O and how many fringes will cross O if slab is removed? l = 5000 Å, d = 50 ×× 10–4 cm, f = 30°, D = 2 m
Answer:

Question: A plane wavefront propagating in a medium of refractive index ‘m1’ is incident on a plane surface making the angle of incidence i as shown in the figure. It enters into a medium of refraction of refractive index ‘μ2’ (μ2 > μ1). Use Huygens’ construction of secondary wavelets to trace the propagation of the refracted wavefront.
Hence verify Snell’s law of refraction.
Answer: Snell’s law of refraction : Let P1P2 represents the surface separating medium 1 and medium 2 as shown in figure.
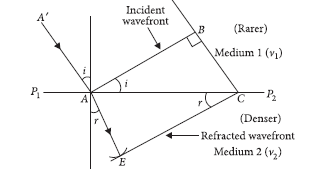
Let v1 and v2 represents the speed of light in medium 1 and medium 2 respectively. We assume a plane wavefront AB propagating in the direction A′A incident on the interface at an angle i. Let t be the time taken by the wavefront to travel the distance BC.
∴ BC = v1t [… distance = speed × time]
In order to determine the shape of the refracted wavefront, we draw a sphere of radius v2t from the point A in the second medium (the speed of the wave in second medium is v2).
Let CE represents a tangent plane drawn from the point C.
Then

Question: The figure shows a modified Young’s double slit experimental set-up. Here SS2 – SS1 = λ/4.
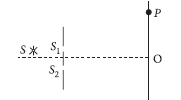
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
Answer: (a) Given :SS2 SS1=λ/4
Now path difference between the two waves from slit S1 and S2 on reaching point P on screen is
Δx = (SS2 + S2P) – (SS1 + S1P)
or Δx = (SS2 – SS1) + (S2P – S1P)
orΔx λ/4+yd/D,, where d is the slits separation
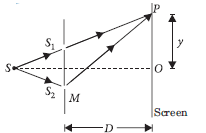
For constructive interference at point P, path difference
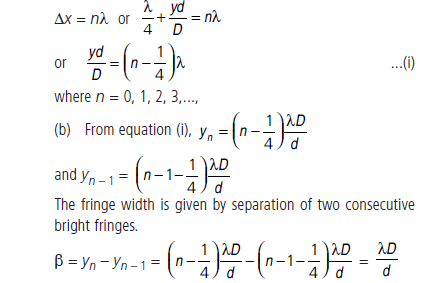
Question: (a) If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
(b) What kind of fringes do you expect to observe if white light is used instead of onochromatic light?
Answer:
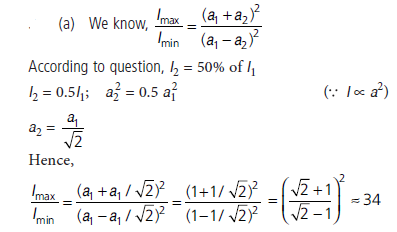
(b) The central fringes are white. On the either side of the central white fringe the coloured bands (few coloured maxima and minima) will appear. This is because fringes of different colours overlap.
Question: In a YDSE, D = 1 m, d = 1 mm, and l = 1/2 mm.
(i) Find the distance between the first and central maxima on the screen.
(ii) Find the number of maximum and minimum obtained on the screen.
Answer:

Case Based MCQs
Diffraction
The phenomenon of bending of light around the sharp corners and the spreading of light within the geometrical shadow of the opaque obstacles is called diffraction of light. The light thus deviates from its linear path. The deviation becomes much more pronounced, when the dimensions of the aperture or the obstacle are comparable to the wavelength of light.
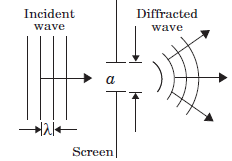
Question: For a diffraction from a single slit, the intensity of the central point is
(a) infinite
(b) finite and same magnitude as the surrounding maxima
(c) finite but much larger than the surrounding maxima
(d) finite and substantially smaller than the surrounding maxima
Answer:
C
Question: In diffraction from a single slit the angular width of the central maxima does not depends on
(a) l of light used
(b) width of slit
(c) distance of slits from the screen
(d) ratio ofλand slit width
Answer:
C
Question: In a single diffraction pattern observed on a screen placed at D metre distance from the slit of width d metre, the ratio of the width of the central maxima to the width of other secondary maxima is
(a) 2 : 1
(b) 1 : 2
(c) 1 : 1
(d) 3 : 1
Answer:
A
Young’s Double Slit Experiment
A narrow tube is bent in the form of a circle of radius R, as shown in figure. Two small holes S and D are made in the tube at the positions at right angle to each other. A source placed at S generates a wave of intensity I0 which is equally divided into two parts: one part travels along the longer path, while the other travels along the shorter path. Both the waves meet at point D where a detector is placed.
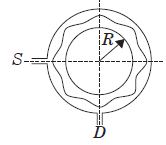
Question: If a maxima is formed at a detector, then the magnitude of wavelength l of the wave produced is given by
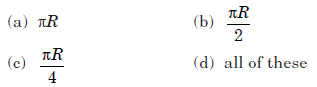
Answer:
D
Question: In a Young’s double slit experiment, the intensity at a point where the path difference is l/6 (l – wavelength of the light) is I. If I0 denotes the maximum intensity, then I/I0 is equal to

Answer:
D
Question: The maximum intensity produced at D is given by
(a) 4I0
(b) 2I0
(c) I0
(d) 3I0
Answer:
B
Question: Two identical light waves, propagating in the same direction, have a phase difference d. After they superpose the intensity of the resulting wave will be proportional to
(a) cosd
(b) cos(d/2)
(c) cos2(d/2)
(d) cos2d
Answer:
C
