Students should refer to Worksheets Class 12 Physics Atoms Chapter 12 provided below with important questions and answers. These important questions with solutions for Chapter 12 Atoms have been prepared by expert teachers for Class 12 Physics based on the expected pattern of questions in the Class 12 exams. We have provided Worksheets for Class 12 Physics for all chapters on our website. You should carefully learn all the important examinations questions provided below as they will help you to get better marks in your class tests and exams.
Atoms Worksheets Class 12 Physics
Question: From quantisation of angular momentum, one gets for hydrogen atom, the radius of the nth orbit as rn[n2/me][h/2π]2[4π2εo/e2]
For a hydrogen like atom of atomic number Z,
(a) the radius of the first orbit will be the same
(b) rn will be greater for larger Z values
(c) rn will be smaller for larger Z values
(d) none of these.
Answer:
C
Question: In the Bohr model of the hydrogen atom, the lowest orbit corresponds to
(a) infinite energy
(b) maximum energy
(c) minimum energy
(d) zero energy.
Answer:
C
Question: The binding energy of an electron in the ground state of He is equal to 24.6 eV. The energy required to remove both the electrons is
(a) 49.2 eV
(b) 54.4 eV
(c) 79 eV
(d) 108.8 eV
Answer:
C
Question: In an experiment on a-particle scattering, a-particles are directed towards a gold foil and detectors are placed in position P,Q and R. What is the distribution of a-particles as recorded at P, Q and R ?
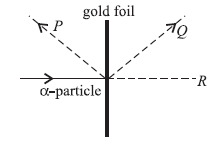
P Q R
(a) all none none
(b) none none all
(c) a few some most
(d) most some a few
Answer:
C
Question: Out of the following which one is not a possible energy for a photon to be emitted by hydrogen atom according to Bohr’s atomic model?
(a) 0.65 eV
(b) 1.9 eV
(c) 11.1 eV
(d) 13.6 eV
Answer:
C
Question: Bohr’s basic idea of discrete energy levels in atoms and the process of emission of photons from the higher levels to lower levels was experimentally confirmed by experiments performed by
(a) Michelson–Morley
(b) Millikan
(c) Joule
(d) Franck and Hertz
Answer:
D
Question: The diagram shows the energy levels for an electron in a certain atom.
Which transition shown represents the emission of a photon with the most energy ?
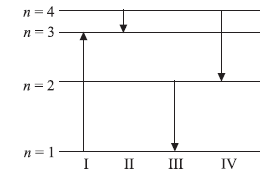
(a) I
(b) II
(c) III
(d) IV
Answer:
C
Question: The ratio of the speed of the electron in the ground state of hydrogen atom to the speed of light in vacuum is
(a)
1/2
(b)2/237
(c)1/137
(d)1/237
Answer:
C
Question: If u1 is the frequency of the series limit of Lyman series, u2 is the frequency of the first line of Lyman series and u3 is the frequency of the series limit of the Balmer series, then
(a)v1 –v2 = u3
(b) v1 = v2 – v3
(c)1/ v2=1/v1+1/v3
(d)1/v1=1/ 1/v2+1/v3
Answer:
A
Question: Suppose an electron is attracted towards the origin by a force k/r, where k is a constant and r is the distance of the electron from the origin. By applying Bohr model to this system, the radius of nth orbit of the electron is found to be rn and the kinetic energy of the electron is found to be Tn. Then which of the following is true?
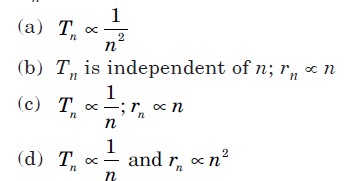
Answer:
B
Question: The first line of the Lyman series in a hydrogen spectrum has a wavelength of 1210 Å.
The corresponding line of a hydrogen-like atom of Z = 11 is equal to
(a) 4000 Å
(b) 100 Å
(c) 40 Å
(d) 10 Å
Answer:
D
Question: The excitation energy of Lyman last line is
(a) the same as ionisation energy
(b) the same as the last absorption line in Lyman series
(c) both (a) and (b)
(c) different from (a) and (b)
Answer:
C
Question:(a) equal to one-fourth the circumference of the first orbit
(b) equal to half the circumference of first orbit
(c) equal to twice the circumference of first orbit
(d) equal to the circumference of the first orbit.
Answer:
D
Question: The electric current I created by the electron in the ground state of H atom using Bohr model in terms of Bohr radius (a0) and velocity of electron in first orbit v0 is
(a) ev0/2πao
(b) 2πa/evo
(c) 2πa/vo
(d) vo/2πa
Answer:
A
Question: If the radius of inner most electronic orbit of a hydrogen atom is 5.3 × 10–11 m, then the radii of n = 2 orbit is
(a) 1.12 Å
(b) 2.12 Å
(c) 3.22 Å
(d) 4.54 Å
Answer:
B
Question: If the wavelength of the first line of the Balmer series of hydrogen is 6561 Å, the wavelength of the second line of the series should be
(a) 13122 Å
(b) 3280 Å
(c) 4860 Å
(d) 2187 Å
Answer:
C
Question: If muonic hydrogen atom is an atom in which a negatively charged muon (m) of mass about 207 me revolves around a proton, then first Bohr radius of this atom is (re = 0.53 × 10–10 m)
(a) 2.56 × 10–10 m
(b) 2.56 × 10–11 m
(c) 2.56 × 10–12 m
(d) 2.56 × 10–13 m
Answer:
D
Question: An electron is revolving in the nth orbit of radius 4.2 Å, then the value of n is (r1 = 0.529 Å)
(a) 4
(b) 5
(c) 6
(d) 3
Answer:
D
Question: A hydrogen atom initially in the ground level absorbs a photon and is excited to n = 4 level then the wavelength of photon is
(a) 790 Å
(b) 870 Å
(c) 970 Å
(d) 1070 Å
Answer:
C
Question: The wavelength limit present in the Pfund series is (R = 1.097 × 107 m–1)
(a) 1572 nm
(b) 1898 nm
(c) 2278 nm
(d) 2535 nm
Answer:
C
Assertion & Reasoning Based MCQs
Two statements are given-one labelled Assertion (A) and the other labelled Reason (R).
Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is NOT the correct explanation of A
(c) A is true but R is false
(d) A is false and R is also false
Question: Assertion (A) : According to classical theory, the proposed path of an electron in Rutherford atom model will be circular.
Reason (R) : According to electromagnetic theory an accelerated particle continuously emits radiation.
Answer:
B
Question: Assertion (A) : The force of repulsion between atomic nucleus and a-particle varies with distance according to inverse square law.
Reason (R) : Rutherford did a-particle scattering experiment.
Answer:
B
Question: Assertion (A) : Electrons in the atom are held due to coulomb forces.
Reason (R) : The atom is stable only because the centripetal force due to Coulomb’s law is balanced by the centrifugal force.
Answer:
C
Question: Assertion (A) : Total energy of revolving electron in any stationary orbit is negative.
Reason (R) : Energy is a scalar quantity. It can have positive or negative value.
Answer:
B
Question: Assertion (A) : Between any two given energy levels, the number of absorption transitions is always less than the number of emission transitions.
Reason (R) : Absorption transitions start from the lowest energy level only and may end at any higher energy level. But emission transitions may start from any higher energy level and end at any energy level below it.
Answer:
A
Question: Assertion (A) : For the scattering of a-particlesat large angles, only the nucleus of the atom is responsible.
Reason (R) : Nucleus is very heavy in comparison to electrons.
Answer:
A
Question: Assertion (A) : Balmer series lies in the visible region of electromagnetic spectrum.
Reason (R) : 1/ λ=R[1/22-1/K2,where K = 3, 4,5, …
Answer:
B
Question: Assertion (A) : Fraunhofer lines are observed in the spectrum of the sun.
Reason (R) : The different elements have different spectra.
Answer:
B
Very Short Answer Type Questions
Question: Calculate the shortest wavelength of the Brackett series and state to which part of the electromagnetic spectrum does it belong.
Answer: The shortest wavelength of Brackett series is given as
1/λ=1.097×107[1/42-1/∞2]=1.097×107/16.
⇒ λ = 1.4585 × 10–6 m
This wavelength lies in the infrared region of electromagnetic spectrum.
Question: What is the wavelength of the electronic de Broglie wave in the 3rd orbit of hydrogen?
Answer:
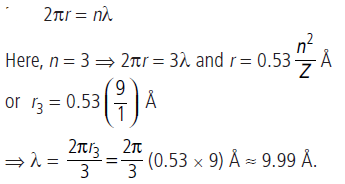
Question: Find the radius of the ground state orbit of hydrogen atom.
Answer: rn=n2h2/4π2mekze2=n2/z(0.053nm)
For our case, n = 1 and Z = 2, and the result is r1 = 0.027 nm.
Question: Find the wavelength of the IInd line of Balmer series.
Answer:
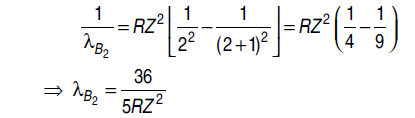
Question: Find the speed in the ground state
Answer:v=ze2/2εonh=c/137[Z/n]m/s
Here n = 1, Z = 2, v1 = 2c/137m/s.
Short Answer Type Questions
Question: An electron in the hydrogen atom makes a transition from n = 2 energy state to the ground state (corresponding to n = 1). Find the wavelength and frequency of the emitted photon.
Answer:

Question: Use the Bohr ’s model to estimate the wavelength of the Kα line in the kα-ray spectrum of platinum (Z = 78).
Answer:
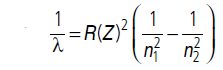
For characteristic X-rays, we replace Z by Z – a or (Z – 1)
here. For Kα, the electron jumps to the K-shell, hence,n1 = 1 and n2 =2.
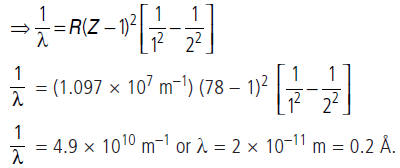
Question: Find the number of unique radiations that can be emitted for a sample of hydrogen atoms excited to the nth level.
Answer: The first excited level is 2nd line.
From the 2nd level electron can go to level 1 ⇒ one radiation
3rd level electron can go to levels 1, 2 ⇒ three radiations
4th level electron can go to levels 1, 2, 3 ⇒ six radiations
nth level electron can go to levels 1, 2, 3, …(n – 1)
∴ Total number of radiations
= 1 + 2 + …… + (n – 1) .n /2
Question: If Bohr’s quantisation postulate (angular momentum = nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantisation of orbits of planets around the sun?
Answer: Angular momentum mvr n=h /2π associated with planetary motion are incomparably large relative to h.
For example angular momentum of earth in its orbital motion is of the order of 1070 h/2π .
For such large value of n, the difference in successive energies and angular momenta of the quantised levels of the Bohr model are so small that one can predict the energy level continuous.
Question:Calculate the shortest wavelength in the Balmer series of hydrogen atom. In which region (infrared), visible, ultraviolet of hydrogen spectrum does this wavelength lie?
Answer: Wavelength (l) of Balmer series is given by
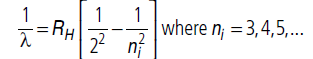
For shortest wavelength, when transition of electrons take place from ni = ∞ to nf = 2 orbit, wavelength of emitted photon is shortest.
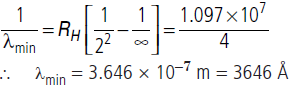
This wavelength lies in visible region of electromagnetic spectrum.
Question:The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10–11 m. What are the radii of the n = 2 and n = 3 orbits?
Answer: Radius of innermost electron r=n2h2εo/πme2
For n = 1, r1 = h2ε0/πme2= 5.3 × 10-11 m
For n = 2, r2 = (2)2 r1 = 2.12 × 10–10 m
For n = 3, r3 = (3)2 r1 = 4.77 × 10–10 m.
Question: The value of ground state energy of hydrogen atom is –13.6 eV.
(i) Find the energy required to move an electron from the ground state to the first excited state of the atom.
(ii) Determine (a) the kinetic energy and (b) orbital radius in the first excited state of the atom.
Answer: (Given the value of Bohr radius = 0.53 Å).
∴En=-13.6/n2eV
Energy of the photon emitted during a transition of the electron from the first excited state to its ground state is,
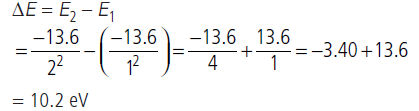
This transition lies in the region of Lyman series.
(ii) (a) The energy levels of H-atom are given by
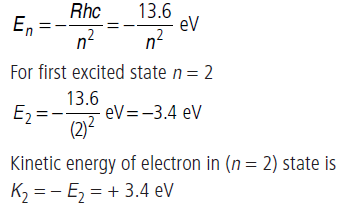
(b) Radius in the first excited state
r1 = (2)2 (0.53) Å
r1 = 2.12 Å
Question: Direction : Read the following passage and answer the questions given below.
In 1911, Rutherford, along with his assistants, H. Geiger and E. Marsden, performed the alpha
particle scattering experiment. H. Geiger and E. Marsden took radioactive source (214 83Bi) for a-particles. A collimated beam of α-pacles of energy 5.5 MeV was allowed to fall on 2.1 × 10–7 m thick gold foil. Observations of this experiment are as follows
(I) Most of the a-particles passed through the foil without deflection.
(II) Only about 0.14% of the incident a-particles scattered by more than 1°.
(III) Only about one a-particle in every 8000 a-particles deflected by more than 90°
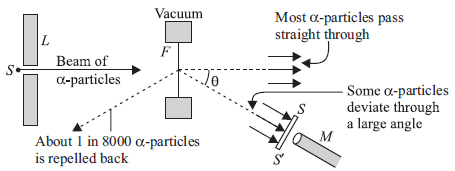
(i) Gold foil used in Geiger-Marsden experiment is about 10–8 m thick. What does it ensures?
(ii) On which factor, the trajectory traced by an a-particle depends?
(iii) In Rutherford scattering experiment the fact that only a small fraction of the number of incident particles rebound back. What it indicates?
Answer: (i) As the gold foil is very thin, it can be assumed that a-particles will suffer not more than one scattering during their passage through it. Therefore, computation of the trajectory of an a-particle scattered by a single nucleus is enough.
(ii) Trajectory of a-particles depends on impact parameter which is the perpendicular distance of the initial velocity vector of the a particles from the centre of the nucleus. For small impact parameter, a particle close to the nucleus suffers larger scattering.
(iii) In case of head-on-collision, the impact parameter is minimum and the a-particle rebounds back. So, the fact that only a small fraction of the number of incident particles rebound back indicates that the number of a-particles undergoing head-on collision is small. This in turn implies that the mass of the atom is concentrated in a small volume.
Question: The photons from Balmer series in hydrogen spectrum having wavelength between 450 nm to 700 nm are incident on a metal surface of work function 2 eV. Find the maximum kinetic energy of one photoelectron.
Answer: Wavelengths corresponding to minimum wavelength (λmin) or maximum energy will emit photoelectrons having maximum kinetic energy.
Wavelengths belonging to Balmer series and lying in the given range (450 nm to 750 nm) corresponds to transition from (n = 4 to n = 2). Here,

Question: A small particle of mass m moves in such a way that the potential energy
U = ar2 where a is a constant and r is the distance of the particle from the origin. Assuming Bohr’s model of quantisation of angular momentum for circular orbits, find the radius of nth allowed orbit.
Answer: The force at a distance r is
F =-dU/dr=− 2ar
Suppose r be the radius of nth orbit. The necessary centripetal force is provided by the above force. Thus,Further, the quantisation of angular momentum gives,mv2/r=2ar ..(i)
Further, the quantisation of angular momentum gives,
mvr=nh = 2π …(ii)
Solving, equations (i) and (ii) for r, we get r =[n2h2/8amπ 2]1/4
Question: A particle known as μ-meson, has a charge equal to that of an electron and mass 208 times the mass of the electron. It moves in a circular orbit around a nucleus of charge +3e. Take the mass of the nucleus to be infinite. Assuming that the Bohr’s model is applicable to this system,(i) derive an expression for the radius of the nth Bohr orbit,(ii) find the value of n for which the radius of the orbit is approximately the same as that of the first Bohr orbit for a hydrogen atom.
Answer:

Question: Positronium is just like a H-atom with the proton replaced by the positively charged antiparticle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium?
Answer: According to Bohr’s formula,
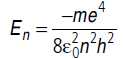
where m is called reduced mass.
In case of hydrogen, m = me = mass of electron.
For positronium,
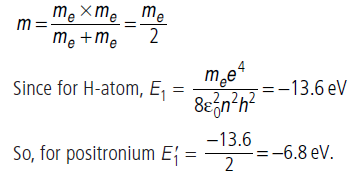
Question: A gas of hydrogen like atoms can absorb radiations of 68 eV. Consequently, the atoms emit radiations of only three different wavelength. All the wavelengths are equal or smaller than that of the absorbed photon.
(i) Determine the initial state of the gas atoms.
(ii) Identify the gas atoms.
(iii) Find the minimum wavelength of the emitted radiations.
Answer: (i) n(n − ) = 1/2=3 ∴ n = 3
i.e. after excitation atom jumps to second excited state.
Hence, nf = 3. So ni can be 1 or 2.
If ni = 1 then energy emitted is either equal to, greater than or
less than the energy absorbed. Hence, the emitted wavelength is either equal to, less than or greater than the absorbed wavelength.
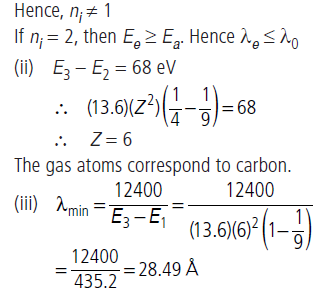
Long Answer Type Questions
Question: Using Bohr ’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number ni) to the lower state, (nf). When electron in hydrogen atom jumps from energy state ni = 4 to nf = 3, 2, 1. Identify the spectral series to which the emission lines belong.
Answer:

When electron in hydrogen atom jumps from energy state ni = 4 to nf = 3, 2, 1, the Paschen, Balmer and Lyman spectral series are found.
Question: The first four spectral lines in the Lyman series of a H-atom are λ = 1218 Å, 1028 Å, 974.3 Å
and 951.4 Å. If instead of Hydrogen, we consider Deuterium, calculate the shift in the wavelength of these lines.
Answer: Let μH and μD are the reduced masses of electron for hydrogen and deuterium respectively.
Case Based MCQs
Second Postulate of Bohr’s Theory
Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr, this electron moves in a stationary orbit. When this electron is in the stationary orbit, it emits no electromagnetic radiation. The angular momentum of the electron is quantized, i.e., mvr = (nh/2p), where m = mass of the electron, v = velocity of the electron in the orbit, r = radius of the orbit and n = 1, 2, 3, …. When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is l, we find that 1/λ=R[1/j2-1/k2] , where R is Rydberg’s constant.
On a different planet, the hydrogen atom’s structure was somewhat different from ours. The angular momentum of electron was P = 2n(h/2p), i.e., an even multiple of (h/2π).
Question: In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state.
The velocity of electron in this state on the other planet should be
(a) v0
(b) v0/2
(c) v0/4
(d) v0/8
Answer:
B
Question: The minimum permissible radius of the orbit will be
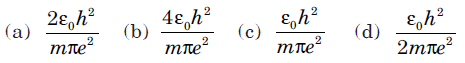
Answer:
B
Question: In Bohr’s model of hydrogen atom, let PE represent potential energy and TE the total energy. In going to a higher orbit
(a) PE increases, TE decreases
(b) PE decreases, TE increases
(c) PE increases, TE increases
(d) PE decreases, TE decreases
Answer:
C
Question: Check the correctness of the following statements about the Bohr model of hydrogen atom.
(i) The acceleration of the electron in n = 2 orbit is more than that in n = 1 orbit.
(ii) The angular momentum of the electron in n = 2 orbit is more than that in n = 1 orbit.
(iii) The kinetic energy of the electron in n = 2 orbit is less than that in n = 1 orbit.
(a) Only (iii) and (i) are correct.
(b) Only (i) and (ii) are correct.
(c) Only (ii) and (iii) are correct.
(d) All the statements are correct.
Answer:
C
